БАЙЕСОВСКИЕ ПРОЦЕДУРЫ РАСПОЗНАВАНИЯ ОБРАЗОВ

Глава 4. МЕТОДЫ КЛАССИФИКАЦИИ И РАСПОЗНАВАНИЯ ОБРАЗОВ, ИСПОЛЬЗУЮЩИЕ ЕВКЛИДОВЫ ПРОСТРАНСТВА ОПИСАНИЙ

Рассмотрим основные методы параллельного распознавания образов при использовании для описания классифицируемых объектов совокупности измерений, определяющих оси евклидова пространства, и их представления точками в этом пространстве.

Предположим, что существует известное множество C = {C_j}, состоящее из k взаимно исключающих классов объектов. Каждый объект представляется набором результатов измерений, называемым его описанием. Одно измерение – это точка на некоторой шкале, а совокупность шкал, в свою очередь, определяет пространство описаний D. Таким образом, описание объекта – это точка x в пространстве D.

Процедура классификации образов относит образ к классу объектов С_i тогда и только тогда, когда его описание попадает в область R_i пространства D, соответствующую этому классу. Такая процедура классификации образов корректна, если объект и в самом деле относится к классу i.

Процедура распознавания образов определяет области {R_i} путем исследования описаний множества S объектов, про которые известно, к каким классам они на самом деле принадлежат. Итак, S будет выборкой, с которой работает процедура распознавания образов.

БАЙЕСОВСКИЕ ПРОЦЕДУРЫ РАСПОЗНАВАНИЯ ОБРАЗОВ

Процедуры распознавания зависят от понятия расстояния между двумя точками в пространстве описаний D. Если в пространстве D расстояние между точками, являющимися описаниями двух объектов, достаточно мало, то делается заключение, что эти объекты принадлежат одному классу. Такой подход справедлив для большинства физических шкал, таких, как рост и вес, но менее пригоден, если описание основано на присутствии или отсутствии каких-то признаков. Покажем, какие именно свойства самих измерений вытекают из предположения о существовании расстояния.

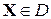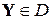В m-мерном пространстве D два объекта описываются двумя точками: и , которые представляют собой m-мерные вектора
(x₁, …, x_m) и (y₁, …, y_m), соответственно, при этом расстояние между нимив D оценивается выражением

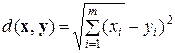. (23)

Таким образом, расстояние между двумя точками зависит от их относительного, а не от абсолютного расположения в пространстве D, т. е. точки X, Y удалены друг от друга на то же расстояние, что и точки 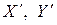, если

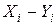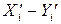= для всех «i».

Шкалу, позволяющую сравнивать отдельные измерения, иногда называют шкалой интервалов. Примерами таких шкал являются шкалы времени, веса и роста. Шкалы интервалов инвариантны относительно линейных преобразований, а параметры пространства описаний D связаны с параметрами нового пространства 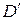формулой

.

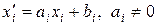Существуют шкалы, не обладающие свойством шкалы интервалов. Например, твердость обычно относят к шкале порядка, поскольку ее можно использовать для того, чтобы приписать объектам числа, отражающие лишь некоторое упорядочение, а не свойство равных интервалов.

В абсолютных шкалах помимо интервального свойства указывается единица измерений и нулевая точка. Примером может служить шенноновская мера информации. В этих шкалах помимо интервального свойства указывается единица измерений и нулевая точка.

Проблема выбора шкал имеет существенное значение для обоснования рациональных способов преобразования пространства описаний при решении задач классификации образов.