Алгоритм коррекции по ошибкам для двух классов

ПРОЦЕДУРА ОБУЧЕНИЯ ДЛЯ ДВУХ КЛАССОВ

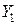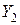При построении правила обучения для двух классов будем полагать, что существует множество векторов {w^*}, линейно отделяющих классы и , где 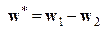. Это будет сделано с помощью алгоритма, известного под названием процедуры коррекции по ошибкам. Правило классификации совершенствуется с учетом лишь ошибок.

Алгоритм коррекции по ошибкам для двух классов

(1) Пусть w⁽ⁱ⁾ – приближение, используемое для классификации y⁽ⁱ⁾.

(2) w⁽¹⁾ = (0, …,0).

(3) При заданном векторе w⁽ⁱ⁾ действуют согласно следующим правилам.

Случай 1:(y)⁽ⁱ⁾ Î Y₁.

(а) Если y⁽ⁱ⁾ × w⁽ⁱ⁾ > 0, то w⁽ⁱ⁺¹⁾ = w⁽ⁱ⁾.

(b) Если y⁽ⁱ⁾ × w⁽ⁱ⁾ £ 0, то w⁽ⁱ⁺¹⁾ = w⁽ⁱ⁾ + y⁽ⁱ⁾

Случай 2: (y)⁽ⁱ⁾ Î Y₂.

(а) Если y⁽ⁱ⁾ × w⁽ⁱ⁾ < 0, то w⁽ⁱ⁺¹⁾ = w⁽ⁱ⁾.

(b) Если y⁽ⁱ⁾ × w⁽ⁱ⁾ ≥ 0, то w⁽ⁱ⁺¹⁾ = w⁽ⁱ⁾ – y⁽ⁱ⁾.

В более общем алгоритме w⁽¹⁾ – произвольный вектор, а коррекция по ошибкам заключается в добавлении ± cy⁽ⁱ⁾, где c – любая положительная постоянная, но это неоправданно усложнит изложение материала.

6.2. ЗАДАЧИ ГРУППИРОВАНИЯ В
РАСПОЗНАВАНИИ ОБРАЗОВ

Изначально устройство классификации должно решать, какие объекты следует группировать. Для установления принадлежности определенным классам некоторых объектов необходимо найти такое правило, которое позволило бы установить эту принадлежность. Задачи группирования встречаются во многих областях. В медицине разнообразные болезни, вызываемые различными микроорганизмами, часто группируются под общими названиями, например, «простудный катар» или «кишечное расстройство». В психиатрии классификация психических расстройств на «шизофрению», «маниакально-депрессивный психоз» и «психопатию» не так отчетлива, как хотелось бы. В биологии проблема группирования в семейства и роды обычно осуществляется на основе предположения об общности происхождения. По традиции о линиях эволюции судят по нескольким общим признакам, но в последнее время все чаще используются численные методы, подобные некоторым обсуждаемым нами далее.

В искусственном интеллекте задачи группирования изучались под названием «обучение без учителя». Хорошей иллюстрацией могут служить задачи шифрования и дешифровки информации,которые с помощью ЭВМ решаются намного проще, чем упомянутые выше задачи классификации болезней, хотя с формальной точки зрения они схожи.

Принципиальной основой алгоритмов решения данных задач является выбор процедуры группирования с точки зрения ее разумности (прямой метод), либо по заранее установленным критериям путем минимизации или максимизации некоторых функций оценки (непрямой метод). При выделении групп необходимо определять: они полностью независимые или связаны по определенной иерархии. Устанавливают также очередность выполнения процедуры прямого отнесения экспериментальных точек к отдельным группам и процессов вычисления функций при формировании данных.

Поскольку не представляется возможным охватить все множество методов, которые можно отнести к процедурам группирования, ограничимся рассмотрением наиболее используемых из них: метод непрямого группирования, прямого адаптивного группирования и иерархический прямой метод.