Статистическое группирование

По аналогии со статистической формулировкой задачи распознавания образов при статистическом группировании наблюдаемое множество данных X представляет собой n экспериментальных точек с неизвестной принадлежностью к классам. На первом этапе процесса наблюдения с каждым i-мклассом множества из k классов связывалась известная функция плотности вероятности f_i с неизвестными параметрами q_i. Например, если функция f_i является нормальным распределением, то множество параметров 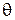содержит всего два параметра: среднее значение и дисперсию для класса i.На втором этапе выбор точки xдляi-го классаопределяется плотностью вероятностей f_i (x/q).

Задача группирования состоит в выборе значений для множеств
P = {p_i} и q = {q_i}, которые соответствуют данным множества X наилучшим образом. Поскольку с вычислительной точки зрения задача статистической оценки является достаточно сложной, дальнейшее рассмотрение будет ограничено широко используемым примером вычислений, известным как минимизация по критерию хи-квадрат.

Обозначим через 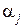число точек из множества X, попадающих в область 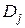пространства описаний D, состоящего из r попарно непересекающихся областей 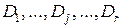. При любых фиксированных значениях P и q ожидаемое число наблюдений в области 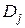с учетом попадания точек в нее из 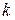областей различных классов равно

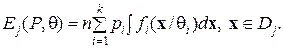(49)

Решение задачи состоит в определении значений P и q, которые минимизируют статистику хи-квадрат, равную

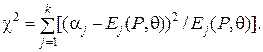(50)

В некоторых задачах надо найти и значение k. Конкретный способ решения зависит от вида функций плотности вероятностей {f_i}. Если не удается получить оценку в замкнутой форме, пробуют каким-то систематическим образом определить различные численные значения параметров. Когда исчерпывающее перечисление параметров также неосуществимо, может оказаться достаточно точной для практических целей процедура графической оценки, выполняемая с помощью ЭВМ.

6.2.2. Метод «k-средних»

Этот метод служит примером прямого адаптивного группирования для независимых классов. При его реализации, как и в задаче распознавания образов, экспериментальные точки упорядочены в последовательность S_x наблюдений x⁽¹⁾, …, x⁽ⁿ⁾ в m-мерном пространстве описаний. Предполагается, что число классов объектов ровно k, каждый класс имеет среднюю точку 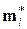, а текущее среднее значение корректируется по мере накопления новых данных.

Алгоритм, оценивающий 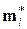по последовательности S_x, выглядит следующим образом:

1) Вычислить множество 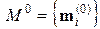начальных оценок, относя к каждому классу одну из первых k точек из последовательности S_x.
В результате получим

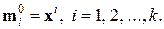
2) Отнести предъявляемую точку 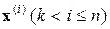к группе точек j, для которой расстояние 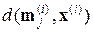минимально. Неопределенности нивелируются в пользу группы с меньшим индексом.

3) Найти новые оценки средних точек 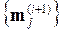для каждой группы:
если точка к группе j не отнесена, оценка 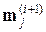оставляется без изменения; если отнесена к j, то на основе текущего состава группы устанавливается новая оценка средней точки. Пусть 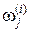– число экспериментальных точек в группе в момент, когда предъявляется i-я экспериментальная точка. Тогда

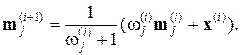
Математически доказано, что если последовательность S_x построена из выборок, относящихся к k различным распределениям вероятностей, то k оценок 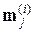будут асимптотически сходиться к средним значениям этих распределений.