Вероятностно-статистическое исследование

Спроса пассажиров на перевозки

Автомобилями-такси

Важное значение в организации таксомоторных перево­зок имеет определение закономерностей накапливания ав­томобилей-такси на стоянках. Процесс накапливания ав­томобилей-такси (приток) удобно представить числом их поступлений в интервале требований на поездки

Если в отдельные периоды времени среднее число при­бывающих автомобилей-такси в интервале спроса на них больше единицы — происходит их накапливание, а если в другие периоды времени — меньше, при этом очередь ожи­дающих прибытия пассажиров автомобилей-такси увеличи­вается Решение задачи определения целесообразного числа автомобилей-такси требует изучения распределения числа прибывающих автомобилей-такси.

Как показывают исследования, в большом числе случаев интервалы времени между очередным прибытием на стоян­ку автомобилей-такси подчиняются экспоненциальному рас­пределению с плотностью

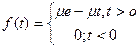(12.1)

где μ = 1/t — параметр распределения, t — средний интервал времени между очередными прибытиями на стоянку автомобилей такси

В этом случае число событий X, прибывающих автомо­билей-такси за время t, распределяется по закону Пуассона. Так как μ = 1/t — среднее число поступающих автомоби­лей-такси в единицу времени, то вероятность поступления X = т автомобилей-такси за время t

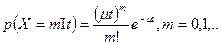
Пассажиры приходят на стоянку по одному и группами (групповые требования), поэтому поток требований на по­ездки не является простейшим. Исследования показывают, что гипотеза о пуассоновском характере прибытия пасса­жиров правдоподобна для ряда стоянок, т. е. можно полагать, что вероятность поступления на стоянку пассажиров за время t

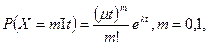
Интенсивности потоков автомобилей-такси μ и требова­ний на поездки Я в общем случае не совпадают. При μ > λ образуются устойчивые очереди автомобилей-такси.

Установим для условий простейшего пуассоновского по­тока прибытия автомобилей-такси и требований на поездки λ распределение случайной величины числа X — т поступающих автомобилей-такси в интервале требований на поездки. Полная вероятность события

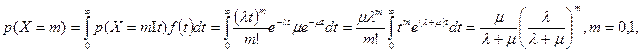
Это геометрическое распределение с параметром ρ = μ/(λ +μ). Для геометрического распределения вероят­ность поступлений т = 0,1... автомобилей-такси ρ_т — (1 - ρ) 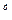ρ.

Несовпадение числа прибывающих автомобилей-такси и требований на них определяет функционирование стоянки как накапливающей системы. При достаточно высоком уровне удовлетворения требований на поездки в автомобиле-такси и хорошо организованных перевозках пассажиров другими видами транспорта (автобус, троллейбус, метро и др.) как правило, не образуется очереди пассажиров на сто­янках автомобилей-такси. В табл. 12.3 представлены дан­ные наблюдений числа прибытия автомобилей-такси на сто­янку в интервале между очередными требованиями на по­ездки.

В этом примере промежуток времени слишком мал для Наблюдений значительных изменений очереди, однако и здесь наглядно проявились характерные черты случайного характера образования очереди. При определенном избы­точном числе автомобилей-такси на стоянке часть вновь прибывших отправляется на другие стоянки без ожидания пассажиров. Для изучения закономерностей образования

Таблица 12.3

очереди автомобилей-такси необходимы массовые статисти­ческие наблюдения.

Процессы накапливания автомобилей-такси на стоянках оказывают определяющее влияние на организацию таксо­моторных перевозок.