Оптимизация управления процессом накапливания автомобилей-такси на стоянке

Степень удовлетворения спроса пассажиров на перевозки характеризуется коэффициентом, который определяется как отношение удовлетворенного спроса пассажиров на поездки к общему спросу.

Действительный спрос на перевозки может быть выявлен только в условиях полного удовлетворения требований на поездки. Косвенной характеристикой степени удовлетво­рения может служить относительная продолжительность времени, в течение которого спрос на перевозки удовлетво­ряется, т. е. Z_П 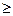1.

Эффективность таксомоторных перевозок зависит от боль­шого числа факторов, что затрудняет определение критерия оптимальности в общем виде. Кроме того, для возможно более полного удовлетворения спроса на поездки, дополни­тельно представляют интерес: доходы от перевозок за 1 ч ра­боты и на 1 км пробега; прибыль от перевозок за 1 ч ра­боты и на 1 км пробега; себестоимость 1 км платного про­бега; расход топлива на 1 км платного пробега (удельный расход топлива).

Одной из важных задач организации таксомоторных пе­ревозок является нахождение значения целесообразной длины очереди автомобилей-такси на стоянке по доходам и прибыли от перевозок и себестоимости 1 км платного про­бега.

Потери автотранспортного предприятия из-за простоев автомобилей-такси на стоянках на 1 ч работы

где Z — среднее число автомобилей-такси на стоянке; Z = 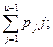С_н — накладные расходы на 1 ч работы автомобилей-такси.

Рассмотрим случай стационарного распределения по геометрическому закону числа поступающих на стоянку автомобилей-такси и в интервале времени между очередными требованиями на поездку При этом вероятность р_j = p^j+1 (1 — ρ /(1 — ρ 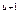), j= 1, 2, ..., u— 1, где и — предель­ная длина очереди автомобилей-такси. Потери в этом случае

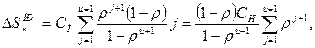
На рис. 12.8 представлена зависимость среднего числа автомобилей-такси в очереди и потерь на 1 ч работы (в руб­лях) от нормируемой предельной длины и очереди автомо­билей-такси. Как видно из рис. 12.8, эта зависимость близка к линейной.

Потери из-за отправки автомобиля-такси без пассажира, определяемые пробегом автомобиля-такси до очередной по­садки 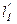(расстояние подачи) и затратами на 1 км пробега С_КМ составляют

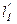С_КМ

гдеС_КМ ⁼ С_пер + С_н/ 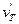, 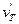— техническая скорость автомобиля такси при его подаче без пассажиров, км/ч.

Среднее число отправляемых без пассажиров автомоби­лей-такси в интервале времени между очередными требова­ниями на поездку

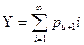
Как видно из рис. 12.9, с увеличением предельной дли­ны очереди автомобилей-такси потери ∆S 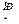, связанные с их простоем, возрастают, а потери, связанные с отправлением ∆S 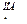автомобилей-так­си без пассажиров, снижают­ся. Зависимость суммарных

потерь 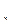(∆S 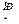= ∆S + ∆S 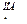) от предельного числа авто­мобилей-такси в очереди имеет явно выраженный экс­тремальный характер.

При организации таксомо­торных перевозок нельзя ру­ководствоваться только эко­номическими соображениями. Главным показателем каче­ства транспортного обслуживания пассажиров является степень удовлетворения требова­ний пассажиров на поездки. Поэтому представляет практи­ческий интерес определение длительности периода, в те­чение которого на стоянке гарантируется наличие автомо­билей-такси.

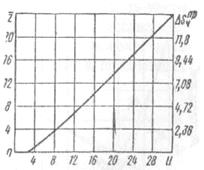
Рис. 12.8. Среднее число ав­томобилей-такси в очереди и потери от простоя на 1 ч в за­висимости от предельной дли­ны очереди И

Рассматривая функционирование стоянки автомобилей-такси как накапливающей системы, среднюю длительность периода наличия автомобилей-такси на стоянке (ненулевой уровень), измеряемую числом интервалов N_n времени между поступлением очередных требований на поездки, для гео­метрического распределения числа поступающих требова­ний в этом интервале можно определить по формуле

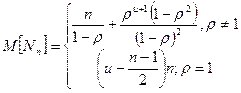(12.3)

где п — число автомобилей-такси в очереди

Как видно из формулы (12.3), средняя длительность не­нулевого уровня при заданном притоке ρ 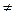1 и предельной длине очереди U находится в линейной зависимости от числа п автомобилей-такси в очереди.

Средняя длительность периода (математическое ожида­ние) ненулевого уровня, измеряемая в минутах,

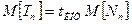
Из рис. 12.10 видно, что при наличии в очереди п — 10 автомобилей-такси (при предельном и = 15) математическое ожидание длительности перио­да ненулевого уровня М [N_n] при ρ, равном 0,8, составляет 50. Это значит, что в среднем будет удовлетворено 50 требо­ваний на поездки до наступ­ления момента, при котором на стоянке автомобили-такси будут отсутствовать.

При из­вестной средней длительности интервалов времени между очередными требованиями на поездки легко определить и длительность периода наличия автомобилей-такси на стоянке в минутах (часах)

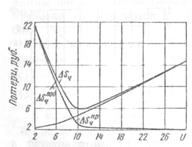
Рис. 12.9. Потери от простоя автомобилей-такси и подачи их без пассажиров в зависимости от и

При ρ 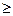1 очередь автомоби­лей-такси возрастает, и удовлетво­рение требований на поездки га­рантируется при любом достаточ­но большом числе п автомобилей-такси в очереди.

Рис 12.10. Зависимость средней длительности периода наличия автомобилеи-такси на стоянке от их числа в очереди (u=15)

Исследование длительности ма­тематического ожидания периода наличия автомобилей-такси на стоянке с учетом изменения сред­него числа поступающих автомоби­лей-такси ρ в интервале времени на поездки t_ИНТ в отдельные периоды позволяет правильно назна­чать целесообразное число U автомобилеи-такси на стоянке, руководствуясь соображениями возможно полного удовлетворения и спро­са на поездки.

Самостоятельного решения требует вопрос определения рациональной длины очереди автомобилей-такси на уда­ленной стоянке с большим пассажирообменом.

Рассмотрим решение задачи на примере транспортного обслуживания аэропорта. Аналогичная задача возникает при обслуживании железнодорожных станций, речных и морских портов и других мест, где организация транспорт­ного обслуживания контролируется диспетчером.

Чтобы установить предельно допустимую длину оче­реди автомобилей-такси в аэропорте, определим сопостави­мые доходы и прибыль в случае, когда автомобиль-такси ожидает в очереди и когда он уезжает без пассажиров. В первом случае время цикла перевозок, включающего ожидание посадки, движение с пассажирами и оплаченный простой (подача отсутствует),

,

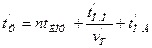где tо.п — средний оплаченный пробег за цикл перевозок, км; 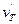— техническая скорость автомобиля-такси при доставке пасса­жиров к месту назначения в городе, км/ч; t 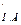—время оплаченно­го простоя, приходящееся на один цикл перевозок, ч

Доходы перевозок по действующим тарифам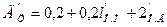

Для сопоставимости далее будем определять доходы, рас­ходы и прибыль при убытии автомобиля-такси без пассажи­ров в расчете на время цикла перевозок.

При убытии автомобиля-такси без пассажира доходы за то же время цикла t'_ц перевозок:

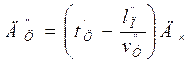, (12.4)

где Д_ц — доходы за 1 ч работы автомобиля-такси в городе, р

Предельно допустимую длину очереди в аэропорте по доходам на перевозки определяем из условия 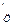Д = Д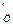

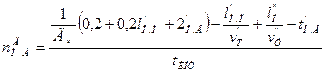, (12.5)

Прибыль при простое автомобиля-такси в очереди за время цикла перевозок 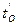с учетом 2 % отчислений на строи­тельство и эксплуатацию автомобильных дорог

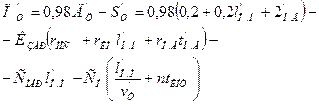(12.6)

где 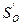— расходы за цикл перевозок.

Преобразовав выражение (12.6), получим

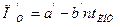(12.7)

где

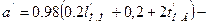
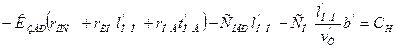
Как видно из уравнения (12.7), размер прибыли от пе­ревозок за время цикла 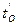находится в линейной зависимости от числа п автомобилей-такси в очереди и интервала време­ни tинт между очередными требованиями на поездку.

При убытии автомобиля-такси из аэропорта без пасса­жира прибыль за время цикла перевозок

,

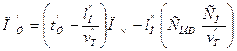Подставив в эту формулу значение 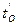, после преобразо­ваний получим:

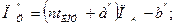
где

.

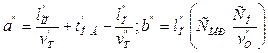Предельно допустимая длина очереди в аэропорте по прибыли от перевозок, определяемая из условия П 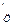= П ,

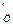(12.8)

Таким образом, для определения предельно допустимой длины очереди в аэропорте необходимо знать средние ин­тервалы времени между очередными требованиями на по­ездки и прибыль или доходы в зависимости от выбранно­го критерия оптимизации на 1 ч работы автомобиля-такси в городе.

Как показали исследования, спрос на перевозки в аэро­порте и городе, доходы и прибыль на 1 ч работы в городе ме­няются по часам суток, как и средние интервалы прибытия пассажиров на стоянку автомобилей-такси в аэропорты (рис. 12.11).

По формулам (12.5) и (12.8) могут быть построены номограммы для определения рационального числа автомобилей-такси в очереди на стоянке. Такие номограммы Для решения задачи по кри­терию максимальных прибы­ли и доходов представлены на рис. 12.12. Пользуясь ими, легко устанавливаем предельно допустимое число автомобилей-такси на стоян­ке в аэропорте.

Рассмотрим конкретный пример. В рассматриваемом промежутке времени доход за 1 ч работы автомобиля-такси в городе составляет 4,25 р., прибыль— 1,3 р. Средний ин­тервал прибытия пассажиров на стоянку 2,71 мин. Пользу­ясь номограммами (рис. 12.12), устанавливаем рациональное число автомобилей-такси на стоянке.

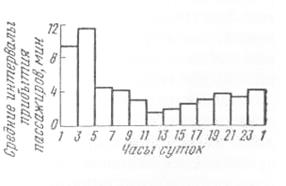
Рис. 12.11. Распределение ин­тервалов, убытия автомобилей-такси по часам суток

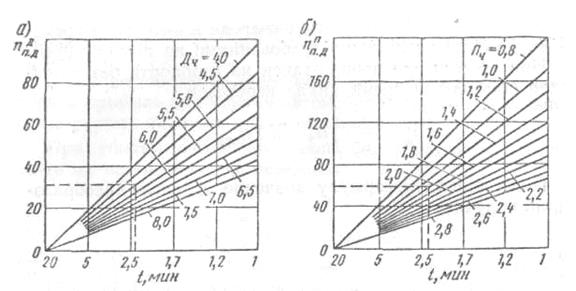
Рис. 12.12. Номограммы для определения предельно допустимого числа автомобилей-такси в очереди на стоянке аэропорта в зависи­мости от интервала прибытия пассажиров t_ИНТпо критерию макси­мума доходов (а) и прибыли (б)

Для определения рационального числа автомобилей-такси в очереди используют таблицы. Исходными данными для построения таблиц, как и номограмм, являются распределение доходов и прибыли по часам суток и средние интервалы времени прибытия пассажиров на стоянку.