Иерархическое группирование. При иерархическом группировании данные, подлежащие группированию, берутся из единственного класса, который можно разбить на подклассы и подклассы подклассов

При иерархическом группировании данные, подлежащие группированию, берутся из единственного класса, который можно разбить на подклассы и подклассы подклассов. Этот метод можно использовать в евклидовом и в неевклидовом пространстве, если меру расстояния между двумя точками определить в качестве меры расстояния между любыми двумя точками множества X. Этапами реализации метода иерархического группирования являются:

1) Пусть элементами матрицы H служат расстояния между парами экспериментальных точек:

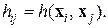
2) В процессе группирования каждую экспериментальную точку будем относить к классу, содержащему только ее саму 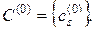Ясно, что расстояние между любыми двумя «скоплениям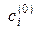и» и 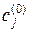в этом случае равно

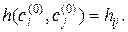(51)

3) Если проведено группирование 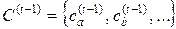, определена соответствующая матрица Hс элементами 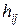, как в (51), а 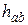– наименьший элемент матрицы H ( 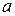и 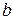– индексы двух ближайших скоплений), тогда группирование 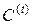получается из группирования 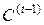объединением элементов a и 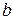в одну группу .

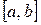4) Переопределим матрицу H, используя правило максимума

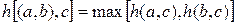(52)

или правило минимума

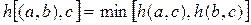. (53)

При получении в (52) результата 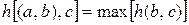, из матрицы H вычеркиваются все расстояния, связанные с элементом a. Если 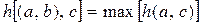, из матрицы H удаляются все расстояния, связанные с элементом b. При использовании критерия (5310) из матрицы H удаляются все расстояния, связанные с элементами a или b, при
получении соответственно результата 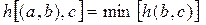или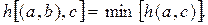

5) Повторяем шаги 3 и 4 до тех пор, пока все начальные экспериментальные точки не объединятся в одну группу.

Формируемые этим алгоритмом классы можно интерпретировать графически следующим образом. Для данного скопления точек определяется его диаметр как наибольшее расстояние между любыми двумя его точками. При использовании правила максимума (52) на каждом этапе формируются группы наименьшего диаметра. Для иллюстрации эффекта применения правила минимума (53) рассмотрим цепь от точки x до точки y, т. е. такую последовательность экспериментальных точек 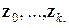что 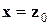, 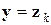. Правило (53) минимизирует на каждом этапе длину цепи между любыми двумя точками группы. Таким образом, правило максимума приводит к такой иерархии групп, при которой минимизируются диаметры, а правило минимума – к такой иерархии, при которой минимизируется расстояние между соседними точками цепи в пределах одной группы.

Приведем пример применения рассмотренной процедуры иерархического группирования для решения задачи акустической неразборчивости. В эксперименте испытуемых просили идентифицировать фонемы в плохих условиях слышимости. Полученные результаты оформлялись в виде «матрицы неразборчивости», элементами которой являлись вероятности распознавания фонема i, в то время как была произнесена фонема j. Определены следующие группы для одного уровня различимости: глухие взрывные 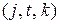, звонкие взрывные 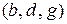, глухие фрикативные 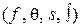, звонкие фрикативные 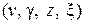, «носовые» 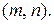Таким образом, этот алгоритм произвел деление на группы, имеющие близкий акустический смысл. Аналогичного рода результаты получены в ряде приложений теории поведения.