Аналитическое представление конфигурации расчетной схемы сети

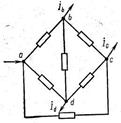
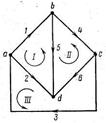
На рис. 2 показан пример расчетной схемы многоконтурной сети. Взаимная связь шести ветвей и четырех узлов этой схемы показана отдельно на рис. 3. Если каждой ветви схемы поставить в соответствие некоторое произвольно выбранное направление, то будет получена схема, которая называется направленным графом.

Рис. 2	Рис. 3

Направленный граф харак­теризует конфигурацию — геометрический образ схемы. Для его аналитического представления необходимо провести ну­мерацию ветвей и независимых контуров и выбрать направ­ление обходов этих контуров, принимаемое за положительное. Направленный граф схемы может быть описан с помощью двух матриц, называющихся 1 и 2-й матрицами соединений, или инциденций. Первая матрица соединений М, называе­мая иногда матрицей соединений в узлах, представляет собой таблицу, каждая строка которой отвечает одному из узлов схемы, за исключением балансирующего, а каждый столбец — одной из ее ветвей. В клетках этой таблицы проставляется «0», если ветвь не связана с узлом, которому соответствует строка. Если же ветвь связана с узлом, то в клетке простав­ляется либо «+1», либо «—1», в зависимости от направления ветви в направленном графе схемы. Если данный узел является началом ветви, и ветвь выходит из рассматриваемого узла, то в матрице соединений (инциденций) ставится «+1». Если же ветвь входит в узел, который в этом случае считает­ся концом ветви, то в соответствующей клетке первой матри­цы соединений проставляется «—1».

Применительно к направленному графу, показанному на рис. 5-3, первая матрица соединений, составленная по сфор­мулированному правилу при балансирующем узле а, имеет вид

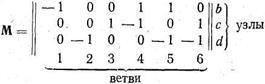
Вторая матрица соединений (инциденций) N, называемая также матрицей соединений в контурах, представляет собой таблицу, строки которой отвечают независимым контурам направленного графа схемы, а столбцы — его ветвям. Если та или иная ветвь входит в контур, то на пересечении соответ­ствующих строки и столбца матрицы N ставится либо «+1», либо «—1» в зависимости от того, совпадает направление ветви с направлением обхода контура, или имеет противопо­ложное ему направление. Если же ветвь не входит в контур, то в матрице N на пересечении строки и столбца, отвечающих рассматриваемым контуру и ветви, записывается «0». Это правило образования второй матрицы соединений позволяет для направленного графа схемы, изображенной на рис. 3, получить

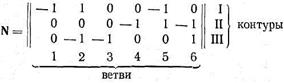
В схеме сети и ее направленном графе удобно выделить две группы ветвей. Первая из них образует так называемое дерево сети (графа), а вторая — ее хорды. К дереву относится наименьшая часть замкнутой схемы, ветви которой соединяют балансирующий узел со всеми другими узлами. В сложной схеме могут быть выделены несколько деревьев. На рис. 4, а, б, в показаны примеры деревьев, отвечающих схеме сети, приведенной на рис. 3. Причем ветви, входящие в дерево, отмечены сплошными линиями, а ветви, являющиеся хорда­ми,— штриховыми. Для всех деревьев схемы характерно ра­венство числа ветвей (1…4)числу узлов (b...d),без балансирующего узла, поэтому первая матрица соединений (инциденций) для дерева схемы М имеет квадратную форму.

При нумерации ветвей направленного графа целесообраз­но ветвям, входящим в дерево, присваивать последовательные номера, начиная с первого. Если в рассматриваемом примере направленного графа (см. рис. 3) в дерево включить ветви 1, 2 и 3 (рис. 4, а), то в первой матрице соединений первые три столбца будут отвечать дереву схемы, а последующие — ее хордам.

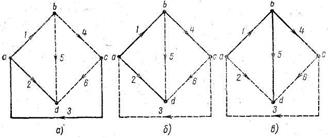
Рис. 4.

Нетрудно видеть, что в этом случае матрица М может быть разбита на две подматрицы М_a и М_b

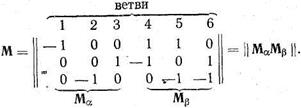
В сложной матрице М при таком подходе подматрица М_a ха­рактеризует связь ветвей дерева схемы с ее узлами, а подмат­рица М_b —взаимную связь между хордами и узлами схемы.

Уравнения законов кирхгофа и ома в матричной форме

Найдем произведение первой матрицы соединений (для направленного графа первой лекции), на столбцевую матрицу токов в ветвях этой схемы:

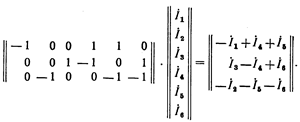
Примем, что токи в ветвях имеют направление, совпадающее с направлением соответствующих ветвей в направленном графе (рис. 5). Тогда в соответствии с 1 законом Кирхгофа будем иметь:

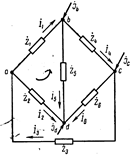Рис. 5.

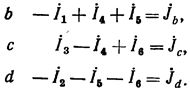
Алгебраические суммы в левых частях записанных уравнений образуют матрицу, полученную при умножении матриц М и I. Следовательно,

Это матричное уравнение в обобщенной форме определяет I закон Кирхгофа.

Запишем совокупность падений напряжения в сопротивлениях ветвей рассматриваемой схемы в форме столбцевой матрицы

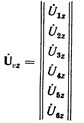
и найдем произведение второй матрицы соединений N на матрицу .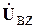

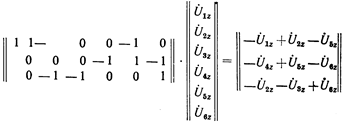
В результате перемножения получена матрица, каждая строка которой определяет сумму падений напряжения в сопротивлениях ветвей в одном из независимых контуров. В рассмотренном частном примере каждая из этих сумм равна нулю. В общем случае, при наличии э.д.с. в ветвях схемы, сумма падений напряжения в сопротивлениях ветвей, составляющих независимые контуры, в соответствии со II законом Кирхгофа должна быть равна сумме э.д.с., входящих в соответствующий контур. Если совокупность таких сумм, каждая из которых определяет э.д.с. называемую контурной, записать в форме столбцевой матрицы, то II закон Кирхгофа получит выражение

Предположим, что источники э.д.с. включены в каждую из ветвей схемы и их совокупность образует столбцовую матрицу 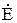. В этом случая матрица 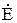полностью подобна матрице 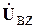. Поэтому произведение матрицы N на матрицу 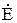определит матрицу, в каждой строке которой будет сумма э.д.с., входящих в один независимый контур, аналогично тому, как произведение матриц N и 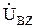определило матрицу суммы падений напряжения в ветвях этих контуров. Следовательно,

а уравнение (5-2) может быть также записано в виде

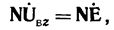
или

Падения напряжения в сопротивлениях ветвей зависят от токов и сопротивлений этих ветвей. Аналитически имеющаяся здесь зависимость может быть записана в матричной форме с помощью матрицы сопротивлений ветвей. Эта матрица имеет квадратную форму, ее строки и столбцы отвечают ветвям рассматриваемой схемы. Сопротивления ветвей располагаются по главной диагонали этой матрицы. Если же в схеме имеются ветви, связанные магнитным потоком взаимной индукции, то матрица сопротивлений ветвей должна содержать сопротивления взаимоиндукции на пересечении строк и столбцов, отвечающих магнитносвязанным ветвям. Матрица сопротивлений ветвей, составленная по такому принципу применительно к схеме рис. 1, имеет вид

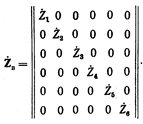
Произведение матрицы сопротивлений в ветвях на матрицу токов ветвей позволяет получить матрицу падений напряжения в сопротивлениях ветвей.

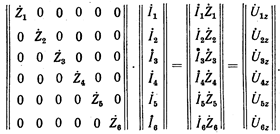
Следовательно, в обобщенной форме можно записать

Из (5-4) и (5-5) имеем

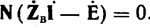
Обозначим

где U_B—матрица падений напряжения в ветвях, в общем случае содержащих э.д.с. Выражение (5-6) является матричной формой записи закона Ома

.