Графическое и аналитическое представление характеристик крупности
Результаты ситового анализа представляют в виде таблиц или графиков.
Гранулометрической характеристикой называют табличное или графи-ческое отображение гранулометрического состава полезного ископаемого.
На обогатительных фабриках для контроля гранулометрического состава в процессах дробления, измельчения и грохочения применяют ситовый анализ.
Характеристики крупности строят в прямоугольной системе координат следующим образом: частные – по выходам отдельных классов; суммарные (кумулятивные, накопительные) – по суммарным выходам классов на диаметре каждого из сит.
На оси ординат откладывают в масштабе частный или суммарный выход классов (в процентах), на оси абсцисс — в масштабе размеры отверстий сит в миллиметрах. Возможно построение ординат, определяющих выхода отдельных классов, на большем или меньшем из диаметров, ограничивающих класс крупности, а также на диаметре куска, среднеарифметическом для двух крайних диаметров.
По выходам отдельных классов можно также строить графики, называемые столбиковой диаграммой. Она составляется из прямоугольников, высота которых пропорциональна выходам отдельных классов, а основанием служит интервал крупности классов.
Если по оси ординат отложены суммарные выходы материала крупнее диаметра отверстий данного сита, то суммарная характеристика построена «по плюсу», если мельче данного диаметра, то – «по минусу». Обе характеристики зеркально отражают одна другую и пересекаются в точке 50% - ного выхода.
При этом выход какого-либо класса (- d 1 + d 2) определяется по суммарной характеристике разностью ординат, построенных на диаметрах d 1и d 2 .
Изменение шкалы сит изменяет вид частной характеристики, поэтому по ее виду нельзя судить о распределении крупных и мелких зерен. Суммарная характеристика крупности позволяет определить выход любого класса.
Данные ситового анализа графически представляют в виде следующих характеристик:
- частные – по выходам отдельных классов;
- суммарные - «по плюсу» и «по минусу»;
- полулогарифмические;
- логарифмические;
- характеристики крупности по Розину –Раммлеру;
- дифференциальные функции распределения по крупности.
В системе координат с полулогарифмическими (1) или логарифмическими (2) шкалами графики строят следующим образом:
1 - по оси абсцисс откладывают логарифмы размеров сит;
2 - по оси ординат откладывают также логарифмы суммарных выходов классов.
Преимущество полулогарифмического масштаба по сравнению с линейным состоит в том, что расстояния между соседними значениями размеров сит на оси абсцисс в области мелких зерен увеличиваются, а в области крупных — сокращаются. Это позволяет правильно отсчитывать выхода мелких классов.
Построение полулогарифмических характеристик упрощается, если набор сит имеет постоянный модуль, так как отрезки на оси абсцисс будут одинаковой величины. Например, для модуля М шкалы грохочения (классификации) определим разницу между логарифмами размеров отверстий смежных сит:
| Размеры отверстий сит l | Логарифмы размеров отве-рстий сит | Разность между логариф-мами размеров отверстий сит |
| l1 | lgl1 | - |
| l1M | lgl1 + lgM | (lgl1+ lgM) – lgl1= lgM |
| l1M2 | lgl1+ 2 lgM | (lgl1+ 2lgM)- (lgl1 + lgM)= =lgM |
Каждый отрезок на оси абсцисс между соседними ситами равен lg M. При построении характеристики за lg Mможно принять произвольный отрезок.
Следует иметь в виду, что выходу 0% соответствует по оси абсцисс lg 0 = - ¥. Поэтому левая ветвь полулогарифмической кривойне доходит до ординаты на уровне 0 %.
Построение гранулометрических характеристик в логарифмических коорди-натах нередко используют для изучения закономерностей распределения материалов по крупности. Логарифмическая характеристика крупности по минусу для дробленых и измельченных пород часто получается прямолинейной.
Дифференциальные функции распределения g(х) по крупности показывают число зерен или массовые выходы классов крупности.
Число зерен в каждом классе или их массу называют численностью, частотой или частостью класса. При этом ординаты функции распределения выражают частость на единицу длины узкого интервала по оси абсцисс – 1/мкм (см. источник 2, рис. 11: 2.Перов, Андреев, Биленко, 1990 г., стр. 30).
Примечание.
Для построения функции распределения по числу зерен следует:
1)по оси абсцисс на интервале (xn - xn –1 ) построить прямоугольник высотой Nn /N. D xn или Wn /W. D xn ,
где: D xn = xn - xn –1 - число зерен в этом классе;
Wn - масса зерен в этом классе;
Nn /N - частость по числе зерен;
Wn /W - частость по массе зерен;
W - общая масса зерен;
N - общее число зерен.
2) Соединить кривой точки на серединах верхних сторон прямоугольников.
Пример суммарной характеристики крупности, построенной по данным табл. 3.1. показан на рис. 3.3.
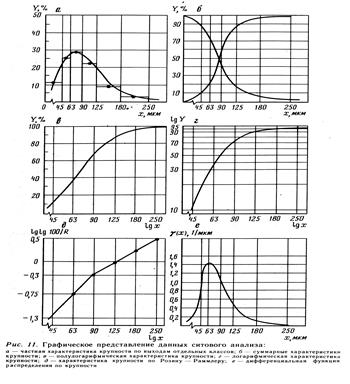 |
Рис. 3.3 Дифференциальная функция распределения g (х)
Таблица.3.1.
Результаты ситового анализа
| Диаметр сита, мм | Классы крупности, мм | Частный выход | Суммарный выход | ||
| кг | % | по "+" | по "-" | ||
| + 25 | |||||
| -25+13 | 4,5 | ||||
| -13+6 | 6,0 | ||||
| -6+3 | 9,0 | ||||
| -3+1 | 4,5 | ||||
| -1+0 | 6,0 | ||||
| Итого | 30,0 | 100,0 |
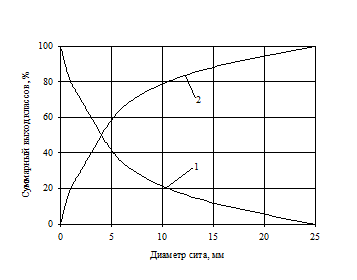
Рис. 3.3. Суммарные характеристики крупности: 1-по "плюсу"; 2-по "минусу .
Задача 6. По данным таблицы построить гранулометрические характеристики продуктов 1, 2 и 3 (суммарные по плюсу и минусу); определить и на графиках обозначить суммарный выход класса минус 5 мм и плюс 10 мм.
Результаты ситового анализа. Таблица
| Класс Диам. | Продукт 1 | Продукт 1 | Продукт 2 | Продукт 2 | Продукт 3 | Продукт 3 |
| мм сита, мм | Выход, % | Выход, % | Выход, % | Выход, % | Выход, % | Выход, % |
| Частн. | Суммарн. по (+) по (-) | Частн. | Сумм. по плюсу | Частн. | Сум. по плюсу | |
| +30 30 | 0 100 | |||||
| -30+20 20 | 53 47 | |||||
| -20+10 10 | 82 18 | |||||
| -10+5 5 | 91 9 | |||||
| -5+2,5 2,5 | 96 4 | |||||
| -2,5+1,3 1,3 | 98 2 | |||||
| -1,3+0 | 100 0 | |||||
| Итого | - | - | - |
По кривой суммарной характеристики можно определить теоретический выход любого класса крупности при грохочении материала по заданному размеру. Например, при грохочении продуктов 1-3 (см. задачу 6) на ситах с размером отверстия 15 мм теоретический выход надрешетного продукта составит: для продуктов 1 - 70%, 2 - 27% и 3 - 8% (см. рис. ниже).
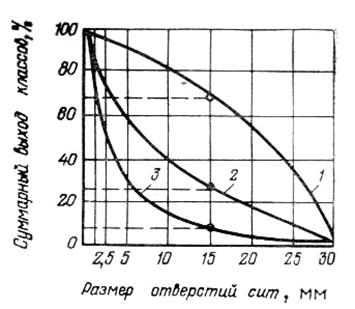 |
Рис. Гранулометрические характеристики продуктов 1, 2, 3 (см. задачу 6)
По виду кривой можно судить о преобладании крупных или мелких классов в исследуемом продукте: выпуклая кривая продукта 1 свидетельствует о том, что в этом продукте больше крупных частиц, чем в продуктах, характеризующихся вогнутыми кривыми, характеризующими продукты 2 и 3.
Задача 7.
По результатам ситового анализа угля (см. табл.) определить зольность класса +100 мм и общую зольность угля.
Результаты ситового анализа угля. Таблица
| Класс, мм | Продукт | g, % | Ас, % |
| + 100 | уголь | 1,6 | 8,7 |
| +100 | сростки | 1,4 | 38,5 |
| +100 | порода | 3,6 | 79,5 |
| +100 | Итого | 6,6 | ? |
| +50-100 | уголь необогащен. | 7,0 | 24,4 |
| +25-50 | то же | 9,2 | 26,7 |
| +13-25 | то же | 9,9 | 20,4 |
| +6-13 | то же | 14,4 | 20,9 |
| +3-6 | то же | 6,4 | 19,3 |
| +1-3 | то же | 19,0 | 21,3 |
| +0,5-1 | то же | 11,5 | 22,4 |
| +0-0,5 | пыль | 16,0 | 22,0 |
| Всего | ? |
Построение гранулометрических характеристик в логарифмических координатах используют для изучения закономерностей распределения материалов по крупности. Для этой цели суммарные характеристики крупности описывают аналитически уравнениями одного вида. Наиболее часто для этих целей используют уравнение Розина — Раммлера:
R = 100 ехр (- bd n ),
где R — суммарный выход класса крупнее d (остаток на сите), %; d — размер отверстий сита; b, n — параметры, зависящие от свойств материала.
Если взять логарифмическую характеристику материала "по минусу", то его гранулометрический состав можно представить уравнением
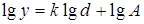 ,
,
где y - cуммарный выход класса мельче отверстий сита (по минусу);
k - коэффициент, равный тангенсу угла наклона прямой;
d - размер отверстий сита;
lg A - отрезок, отсекаемый прямой на оси ординат.
Переходя к антилогарифмам, получим:
y = Ad k.
Данное уравнение суммарной характеристики называют уравнением "Годэна-Андреева". Значение показателя k определяет направление и степень изгиба гранулометрической характеристики.
Если характеристику построить "по плюсу", то она будет: при k>1 - выпуклой, при k<1 - вогнутой и при k=1 - прямой. Следовательно, по значению k можно судить о преобладании в материале крупных или мелких зерен.
Лучшее согласие с экспериментальными данными дает уравнение Розина -Раммлера,выведенное на основе большого количества данных гранулометри-ческого анализа сыпучих материалов:
R = 100 ехр (- bd n ) , 100/R = е bd n ,
где R — суммарный выход класса крупнее d (остаток на сите), %;
d — размер отверстий сита;
b, n — параметры, зависящие от свойств материала и размерности d (мм, см, мкм); n – тангенс угла наклона прямой к оси абсцисс.
Из практики установлено, что чем > зерен менее 1 мкм, тем > b.
Величина n характеризует степень вогнутости кривой суммарных остатков
R= f (d / dс),
где dс – размер отверстий сита, на котором получают стандартный остаток
Rс= 36,8 %.
Произведем двойное логарифмирование данного уравнения 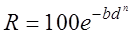 или 100/R = е bd n
или 100/R = е bd n
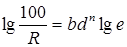
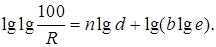
|
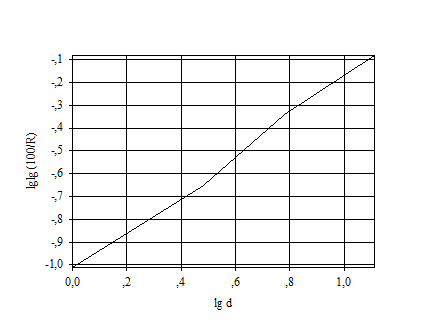
| Рис. 3.4. Характеристика крупности по Розину-Раммлеру |
Уравнение Розина-Раммле-ра в координатах 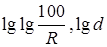 изображается прямой линией с угловым коэффициентом n (см. рис. 3.4).
изображается прямой линией с угловым коэффициентом n (см. рис. 3.4).
Параметры b и n нахо-дят по двум известным точкам, удаленным макси-мально одна от другой; для них определяют значе-ния 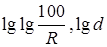 , решая уравнения:
, решая уравнения:
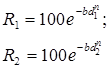 .
.
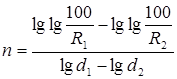 .
.
Знаяn, можно определитьb: 100/R1= е bd1 n
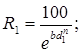

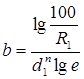
Дата добавления: 2016-01-26; просмотров: 9894;
