Математическая модель системы ТРО

Наиболее экономный метод решения проблемы – математическое моделирование.

Исходная информация:

ü решения L={l₁,…,l_k}; L=(g₁,…,g_n)

ü априорный словарь 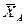={x₁,…,x_n}

ü объекты Q={w₁,…,w_z};

ü ресурсы С₀;

ü выигрыши .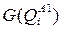

Последовательность построения модели:

Первый этап: 1) построение модели в первом приближении (итеративная процедура), т.е. a=1;

- определяется первый вариант разбиения множества объектов

на классы А₁, в соответствии с чем их количество m1=k+1;

- при этом к классу Q₁^A1 относятся объекты, применительно к

которым следует принимать решение L₁, к классу Q₂^A1 – решения L₂ и т.д., к классу 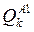- решение L_k, к классу 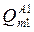- решение не принимается;

2) непосредственно определяется подмножество объектов каждого класса:

;

,

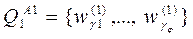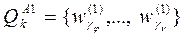где {(g₁,..,g_j},…,(g_j,…,g_n)}Î1,…,z; разрабатывается набор правил относительно значений признаков, содержащихся в априорном словаре, в соответствии с которыми на основе методов самообучения (при известном числе классов) определяются объекты исходного множества, относящиеся к каждому классу.

3) производится описание каждого класса на языке признаков априорного словаря и находятся наилучшие решающие границы между классами;

4) на очередном шаге проверяется достаточность С₀: если 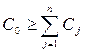, то можно использовать все признаки априорного словаря, с при С₀< 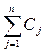при обеспечении минимума среднего риска или максимума среднеквадратического расстояния между классами или экстремума другого критерия, формируется соответствующее подмножество признаков;

5) производится описание классов Q^A1_i, i=1,…,m на языке рабочего словаря первого приближения и определяются наилучшие границы между ними.

6) делается очередной шаг, на котором оценивается величина вероятности правильного решения задачи распознавания

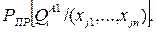-предмет построения соответствующей локальной модели

7) вычисляется первое приближение величины R⁽¹⁾.

Второй этап: 1) уточняется модель системы в смысле max R

,

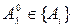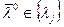
В алфавите классов первого приближения определяется такой класс 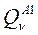, для которого величина 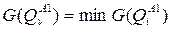. Это означает, что к классу Q_n относятся объекты, распознавание которых обеспечивает (по сравнению с распознаванием объектов других классов) наименьший выигрыш.

2) из алфавита классов первого приближения исключается класс 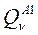, а объекты того класса надлежит отнести к такому классу 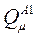, для которого уменьшение величины 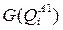, i=1,…,m минимально, т.е. .

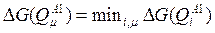Таким образом, определяется второй вариант разбиения объектов на классы А₂, применительно к которому вновь применяют операции 1)¸7) и определяется второе приближение – R⁽²⁾.

Через несколько итераций достигается такое построение систем, при котором R достигает максимума.