Управление процессом распознавания
По мере накопления апостериорной информации о признаках точность распознавания объектов увеличивается.
Пусть задан алфавит классов Q={Q1,…,Qm}, признаки XA={x1,…,xn}, а также функции плотности fi(xj), i=1,…,m, j=1,…,n.
Вероятность получить однозначное решение по одному признаку Xj, j=1,…,n, равно вероятности попадания соответствующей случайной величины в такие интервалы D1, ..где отлична от нуля одна из функций fi(xj), i= 1,…,m. Обозначим это событие через P(an). Пусть P(an) 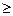 e>0 при любом g. Тогда
e>0 при любом g. Тогда 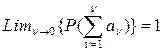 , n - число признаков, используемых при распознавании.
, n - число признаков, используемых при распознавании.
Следствие: Таким образом, если n возрастает, то увеличивается и вероятность однозначного решения задачи распознавания, которая при n®¥ стремится к единице.
Поскольку накопление информации сопряжено с затратами, то возникает и задача оптимального управления процессом распознавания.
Пусть известны априорные вероятности появления объектов соответствующих классов P(Qi), i = 1,…,m, а также – затраты за попытки переклассификации и плата за принятие окончательных решений.
Качество каждого алгоритма, определяющего последовательное правило R, охарактеризуем функционалом, представляющим собой математическое отклонение от величины средних расходов ИР:
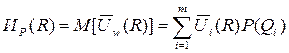
Задача состоит в том, чтобы найти такое 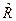 , которое обеспечивает минимум функционала UP(R), причем
, которое обеспечивает минимум функционала UP(R), причем 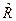 должно быть согласовано с системой ограничений.
должно быть согласовано с системой ограничений.
Следствие 2: В любом случае продолжение или окончание итеративного процесса управления должно оцениваться:
- риском прекращения экспериментов;
- риском их продолжения после окончательного числа шагов.
В основе того лежит оптимальное байесово последовательное правило. При планировании процесса распознавания количество стадий экспериментирования можно ограничить некоторым числом N. Порядок управления экспериментами (до тех пор, пока их выгодно продолжать) определяется с помощью функции риска 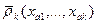 .
.
Дата добавления: 2016-01-20; просмотров: 830;
