Общая постановка проблемы распознавания

Проблема распознавания, прежде всего, состоит в том, чтобы определить словарь признаков и алфавит классов.

Эффективность действий системы управления (надсистемы) определяется достоверностью решения задачи распознавания, которая зависит от количества апостериорной информации о распознаваемом объекте, т.е. размера словаря признаков (при условии, что объем априорной информации обеспечивает построение надежных описаний классов на языке признаков).

Следствие 1: Расширение словаря признаков неизбежно сопряжено с увеличением затрат ресурсов материальных, габаритных, энергетических и т.п., т.е. на величину ресурсов налагаются определенные ограничения. При этом алфавит классов целесообразно расширять до m + 1, где m – число управляющих решений. Однако при заданном словаре признаков увеличение числа классов уменьшает вероятность правильного распознавания, т.е. необходим компромисс между размерами алфавита классов и объемом рабочего словаря. Какая же цена этого компромисса в плане оптимальности решения?

Следствие 2: При сильно коррелированных признаках увеличение временных и аппаратных затрат не приводит к увеличению признакового пространства (расширению словаря). Такие параметры -малоинформативны.

Рассмотрим формальную постановку задачи:

1. Пусть задано множество объектов Q = {Q_i}, i=1,…,m и множество

управлений (стратегий) L = {L_j}, j=1,…,k.

2. Введем в рассмотрение множество возможных вариантов разбиения

объектов на классы А = {a_a}, a = 1,…r.

3. Будем полагать, что если выбран вариант разбиения А_a, a = 1,…r, то Q

подразделяется на m₂ классов, т.е.

A_a: Q^Aa_qÇQ^Aa_g=Æ

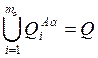q, g = 1,…,m_a, q¹g.

4. Пусть первоначальная информация позволяет построить априорное

признаковое пространство (априорный словарь признаков), описываемое многомерным вектором: .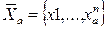

5. Информация относительно множества решений L = {l₁,l₂,…,l_k}

позволяет произвести разбиение множества объектов на классы – составить априорный алфавит классов.

Пример 1: Вариант 1: a=1, т.е. А_a=А₁, тогда число А₁ равно m_a=m₁=k+1.

6. Исходное множество объектов Q = {Q₁,…,Q_m} расценим как

обучающую выборку и подразделим на подмножества – классы:

Q^A1_1; Q^A1₂,…, Q^A1_m1=k+1.

При том: если обучающая выборка достаточно представительная, то путем обработки исходной информации можно определить описание классов.

Пример 2: В случае статистического подхода к задаче распознавания такими описаниями являются:

ü априорные вероятности появления объектов соответствующих классов – P (Q^A1_i);

ü условные плотности распределения значений признаков по классам, т.е. функции f(X/Q_m) или f_Qi^A1(x1,…,xⁿ_a), i=1,..,m, j=1,..,n.

Если признаков всего один, то f(X/Q_m) – одномерная функция.

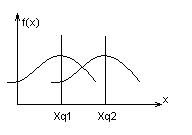
Если параметров много, то f(X/Q_m) – многомерная. Пример для 2-х мерной функции:

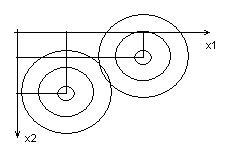
7. Если объем исходной информации недостаточен для

непосредственного описания классов, то они могут быть получены с помощью процедуры обучения.

8. Наличие описаний классов в принципе позволяет определить

решающие правила (решающие границы или критерии), с помощью которых обеспечивается минимизация ошибок при распознавании неизвестных объектов.

9. Пусть 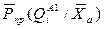- оценка апостериорной вероятности правильного

решения задачи распознавания, осредненная по всем возможным значениям признаков априорного словаря, описываемого вектором Ха (можно применить метод статистических испытаний – Монте – Карла). При этом переход от априорного словаря к рабочему (число априорных признаков больше или равно числу рабочих) происходит в условиях и из-за наличия ограничений на средства измерения. В том случае введем в рассмотрение вектор 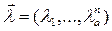, компоненты которого:

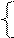l_j = 1, если признак внесен в словарь;

0, если j-го признака в словаре нет.

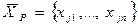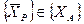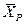10. Введем обозначение для рабочего словаря , где (f₁,…,f_n)Î1,…,n, т.е. множество признаков рабочего словаря состоит из элементов множества признаков априорного словаря, т.е. , где - подмножество признаков априорного словаря.

11. Обозначим через C_j стоимость создания измерительного устройства,

обеспечивающего определение Х_j–го признака, j=1,…,n, а через С₀ – общую величину ресурсов на создание всех измерителей.

Если 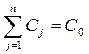, то используется в качестве рабочего априорный словарь – и никаких проблем!

Однако, для всех признаков в общем случае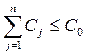

12. Затраты на создание комплекса технических средств системы ТРО:

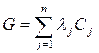
Обозначим через 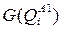- выигрыш от реализации возможных решений при распознавании объекта “w”, отнесенного к классу 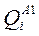в варианте классификации А1. Тогда математическое ожидание выигрыша от выбора варианта при использовании априорного словаря признаков равно:

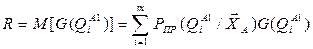
Величину R уместно распознавать как критерий эффективности системы, и с его увеличением (максимизацией) следует связать эффективность ее функционирования.

Правило: В условиях ограничений С₀ надо найти такой вариант разбиения объектов на классы и такое пространство признаков, при котором максимизируется критерий R, т.е. необходимо:

- определить 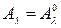из множества А={A₁,…,A_r} и такой вектор 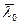, которые при наилучшем решающем правиле доставляют max R, C£С₀,

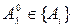
т.е.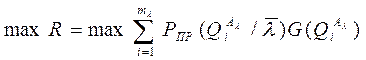

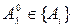
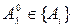i=1

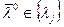
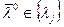
при ограничении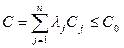

При том А⁰_l определяет оптимальный алфавит классов, а 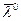- оптимальный рабочий словарь признаков, т.е. .

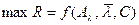Общая постановка проблемы распознавания:

В условиях априорного описания исходного множества объектов на языке априорного словаря признаков необходимо в пределах ресурсов определить оптимальный алфавит классов и оптимальный рабочий словарь признаков, который при наилучшем g_j обеспечивает максимум R.