Nbsp; Решение
ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ
Типовые примеры
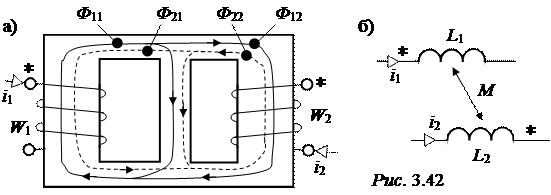 |
ЗАДАЧА 3.47. Выполнить разметку одноимённых (однополярных) зажимов в схеме рис. 3.42,а.
Обозначим верхний зажим первой катушки, имеющей число витков W1, значком *, оставив нижний зажим без наименования. Выбираем произвольное направление тока первой катушки i1 (на рисунке он направлен входящим в зажим со звёздочкой *).
Используя правило правой руки (или правило правоходового винта), укажем направление магнитного потока Ф11 самоиндукции первой катушки. Так как силовые линии магнитного поля замкнуты, покажем направление магнитного потока взаимной индукции Ф12 (индекс «1» - со стороны тока i1, индекс «2» - действие на вторую катушку).
Для того, чтобы найти одноимённый зажим (*) второй катушки, выби-раем произвольное направление тока относительно зажимов 2-ой катушки. Например, i2 входит в нижний зажим, и находим направления Ф22 и Ф21.
На схеме рис. 3.42,а получилось, что в каждой катушке магнитные по-токи самоиндукции и взаимной индукции вычитаются (направлены противо-положно). Следовательно, токи i1 и i2 по-разному ориентированы относитель-но однополярных зажимов, и зажим (*) у второй катушки находится вверху.
Заметим, что положение однополярных зажимов не зависит от выбранных направлений токов при их разметке, а определяется только конструкцией магнитопровода и направлениями намотки проводов катушек.
При дальнейшей работе со схемой, в которую включены катушки W1 и W2 схема рис. 3.42,а заменяется схемой рис. 3.42,б.
ЗАДАЧА 3.48. На рис. 3.43,а индуктивно связанные катушки соедине-ны в узле однополярными зажимами, на рис. 3.43,б те же катушки соединены в узле разнополярными зажимами. Определить показания вольтметра обеих схем, если: x1 = 20 Ом, x2 = 10 Ом, коэффициент связи катушек k = 0,5, ёмкостное сопротивление x3 = 10 Ом, ЭДС e(t) = 100 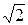 sin(wt) B.
sin(wt) B.
nbsp; Решение
Выполним расчёты в комплексной форме. Комплексная ЭДС источника питания обеих схем E = E×e jye = 100 B.
Сопротивление вольтметра бесконечно велико, поэтому ток i2 = 0в обеих схемах, а комплексы токов I1 = I3 = 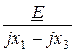 =
= 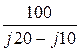 = -j10 A.
= -j10 A.
Напряжение UM = I1×jxM, наводимое изменяющимся током I1 во второй катушке, имеет то же направление относительно однополярных зажимов, что и ток I1, что отражено на схемах рис. 3.43,а и 3.43,б. Сопротивление взаимной индукции xM = k×  = 0,5
= 0,5 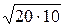 = 5
= 5 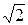 Ом.
Ом.
Напряжение на зажимах вольтметра рассчитаем с помощью II закона Кирхгофа. Для схемы рис. 3.43,а UV – I3×(-jx3) – UM = 0, откуда
UV = (-j10)×(-j10) + (-j10)×j5 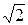 = -100 + 10×7,07 = -29,3 B, а показание вольтметра UV = 29,3 B.
= -100 + 10×7,07 = -29,3 B, а показание вольтметра UV = 29,3 B.
Для схемы рис. 3.43,б UV – I3×(-jx3) + UM = 0, откуда
UV = (-j10)×(-j10) – (-j10)×j5 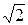 = -100 – 10×7,07 = -170,7 B, а показание вольтметра UV = 170,7 B.
= -100 – 10×7,07 = -170,7 B, а показание вольтметра UV = 170,7 B.
Отметим, что эта задача иллюстрирует способ практической маркировки одноимённых зажимов обмоток трансформатора. Достаточно сравнить показания вольтметра для двух случаев включения вторичной обмотки трансформатора и сделать соответствующие выводы.
ЗАДАЧА 3.49. Параметры схемы рис. 3.44,а r1 = 10 Ом, x1 = 20 Ом, r2 = 40 Ом, x2 = 30 Ом, xM = 20 Ом, приложенное напряжение U = 220 B. Найти показания приборов. Построить векторную диаграмму цепи. Записать уравнение баланса мощностей. Найти активную мощность, передаваемую из 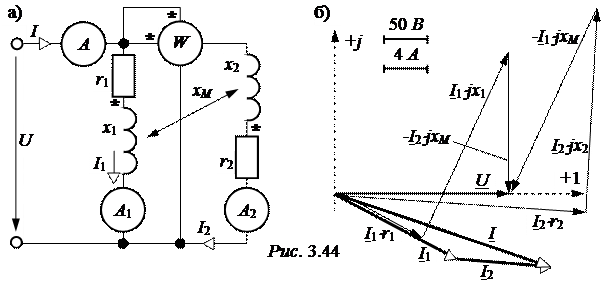 одной ветви в другую.
одной ветви в другую.
Решение
Примем U = 220 B.
Комплексные сопротивления ветвей
Z1 = r1 + jx1 = 10 + j20 Ом, Z2 = r2 + jx2 = 40 + j30 Ом, ZM = jxM = j20 Ом.
Для расчёта токов воспользуемся системой уравнений Кирхгофа:
I = I1 + I2; I1×Z1 – I2×ZM = U; I2×Z2 – I1×ZM = U.
решая систему двух последних уравнений методом Крамера, получаем:
I1 = U× 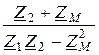 =
= 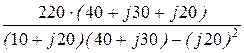 =12,6×e -j28,36°=11,09-j5,99 A;
=12,6×e -j28,36°=11,09-j5,99 A;
I2 = U× 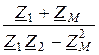 =
= 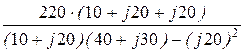 = 8,11×e –j3,74°=8,09-j0,53 A;
= 8,11×e –j3,74°=8,09-j0,53 A;
I = 11,09 – j5,99 + 8,09 – j0,53 = 19,18 – j6,52 = 20,26×e –j18,77° A.
Проверим балансы мощностей. Мощность источника питания
SГ = PГ + jQГ = U× 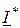 = 220×(19,18 + j6,52 ) = 4220 + j1434 BA.
= 220×(19,18 + j6,52 ) = 4220 + j1434 BA.
Суммарная активная мощность потребителей
SРП = I12×r1 + I22×r2 = 12,62×10 + 8,112×40 = 4219 Вт,
суммарная реактивная мощность
SQП = I12×x1 + I22×x2 - 2×I1×I2×xM×cos(yi1 - yi2) =
= 12,62×20 + 8,112×30 - 2×12,6×8,11×20×cos(-28,36°+3,74°) = 1433 вар.
Так как оба баланса мощностей выполняются, задача расчёта токов решена верно.
Отметим, что слагаемое реактивной мощности
-2×I1×I2×xM×cos(yi1 - yi2) = -3716 вар
определяет расход реактивной мощности для создания магнитного потока передачи активной мощности, а знак «минус» этой мощности указывает на взаимное ослабление (размагничивание) потоками взаимной индукции потоков самоиндукции (см. рис. 3.42).
Показание ваттметра РW = Re(U× 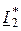 )= Re[220×(8,09+j0,53 )] = 1780 Вт.
)= Re[220×(8,09+j0,53 )] = 1780 Вт.
Ваттметр измеряет активную мощность, поступающую «электриче-ским путём» во вторую ветвь: Р2пост = Re(U× 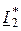 )= 1780 Вт.
)= 1780 Вт.
Потребляемая активная мощность определяется законом Джоуля-Ленца Р2П = I22×r2 = 8,112×40 = 2631 Вт.
Разность этих мощностей передаётся магнитным полем в первую ветвь
Р2®1 = Р2пост – Р2П = 1780 – 2631 = -851 Вт.
Знак «минус» в полученном результате указывает на то, что в действительности имеет место передача активной мощности из первой ветви во вторую (Р1®2 = +851 Вт) на покрытие дефицита мощности (потребление больше поступления).
Заметим, что есть другой путь подсчёта передаваемой активной мощности:
Р1®2 = -I1×I2×xM×sin(yi1– yi2) = -12,6×8,11×20×sin(-28,36° + 3,74°) = +851 Вт.
Для построения векторной диаграммы сначала на комплексной плоскости откладываем векторы (комплексы) токов I1 и I2 (рис. 3.44,б). Затем рассчитываем падения напряжений
I1×r1 = 12,6×10 = 126 В, I1×x1 = 12,6×20 = 252 В, I2×xM = 8,11×20 = 162,2 В,
I2×r2 = 8,11×40 = 324,4 В, I2×x2 = 8,11×30 = 243,3 В, I1×xM = 12,6×20 = 252 В.
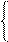 От начала координат выполняем операции сложения векторов (соответствующих комплексных чисел) в соответствии с исходной системой уравнений Кирхгофа: I1×r1 + I1×jx1 – I2×jxM = U,
От начала координат выполняем операции сложения векторов (соответствующих комплексных чисел) в соответствии с исходной системой уравнений Кирхгофа: I1×r1 + I1×jx1 – I2×jxM = U,
I2×r2 + I2×jx2 – I1×jxM = U.
Векторная диаграмма приведена на рис. 3.44,б.
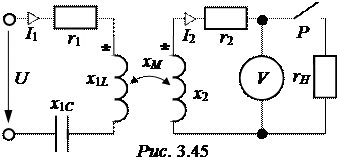
ЗАДАЧА 3.50. При разомк-нутом рубильнике Р показание вольтметра в схеме рис. 3.45 составляет 150 В. Параметры схе-мы r1 = 12 Ом, x1L = 10 Ом,
x1C = 26 Ом, r2 = 4 Ом, x2 = 20 Ом, rН = 12 Ом, U = 300 B.
Найти токи в схеме при замкнутом рубильнике, построить векторную диаграмму цепи.
Решение
Определим xM из условия, что при разомкнутом рубильнике I2Х = 0 – холостой ход однофазного трансформатора схемы.
I1Х = 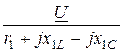 =
= 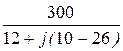 = 15×e j53,13° A;
= 15×e j53,13° A;
U2Х = I1Х ×xM - показание вольтметра, откуда xM = 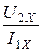 =
= 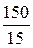 = 10 Ом.
= 10 Ом.
Проверим соотношение, вытекающее из физики явления взаимной индукции xM £  : 10 <
: 10 < 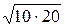 – выполняется.
– выполняется.
При замкнутом рубильнике в соответствии со II законом Кирхгофа для первичного и вторичного контуров трансформатора получаем
I1×Z1 – I2×ZM = U; I2×Z2 – I1×ZM = 0,
где комплексное сопротивление первичного контура
Z1 = r1 + jx1L – jx1C = 12 – j16 Ом,
вторичного контура Z2 = r2 + rН + jx2 = 16 + j20 Ом,
сопротивление ZM = jxM = j10 Ом,
комплексное напряжение U = 300 B.
Решая систему уравнений, получаем:
I1 = 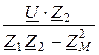 =
= 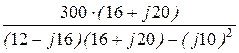 = 12,55×e j52,83°= 7,582 + j10 A;
= 12,55×e j52,83°= 7,582 + j10 A;
I2 = 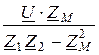 =
= 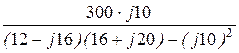 = 4,9×e j91,5°= -0,128 + j4,9 A.
= 4,9×e j91,5°= -0,128 + j4,9 A.
Проверим балансы мощностей по результатам расчёта токов.
SГ = PГ + jQГ = U× 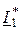 = 300×(7,582 – j10) = 2275 – j3000 BA.
= 300×(7,582 – j10) = 2275 – j3000 BA.
Суммарная активная мощность потребителей
SРП = I12×r1 + I22×(r2 + rН) = 12,552×10 + 4,92×16 = 2274 Вт » PГ.
Суммарная реактивная мощность
SQП = I12×(x1L - x1C) + I22×x2 - 2×Im(I2×jxM × 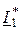 ) =
) =
= 12,552×(10 - 26) + 4,92×20 – 2×Im(4,9×e j91,5°×10×e j90°×12,55×e -j52,83°)=
= -2040 – 2×Im(615×e j128,67°) = -2040 – 960 = -3000 вар = QГ.
Отметим, что у трансформатора нет «электрического» канала передачи энергии из первичной обмотки во вторичную, поэтому передача активной мощности осуществляется только магнитным полем, и должно выполняться равенство Р1®2 = -Re(I2×jxM × 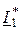 ) = I22×(r2 + rН).
) = I22×(r2 + rН).
Проверим:
Р1®2 = -Re(4,9×e j91,5°×10×e j90°×12,55×e -j52,83°) = -Re(615×e j128,67°) = 384,3 Вт »
» 4,92×16 = 384,2 Вт.
Показание вольтметра при замкнутом рубильнике
UV = I2×rН = 4,9×12 = 58,8 В.
Для построения векторной диаграммы рассчитаем падения напряжений: I1×r1 = 12,55×12 = 150,6 В; I1×x1L = 12,55×10 = 125,5 В;
 |
I1×x1C = 12,55×26 = 326,3 В; I2×xM = 4,9×10 = 49 В;
I2×r2 = 4,9×4 = 19,6 В; I2×x2= 4,9×20 = 98 В;
I2×rН = 4,9×12 = 58,8 В; I1×xM = 12,55×10 = 125,5 В.
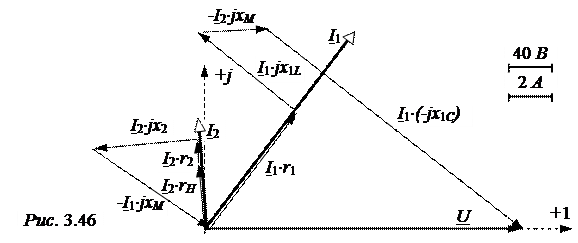
Построение векторной диаграммы начинаем с построения векторов токов I1 и I2 на комплексной плоскости в соответствии с рассчитанными комплексами (рис. 3.46).
Векторы падений напряжений откладываются в соответствии с законом Кирхгофа для контуров I1×r1 + I1×jx1L – I2×jxM + I1×(-jx1C) = U;
I2×rН + I2×r2 + I2×jx2 – I1×jxM = 0.
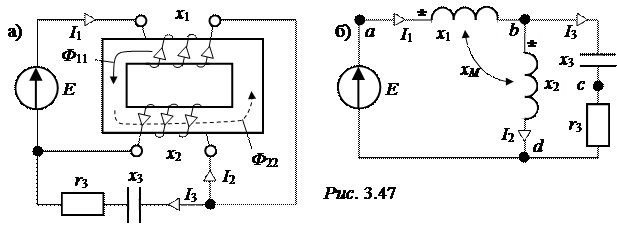
ЗАДАЧА3.51. Рассчитать состояние цепи с автотрансформатором (рис. 3.47,а), найти передаваемую активную мощность магнитным полем, построить векторную диаграмму цепи, если
x1 = 40 Ом, x2 = 80 Ом, xM = 50 Ом, r3 = 40 Ом, x3 = 20 Ом, E = 220 B.
Решение
После разметки однополярных зажимов с помощью потоков Ф11 и Ф22 расчётная схема электрической цепи приобретает вид рис. 3.47,б, на основа-
нии законов Кирхгофа состояние которой определяет система уравнений
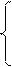 I1 = I2 + I3;
I1 = I2 + I3;
I1×jx1 + I2×jxM + I3×(-jx3) + I3×r3 = E;
I2×jx2 + I1×jxM – I3×(-jx3) – I3×r3 = 0.
 |
В соответствии с этой системой уравнений будет построена векторная диаграмма исходной цепи.
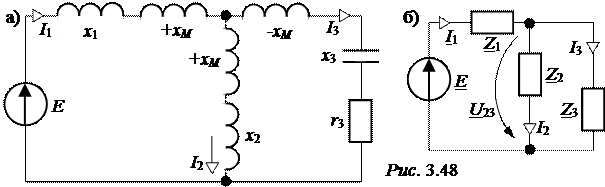 |
Чтобы избежать решения системы представленных уравнений, устра-ним взаимную индуктивную связь, получив эквивалентную схему рис. 3.48,а и соответствующую ей комплексную схему замещения (рис. 3.48,б).
«Развязка» осуществляется по следующему правилу: если индуктивно связанные элементы x1 и x2 сходятся в узел b разнополярными зажимами, то последовательно к индуктивным элементам вводятся положительные расчётные индуктивности +xM = +wM, а в общую для x1 и x2 часть схемы (в рассматриваемом примере это ветвь №3) вводится отрицательное расчётное индуктивное сопротивление -xM = -wM.
Примем комплексную ЭДС схемы рис. 3.48,б E = E× 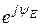 = 220 B.
= 220 B.
Комплексные сопротивления смешанно соединённых ветвей
Z1 = jx1 + jxM = j40 + j50 = j90 Ом,
Z2 = jx2 + jxM = j80 + j50 = j130 Ом,
Z3 = r3 – jx3– jxM = 40 – j20 – j50 = 40 – j70 = 80,62×e –j60,25° Ом.
Входное сопротивление цепи
Zвх = Z1 + 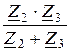 = j90 +
= j90 + 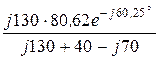 = 132,4×e j10,89° Ом,
= 132,4×e j10,89° Ом,
а сопротивление разветвления
Z23 = 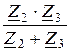 =
= 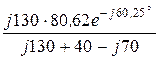 = 145,3×e –j26,56° Ом.
= 145,3×e –j26,56° Ом.
Входной ток I1 = 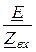 =
= 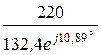 = 1,662×e –j10,89° А,
= 1,662×e –j10,89° А,
напряжение на разветвлении
U23 = I1×Z23 = 1,662×e –j10,89°× 145,3×e –j26,56° = 241,5×e –j37,45° В,
токи параллельных ветвей I2 = 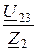 =
= 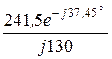 = 1,858×e –j127,45° А,
= 1,858×e –j127,45° А,
I3 = 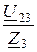 =
= 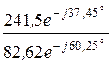 = 3,0×e j22,8° А.
= 3,0×e j22,8° А.
Чтобы убедиться в правильности расчёта токов исходной схемы рис. 3.47,а, проверим для неё балансы активных и реактивных мощностей:
- мощность генератора
SГ = Е× 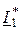 = 220×1,662×e j10,89° = 359 + j69,1 BA = PГ + jQГ.
= 220×1,662×e j10,89° = 359 + j69,1 BA = PГ + jQГ.
- активная мощность потребителей
SРП = I32×r3 = 32×40 = 360 Вт » PГ,
- реактивная мощность потребителей
SQП = I12×x1 + I22×x2 + 2×I1×I2×xM×cos(yi1 – yi2) – I32×x3 =
= 1,6622×40 + 1,8582×80 + 2×1,662×1,858×50×cos(-10,89°+127,45°) – 32×20 =
= 110,5 + 276,2 – 138,1 – 180 = 68,6 вар » QГ.
Передаваемая активная мощность из первой ветви во вторую
Р1®2 = Re(I2×jxM × 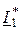 ) = I1×I2×xM×sin(yi1 – yi2) =
) = I1×I2×xM×sin(yi1 – yi2) =
= 1,662×1,858×50×sin(-10,89°+127,45°) = 138,1 Вт.
Обращаем внимание на то, что потребляемые активные мощности пер-
вой и второй ветвей схемы с автотрансформатором Р1П = Р2П = 0, так как активные сопротивления обмоток автотрансформатора r1= r2= 0 и в них отсутствуют тепловые потери.
Напряжение на участке ab схемы рис. 3.47,б
Uab = I1×jx1 + I2×jxM = 1,662×e –j10,89°×40×e j90° + 1,858×e –j127,45°×50×e j90° =
= 86,76×e j5,83° B,
на участке bd
Ubd = I2×jx2 + I1×jxM = I3×(r3 – jx3) = 3×e j22,8°×(40 – j20) = 134,2×e –j3,77° B.
Поступающая мощность в первую обмотку (участок ab)
S1пост = Uab × 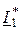 = 86,76×e j5,83°×1,662×e j10,89° = 138,1 + j41,5 BA = P1пост + jQ1пост.
= 86,76×e j5,83°×1,662×e j10,89° = 138,1 + j41,5 BA = P1пост + jQ1пост.
Так как тепловые потери на этом участке схемы отсутствуют, то вся поступающая активная мощность P1пост должна передаваться во вторую ветвь Р1®2 = P1пост – I12×r1 = 138,1 – 0 = 138,1 Вт,
что проверяется следующим образом:
S2пост =Ubd × 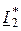 = 134,2×e –j3,77°×1,858×e j127,45°= -138,1+j207,5 BA = P2пост + jQ2пост.
= 134,2×e –j3,77°×1,858×e j127,45°= -138,1+j207,5 BA = P2пост + jQ2пост.
так как P2п = I22×r2 = 0, то передаваемая активная мощность из второй ветви в первую Р2®1 = P2пост – P2п= -138,1 – 0 = -138,1 Вт
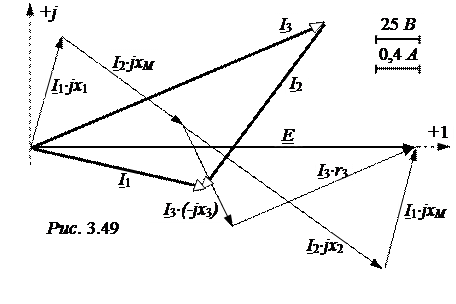 и сумма Р1®2 + Р2®1 = 138,1 – 138,1 = 0.
и сумма Р1®2 + Р2®1 = 138,1 – 138,1 = 0.
Для построения
векторной диаграммы
полезно найти падения
напряжений, связанные
с токами схемы:
I1×x1=1,662×40 = 66,5 В;
I2×xM =1,858×50 = 92,9 В;
I2×x2=1,858×80 =150,6 В;
I1×xM =1,662×50 = 83,1 В;
I3×x3= 3×20 = 60 В;
I3×r3 = 3×40 =19,6 В,
а токи представить в алгебраической форме
I1 = 1,63 – j0,31 A;
I2 = -1,13 – j1,47 A;
I3 = 2,76 + j1,16 A.
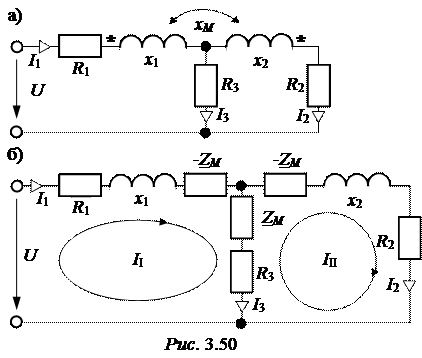
На комплексной плоскости (рис. 3.49) строим векторы токов в соответствии с I законом Кирхгофа по исходной системе урав-нений, а затем откладываем векторы падений напряжений в соответствии с исходными уравнениями, записанными по II закону Кирхгофа.
ЗАДАЧА 3.52. В схеме рис. 3.50,а рассчитать токи, если U = 100 B, r1 = 5 Ом, r2 = 15 Ом, r3 = 10 Ом, x1 = 15 Ом, x2 = 25 Ом, xM = 10 Ом.
Решение
Задачу решим методом контурных токов, предварительно «развязав» индуктивно связанные элементы (рис. 3.50,б). Система уравнений:
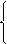 II×(R1 + jx1 – jxM +jxM + R3) – III×(R3 + jxM) = U;
II×(R1 + jx1 – jxM +jxM + R3) – III×(R3 + jxM) = U;
-II×(R3 + jxM) + III×(R3+jxM – jxM + jx2 + R2) = 0.
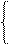 II×(15 + j15) – III×(10 + j10) = 100;
II×(15 + j15) – III×(10 + j10) = 100;
-II×(10 + j10) + III×(25+j25) = 0.
Решение системы методом Крамера:
D = j550; DI = 2500 + j2500; DII = 1000 + j1000;
II = DI/D = 6,43×e –j45° A; III = DII/D = 2,57×e –j45° A.
Токи в ветвях через контурные токи определяем по принципу наложения:
I1 = II = 6,43×e –j45° A; I2 = III = 2,57×e –j45° A; I3 = II - III = 3,87×e –j45° A.
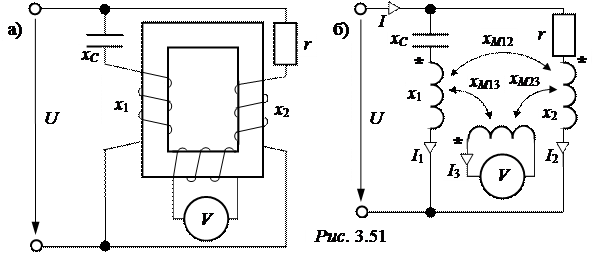
ЗАДАЧА3.53. В схеме рис. 3.51,а рассчитать токи, построить вектор-ную диаграмму, найти активную мощность, передаваемую из первой обмот-ки во вторую, показание вольтметра. Определить входное сопротивление цепи по закону Ома и путём «развязки» индуктивной связи. Числовые данные: U =100 B, xС = x1 = 20 Ом, x2 = 10 Ом, r =10 Ом, xM12 = xM23 =10 Ом, xM13 = 5 Ом.
Решение
Определяем одноимённые зажимы обмоток и составляем расчётную схему (рис. 3.51,б). Задачу решаем методом уравнений Кирхгофа. Учитываем, что сопротивление вольтметра ZV =¥, поэтому ток в третьей обмотке I3 = 0. Таким образом, ток I3 влияния не оказывает и в уравнениях не учитывается. Система уравнений имеет вид:
I = I1 + I2; (1)
I1×(-jxC + jx1) + I2×jxM12= U; (2)
I1×jxM12+ I2×(r +jx2) = U; (3)
I1×jxM13+ I2×jxM23= UV ; (4)
Решаем уравнения (2) и (3) относительно I1 и I2:
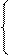
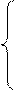 I1×0 + I2×j10= 100; I2= 100/j10 = -j10 A;
I1×0 + I2×j10= 100; I2= 100/j10 = -j10 A;
I1×j10 + I2×(10 + j10) = 100; I1 = 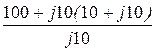 = 10 A.
= 10 A.
Из (1) I = 10 + (-j10) = 14,14×e -j45° A.
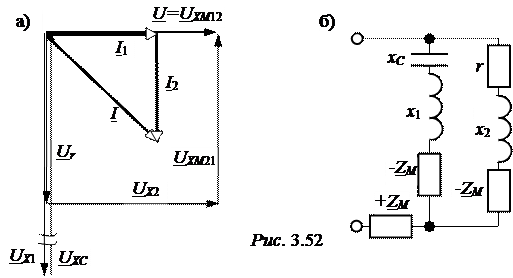
Для построения векторной диаграммы (рис. 3.52,а) найдём падения напряжения на всех элементах:
UC = I1×(-jxC) = 10×(-j20) = -j200 B; Ur = I2×r = -j10×10 = -j100 B;
UX1= I1×jx1 = 10×j20 = j200 B; UX2= I2×jx2 = -j10×j10 = 100 B;
 |
UXM12= I2×jxM12 = -j10×j10 = 100 B; UXM21= I1×jxM12 = 10×j10 = j100 B.
Активная мощность, потребляемая первой ветвью
P1 = Re(U× 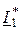 ) = Re(100×10) = 1000 Bт.
) = Re(100×10) = 1000 Bт.
Расход активной мощности в первой ветви DP1 = r1×I12 = 0.
Передаваемая магнитным полем из первой ветви во вторую активная мощность Р1®2 = P1– DP1= 1000 – 0 = 1000 Bт.
Напряжение на вольтметре по (4)
UV = 10×j5+ (-j10)×j10 = j50+ 100 = 111,8×e j26,6° В.
Показание вольтметра V ® UV = 111,8 В.
Входное сопротивление цепи по закону Ома
Z = 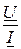 =
= 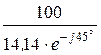 = 7,07×e j45° Ом.
= 7,07×e j45° Ом.
После «развязки» индуктивной связи получаем схему рис. 3.52,б. Здесь
ZM = jxM12 = j10 Ом.
Входное сопротивление цепи
Z = ZM + 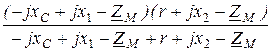 =
=
= j10 + 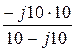 = j10 + 5 – j5 = 7,07×e j45° Ом.
= j10 + 5 – j5 = 7,07×e j45° Ом.
 |
Ответ тот же, что и при определении по закону Ома.
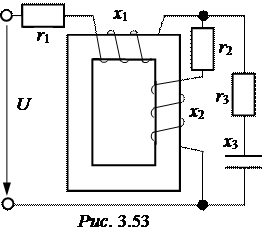 ЗАДАЧА3.54. В схеме рис. 3.53 составить систему уравнений методом законов Кирхгофа. Выполнить расчёт токов путём «развязки» индуктивной связи. Определить токи методом контурных токов. Определить мощность, передаваемую магнитным путём из первой катушки во вторую. Числовые данные:
ЗАДАЧА3.54. В схеме рис. 3.53 составить систему уравнений методом законов Кирхгофа. Выполнить расчёт токов путём «развязки» индуктивной связи. Определить токи методом контурных токов. Определить мощность, передаваемую магнитным путём из первой катушки во вторую. Числовые данные:
U = 220 B, r1 = 6 Ом, x1 = 10 Ом,
r2 = 12 Ом, x2 = 18 Ом, r3 = 18 Ом,
x3 = 20 Ом, xM = 8 Ом.
Решение
1. Составим расчётную схему (рис. 3.54,a). Система уравнений для токов по законам Кирхгофа:
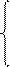 I1 – I2 – I3 = 0;
I1 – I2 – I3 = 0;
r1×I1+jx1×I1+jxM ×I2+r2×I2+jx2×I2+jxM×I1= U;
-r2×I2– jx2×I2– jxM ×I1+ r3×I3 – jx3×I3= 0.
 |
2. Выполним «развязку» индуктивной связи (рис. 3.54,б) и рассчитаем полученную схему.
Z1 = r1 + jx1+ jxM = 6 + j18 =18,97×e j71,6° Ом,
Z2 = r2 + jx2 + jxM =12 + j26 = 28,64×e j65,2° Ом,
Z3 = r3 – jx3– jxM =18 – j28 = 33,29×e –j57,3° Ом.
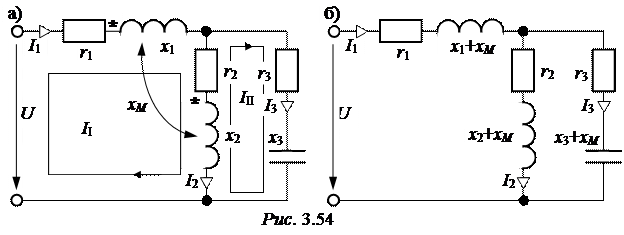
Z23 = 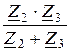 =
= 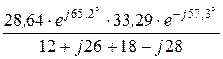 = 31,70×e j11,8° = 31,04 + j6,47 Ом.
= 31,70×e j11,8° = 31,04 + j6,47 Ом.
Входное сопротивление цепи
Zвх = Z1 + Z23 = 6 + j18 + 31,04 + j6,47= 37,04 + j24,47= 44,39×e j33,5° Ом.
I1 = 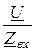 =
= 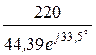 = 4,96×e –j33,5° А,
= 4,96×e –j33,5° А,
I2 = I1× 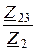 = 4,96×e –j33,5°×
= 4,96×e –j33,5°× 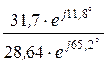 = 5,49×e –j86,9° А,
= 5,49×e –j86,9° А,
I3 = I1× 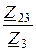 = 4,96×e –j33,5°×
= 4,96×e –j33,5°× 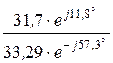 = 4,72×e j35,6° А.
= 4,72×e j35,6° А.
3. Система уравнений по методу контурных токов:
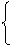 (r1 + jx1 + r2 + jx2 + j2xM)×II – (r2 + jx2 + jxM)×III = U;
(r1 + jx1 + r2 + jx2 + j2xM)×II – (r2 + jx2 + jxM)×III = U;
-(r2 + jx2 + jxM)×II +( r2 + jx2 + r3 – jx3)×III = 0;
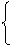 (18 + j44)×II – (12 + j26)×III = 220;
(18 + j44)×II – (12 + j26)×III = 220;
-(12 + j26)×II +(30 – j2)×III = 0.
Её решение II = 4,96×e –j33,5° А, III = 4,72×e j35,6° А.
Токи в ветвях: I1 = II = 4,96×e –j33,5° А, I3 = III = 4,72×e j35,6° А,
I2 = II - III = 4,96×e –j33,5° – 4,72×e j35,6° = 5,49×e –j86,9° А.
4. Активная мощность, передаваемая магнитным путём из первой катушки во вторую:
Р1®2 = xM ×I1×I2× sin(yi1 – yi2) = 8×4,96×5,49×sin(-33,5°+86,9°) = 174,9 Вт.
Дата добавления: 2016-01-18; просмотров: 2321;
