Применение ПЭВМ для расчёта цепей со взаимной индуктивностью
ЗАДАЧА 3.63. В схеме рис. 3.55 рассчитать токи во всех ветвях цепи, если Е1= 220 B, Е2= 220×e j120° B, J = -j5 A, Z1 = 10 + j10 Ом, Z2 = 20 + j30 Ом, Z3 = 40 – j15 Ом, M12 = 31 мГн, М13 = 50 мГн, М23 = 70 мГн. Частота 50 Гц. Составить баланс мощностей.
Программа решения задачи в системе MathCAD
Исходные данные
j:=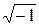 
Е1:= 220 Е2:= 220×e j×120×deg J := -j×5 ORIGIN:= 1
Z1 := 10 + j×10 Z2 := 20 + j×30 Z3 := 40 – j×15
M12 := 0.031 М13 := 0.05 М23 := 0.07
Решение
Определим величины сопротивлений взаимной индукции
w := 100×p ZM12 := j×w×M12 ZM13 := j×w×M13 ZM23 := j×w×M23
Расчёт токов произведём методом контурных токов (см. рис. 3.55) с учётом того, что третий контурный ток равен току источника J.
Матрицы контурных сопротивлений и контурных ЭДС
Zk :=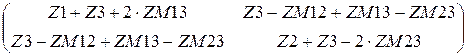 
Ek :=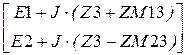 
Контурные токи Ik := Zk -1×Ek Ik =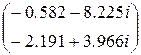 
Токи ветвей I1 := Ik1 I2 := Ik2 I3 := - J + Ik1 + Ik2
I1 = -0.582 – 8.225i I2 = -2.191 + 3.966i I3 = -2.773 + 0.741i
Мощность источников Si := E1·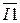 
+ E2· 
+ 
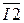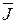·(-I3·Z3 – I1·ZM13 + I2·ZM23)
Si = 1.42´103 + 1.245i´103
Напряжения взаимоиндукции на индуктивно связанных элементах
UM1 := -I2·ZM12 + I3·ZM13 UM2 := -I1·ZM12 – I3·ZM23
UM3 := I1·ZM13 – I2·ZM23
Реактивная мощность взаимоиндукции
SM := UM1· 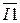+ UM2· 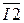+ UM3· 
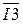SM = 73.123i
Мощность приёмников
Spr := (|I1|)2·Z1 + (|I2|)2·Z2 + (|I3|)2·Z3 + SM Spr = 1.42´103 + 1.245i´103
Баланс мощностей Si = Spr выполняется.
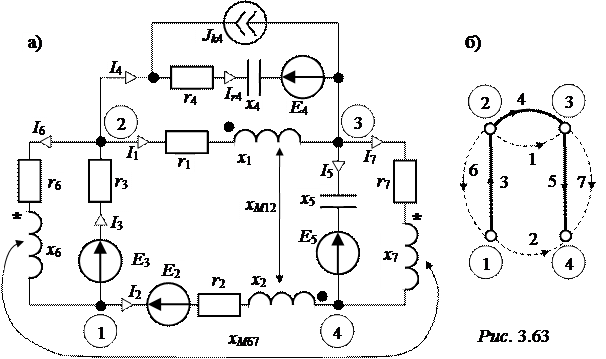
ЗАДАЧА 3.64. Рассчитать токи в схеме рис. 3.63,а, если e2(t) = = 200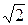 
×sin(wt - 30°) B, e3(t) = 100 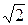×sin(wt - 90°) B, e4(t) = 150 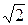×sinwt B, e5(t) = 250 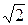×sin(wt + 45°) B, jk4(t) = 8 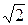×sin(wt + 90°) A, r1 = 10 Ом, x1 = =15 Ом, r2 = 30 Ом, x2 = 20 Ом, xM12 = 12 Ом, r3 = 25 Ом, r4 = 16 Ом, x4 = =12 Ом, x5 = 40 Ом, r6 =14 Ом, x6 =18 Ом, r7 = 24 Ом, x7 =16 Ом, xM67 =13 Ом.
Решение
Выбираем произвольные направления токов в ветвях (указаны на рис. 3.63,а) и строим граф схемы (рис. 3.63,б).
Обратим внимание на то, что в приведенной схеме есть одна обобщённая ветвь №4 с током ветви i4 и током сопротивления ветви ir4.
Примем за базисный узел №4 с комплексным потенциалом j 4 = 0. В приведенной схеме три узла с неизвестными потенциалами и четыре главных контура. В этом случае рациональнее решать задачу расчёта токов методом узловых потенциалов.
Используем ПЭВМ для формирования и решения расчётных уравнений.
Программа решения задачи в системе MathCAD
ORIGIN := 1 j :=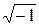
Сопротивления
Z1 := 10 + j×15 Z2 := 30 + j×20 Z3 := 25 Z4 := 16 – j×12 Z5 := -j×40
Z6 := 14 + j×18 Z7 := 24 + j×16 ZM12 := j×12 ZM67 := j×13
Источники
Е2:= 200×e -j×30×deg Е3:= 100×e -j×90×deg Е4:= 150 Е5:= 250×e j×45×deg J4 := j×8
Матрицы ЭДС и источников тока ветвей
Е :=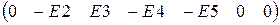 
J :=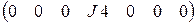 
Матрицы сопротивлений ветвей (Z), соединений (A) и главных контуров (B)
Z :=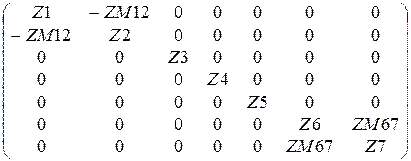 
A :=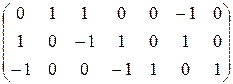 
Матрицы проводимостей, суммарных узловых токов и потенциалов узлов Y := A×Z-1×AT Jc := A×JT - A×Z-1×ET j := Y-1×Jc
 |
j =
Токи ветвей I := -JT + Z-1×(AT×j + ET) I =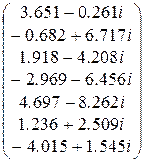 
Проверка баланса мощностей
Дата добавления: 2016-01-18; просмотров: 712;