Автокорреляционная функция и ее применение.

Автокорреляционная функция (АКФ) характеризует степень корреляционной связи между отдельными значениями наблюдений, представленными в виде случайного процесса и расположенными на некотором удалении друг от друга.

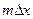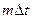Применительно к геофизическим данным АКФ представляет характеристику связи между значениями поля, отстоящими друг от друга на m- дискретов, т.е. дискретов по x или по t. АКФ является функцией аргумента или , где 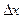- шаг по профилю, 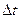- шаг по трассе сейсмограммы, т.е. .

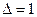АКФ рассчитывается по формуле:

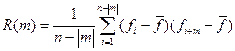(4.1)

где 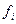- значение поля в i-той точке профиля (трассы, скважины); n – число точек наблюдений; m – интервал, принимающий последовательно значения 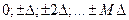, которые выражают расстояния между значениями поля 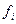и 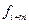; 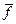- среднее значение поля по профилю, трассе и т.д.

Для m=1, сумма в выражении 4.1 представляет собой сумму произведений центрированных[3], значений поля соседних точек профиля:

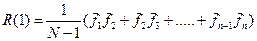(4.2)

здесь 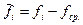, то есть центрированное значение поля на i - ом пикете профиля;

Для m=2, сумма в выражении 4.1 представляет собой сумму произведений центрированных значений поля, удаленных друг от друга на один пикет:

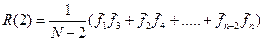(4.3)

Для любого m= k , (k<N) имеем:

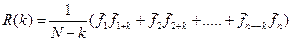(4.4)

По построению АКФ является четной функцией, т.е. 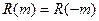. Ввиду четности АКФ обычно рассчитывается лишь для .

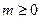При 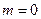значение АКФ представляет собой оценку дисперсии изучаемого поля, при 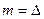АКФ выражает связь значений поля для соседних пикетов (дискретов) и представляет собой оценку коэффициента корреляции для этих значений, при 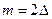АКФ выражает связь между значениями поля, отстоящими друг от друга на два дискрета и т.д.

На практике часто используются нормированные значения автокорреляционных функций R_н.(m). При этом нормирование осуществляется на R(0):

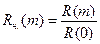(4.5)

Можно показать, что оценка нормированных значений автокорреляционной функции, при достаточном объеме выборки (количестве точек на профиле[4]) обладает следующими свойствами:

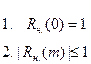(4.6)

3. Автокорреляционная функция является четной, то есть R_н.(m)= R_н.(-m), поэтому при оценках автокорреляционных функций обычно ограничиваются ее значениями для неотрицательных значений аргумента m>=0.

4.Два случайных процесса F₁={f₁, f₂,…..f_n} и F₂={kf₁, kf₂,…..kf_n} отличающиеся только постоянным множителем k, имеют один и тот же вид нормированной автокорреляционной функции R_н(m).

5.Два случайных процесса F₁={f₁, f₂,…..f_n} и F₂={f₁+k, f₂+k,…..f_n+k} смещенные относительно друг друга на постоянную величину k, имеют один и тот же вид нормированной автокорреляционной функции R_н(m).

Анализируя выражения 4.1 и 4.5 можно сделать вывод о том, что нормированные значения автокорреляционной функции R_н.(m) есть не что иное, как коэффициент корреляции, рассчитанный для точек удаленных друг от друга на m пикетов. Таким образом, значения корреляционной функции, для конкретного аргумента m показывает насколько значения поля, удаленные друг от друга на m пикетов, коррелированны[5] между собой. Так, если R(5)=0.85, то это свидетельствует о том, что значения поля, удаленные друг от друга на 5 пикетов, в целом, достаточно коррелированны, если R(9)=0.05, то значения поля удаленные на 9 пикетов практически независимы (некоррелированны). Наконец, если, например, R(13)=-0.9, то между значениями поля, отстоящими друг от друга на 13 пикетов, существует сильная обратная корреляционная связь. Случайный процесс, для которого даже при единичном смещении R(1)<=0 , получил название абсолютно некоррелируемого процесса (“белый шум”).

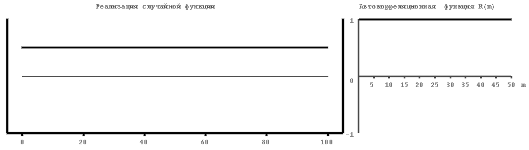
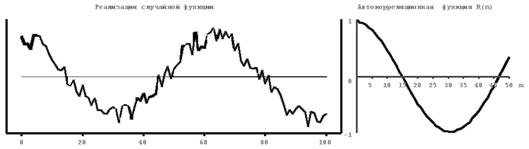
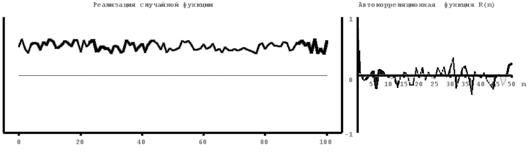
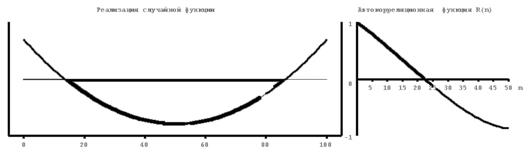
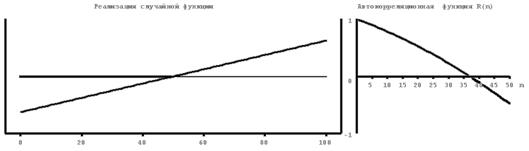
На рисунке 4.1 приведены примеры расчета нормированных автокорреляционных функций для различных случайных процессов, близких по форме к константе (1), синусоиде (2), абсолютно некоррелируемому процессу (3), квадратичной (4) и линейной (5) функциям. Из второго рисунка следует, что автокорреляционная функция периодического процесса является также периодической. При этом период автокорреляционной функции совпадает с периодом процесса. Для абсолютно некоррелируемого сигнала значения автокорреляционной функции близки к нулю при любых значениях аргумента, отличных от нуля.

	Рис.4.1. Некоторые реализации случайных процессов (слева) и их автокорреляционные функции (справа). 1-константа, 2-косинусоида, осложненная помехой, 3- абсолютно некоррелируемый сигнал или «белый шум», 4 – парабола, 5-линейная функция.

Нормированные значения автокорреляционной функции постоянного процесса тождественно равны единице, так как при любых смещениях m значения случайного процесса полностью совпадают, то есть абсолютно коррелируемы.

По АКФ определяется такой важный атрибут, как интервал корреляции. Под интервалом или радиусом корреляции понимают такое расстояние между значениями поля r, начиная с которого значения поля 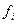и 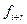можно считать некоррелированными, а при нормальном законе распределения – независимыми между собой. Для оценки интервала корреляции используются разные эвристические приемы. Наиболее распространенным приемом является оценка величины r по заданному значению 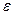, где 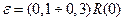. При этом r принимается равным аргументу АКФ, m, начиная с которого выполняется соотношение .

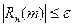Для оценки интервала корреляции используются также соотношения:

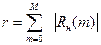или .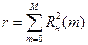

На практике, радиус корреляции оценивают по минимальному значение аргумента m, при котором автокорреляционная функция первый раз пересекает ось абсцисс.

Форма АКФ и интервал корреляции используются при решении различных задач обработки геофизических данных, из них выделим следующие:

1) Оценка корреляционных свойств сигналов и помех. При отсутствии корреляции между сигналом 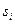помехой 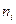, что обычно постулируется, т.е. появление сигнала не зависит от помехи, АКФ представляется суммой АКФ сигнала и АКФ помехи, поскольку :

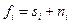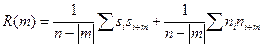
Из этого выражения следует, что при малой интенсивности помехи по сравнению с интенсивностью сигнала АКФ представляет оценку корреляционных свойств сигнала, и, наоборот, на интервале, где отсутствует сигнал, АКФ оценивает свойства помехи;

2) АКФ сигнала и помех является основой расчета всех оптимальных фильтров, рассматриваемых в главе VII;

3) При совпадении формы сигнала и формы АКФ помехи никакая дополнительная обработка по их разделению не внесет ничего нового, поскольку при этом частотные диапазоны сигнала и помехи полностью перекрываются между собой;

4) Разделение на однородные в статистическом отношении участки с целью геологического картирования. С этой целью используются обычно одновременно среднее значение, дисперсия и интервал корреляции, рассчитываемые в скользящих окнах;

5) Оценка разрешающей способности сейсмической записи по величине отношения 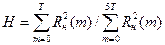, где Т - период записи. При Н, близком к единице, разрешающая способность велика, при Н£0,5 - низкая;

6) Использование интервала корреляции для оценки глубины залегания h объектов по потенциальным полям .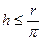

На этом простом соотношении между глубиной h и интервалом корреляции r, точно выполняемом для объектов в виде цилиндров бесконечного простирания, основаны приемы гравитационного, предложенного А.М.Петрищевским, и корреляционного, предложенного А.В.Петровым, зондирований потенциальных полей;

7) Оценка длительности реализации, например, длины профиля, для которой рассчитывается АКФ. В общем случае дисперсия АКФ определяется выражением 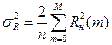, из которого следует возможность оценивания длительности самой реализации n.