Метод главных компонент при оценке региональной составляющей поля.

Выделение регионального тренда является распространенной процедурой обработки практически для всех методов геофизики. Однако при решении этой задачи приходится задавать те или иные параметры. Так, при осреднении поля в скользящем окне надо задать размеры окна, при пересчете поля на высоту надо задать высоту пересчета, при оценке региональной составляющей путем регрессии надо задать степень полинома регрессии и т.д.

Метод главных компонент не требует задания той или иной априорной информации. Единственное предположение, при котором происходит применение метода главных компонент, состоит в том, что региональная составляющая обладает наибольшей дисперсией по сравнению с локальными составляющими, что обычно на практике выполняется.

Алгоритм оценки региональной составляющей на основе метода главных компонент сводится к реализации следующих процедур:

1.Вычисление средних значений поля по каждому профилю 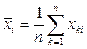, где n – число точек наблюдений, i=1,…….N, N – число профилей, и ковариаций данных различных пар профилей 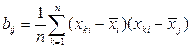, i,j=1,….N. Поскольку система x₁,….x_N представлена измерениями одного и того же поля, нет необходимости рассчитывать коэффициенты корреляции, которые используются при комплексном анализе данных, измеренных в разных физических единицах.

2.Составление ковариационной матрицы исходных данных по их коэффициентам ковариаций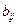

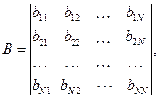
Матрица В симметрична относительно главной диагонали, т.е. 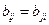, а по диагонали расположены дисперсии значений поля каждого профиля.

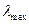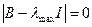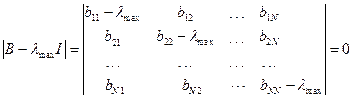3.Нахождение максимального собственного значения из уравнения или , т.е. после раскрытия определителя из этого уравнения достаточно найти его корень с максимальным значением .

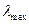4.Вычисление значений собственного вектора матрицы 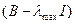, соответствующего максимальному собственному значению 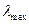из системы линейных уравнени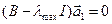й или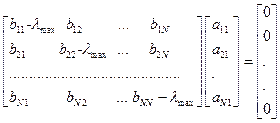

Значения собственного вектора 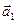определяются с учетом нормировки 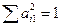. Физический смысл этой нормировки состоит в том, чтобы преобразованные данные, т.е. значения региональной составляющей, не отличались бы по масштабу от исходных значений поля, а физический смысл значений 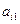заключается в определении весовых коэффициентов для каждого профиля.

5.Нахождение значений первой главной компоненты 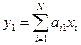т.е.

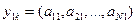
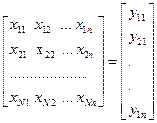
Физический смысл значений первой главной компоненты 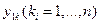состоит в том, что они определяют весовые коэффициенты для каждого пикета исходных данных, аналогично тому, как значения 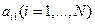определяют весовые коэффициенты для каждого профиля съемки.

6.Оценка региональной составляющей исходного поля характеризующейся наибольшей дисперсией. Эта оценка равна произведению вектора-столбца 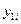на вектор-строку 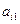с добавлением к каждому элементу образующейся матрицы среднего значения поля по профилю 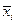, т.е.

=

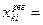
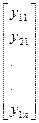
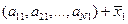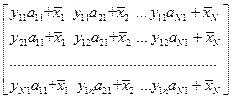
Поскольку значения 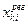представляют оценку региональной составляющей, то разность 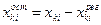оценивает поле локальных составляющих.

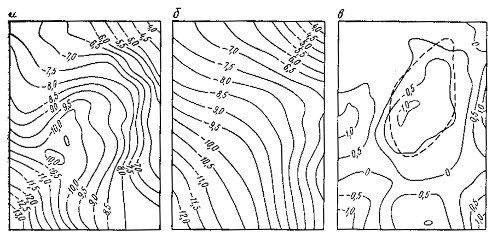
Эффективность метода главных компонент иллюстрируется на рис.3.1(стр.95), на котором приведены исходное поле силы тяжести (а), оценка региональной составляющей (б) и локальная составляющая (в). Пунктиром на рисунке показана область рудного объекта.

Рис.3.1.Исходное поле силы тяжести (а), оценка региональной составляющей (б) и локальной составляющей (в) с использованием метода главных компонент.

Метод главных компонент эффективен при обработке данных на достаточно ограниченных площадях, поскольку не учитывается изменение корреляционных свойств, т.е. структуры корреляционных матриц, по площади.

Следует отметить эффективность применения метода главных компонент при решении задач интерполяции. При этом задача интерполяции физического поля, представленного в виде функции двух переменных x и y, сводится к интерполяции функций, зависящих от одного аргумента. Однако чаще всего метод главных компонент используется при решении задач комплексного анализа данных (см.раздел 9.3).