Линейная регрессия и ее применение.

Линейной регрессией между величинами X и Y называется корреляционная (статистическая) зависимость вида 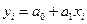(2.6)

Матрица Х в системе (2.5) равна 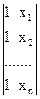соответственно матрица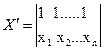

Матрица 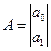, матрица 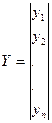. Перемножение матриц 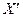и Х дает:

= .

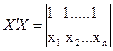
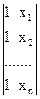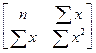Перемножение матриц 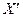и Y равняется = .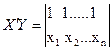

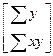Тогда выражение для нахождения коэффициентов 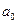и 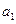в (2.6) принимает вид:

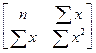
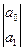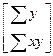= , т.е. система нормальных уравнений будет:

,

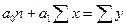
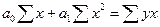отсюда находим:

;

.

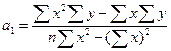Величина 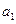определяет угловой коэффициент прямой линии регрессии между X и Y и называется коэффициентом регрессии. Между коэффициентом регрессии 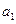и коэффициентом корреляции 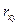имеется связь в виде .

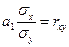Коэффициент корреляции оценивает тесноту линейной связи. Чем больше его величина, тем связь теснее, при 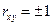связь становится аналитической.

Линейная регрессия широко используется при определении значений одного физического свойства по известным значениям другого. Так, скорость V продольных волн можно определить по плотности горных пород 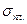. Впервые оценка взаимосвязи скорости и плотности была получена Н.Н.Пузыревым в виде .

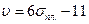Б.М.Уразаевым для эффузивных и метаморфических пород были найдены зависимост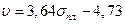и и 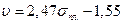. Эти связи обычно меняются в зависимости от возраста пород и района исследований.