Множественная регрессия и ее применение.

Множественная регрессия получается при исследовании связи между несколькими (тремя и более) величинами. Линейная множественная регрессия Y на X₁ и X₂ имеет вид

.

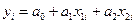Система нормальных уравнений для нахождения коэффициентов 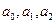в матричной форме (2.5) записывается следующим образом:

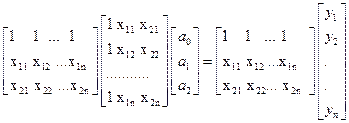
После перемножения матриц получаем:

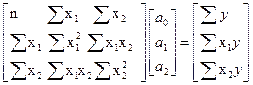
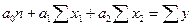
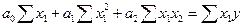
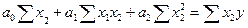
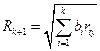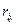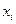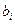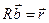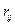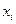Теснота связи оценивается по величине множественного коэффициента корреляции R, которая определяется из выражения , где - коэффициент корреляции величины с y, а значения коэффициентов находятся из решения системы линейных уравнений вида . В этой системе R – корреляционная матрица, составленная из коэффициентов парной корреляции между и 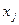. Для линейной регрессии 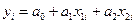матрица 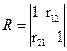. Тогда уравнение 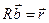примет вид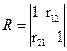 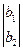= 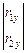, из которого получаем

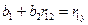
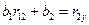
Из последней системы находим коэффициенты

;

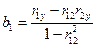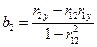
Следовательно, множественный коэффициент корреляции

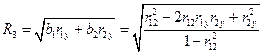
Множественная линейная регрессия успешно используется для определения глубины залегания складчатого фундамента H_i по данным гравиразведки 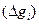и магниторазведки 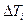в виде: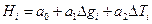

Множественная регрессия широко применяется для построения петрофизических моделей продуктивных залежей углеводородов по данным геофизических исследований скважин. Так, для месторождений Южного Мангышлака использование данных о сопротивлении 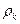по значениям каротажа КС, интенсивности нейтронного гамма каротажа I_НГК и скорости 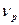по акустическому каротажу приводит к регрессии вида: 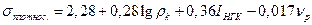при коэффициенте множественной корреляции R=0,75.