ГЛАВА III. Метод главных компонент и его применение

Содержание метода главных компонент.

Метод главных компонент в настоящее время представляет эффективный аппарат комплексного анализа геоданных, и его программное обеспечение является составной частью многих компьютерных технологий по обработке геофизической информации.

Математической моделью метода служит, как и для корреляционно-регрессионного анализа, система случайных величин 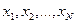. При этом каждая случайная величина обычно содержит n – наблюдений, т.е. исходный массив геоданных представлен матрицей X размерностью :

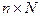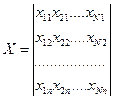
В качестве числа N может быть число профилей съемки, и тогда с помощью главных компонент решается задача оценки регионального тренда (региональной составляющей). Если число N представлено совокупностью различных методов и атрибутов, то путем метода главных компонент решается задача комплексного анализа по разделению исследуемой территории на классы.

Значение n определяет число точек наблюдений по отдельным профилям съемки. Суть метода главных компонент состоит в переходе от системы случайных величин 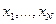к новой системе случайных величин 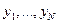, ориентируясь на поведение дисперсий 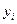. При этом главная компонента определяется как линейная комбинация исходных случайных величин ,

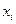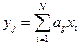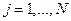; (3.1),

причем первая главная компонента :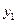

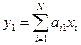(3.2)

обладает максимальной дисперсией среди всех возможных линейных комбинаций вида (3.1).

Величины 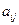являются коэффициентами перехода от одной системы случайных величин 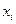к другой системе случайных величин 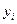. Дисперсии линейных комбинаций 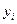располагаются в убывающем порядке, т.е. .

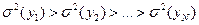Переход от системы величин 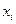к системе 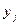сопровождается нормировкой коэффициентов 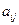в виде 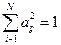. Математически метод главных компонент сводится либо к вычислению ковариационной матрицы В системы случайных величин 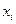, если все 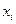измерены в одних и тех же единицах, либо к вычислению корреляционной матрицы R, если случайные величины 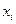измерены в разных физических единицах.

Первый случай соответствует измерениям одного и того же поля по N-профилям съемки, второй случай соответствует измерениям N-разных полей и (или) их атрибутов.

Далее для матрицы В или матрицы R находятся их собственные значения 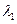и соответствующие этим собственным значениям собственные векторы, которыми являются коэффициенты перехода .

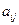Обычно ограничиваются вычислением первых двух-трех главных компонент, поскольку в этих компонентах сосредоточена основная энергия исходных данных. Так, первая главная компонента содержит 70-90% всей энергии (дисперсии) поля или дисперсий совокупности атрибутов при комплексном их анализе.

Физическое истолкование главных компонент является весьма неоднозначным. Однако первая главная компонента практически всегда имеет однозначное истолкование, поскольку ее дисперсия отражает основную энергию поля при обработке данных по площади или энергию нескольких полей и (или) их атрибутов при комплексном анализе данных.

Ниже рассматриваются алгоритмы метода главных компонент при решении задач комплексного анализа геоданных и оценки региональной составляющей одного поля.