Взаимно корреляционная функция и ее применение.
Взаимно корреляционная функция (ВКФ) представляет собой оценку корреляционных свойств между двумя случайными процессами 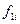 и
и 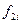 , представленными наблюдениями поля на двух профилях, на двух трассах и т.д.
, представленными наблюдениями поля на двух профилях, на двух трассах и т.д.
Рассчитывается ВКФ по формуле:
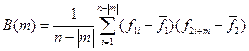 (4.7)
(4.7)
где n - число точек в каждой реализации, т.е. по каждому профилю, трассе и т.д.
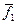 и
и 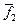 - средние значения наблюденных данных по этим профилям, трассам.
- средние значения наблюденных данных по этим профилям, трассам.
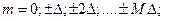 .
.
При равенстве средних значений нулю: 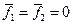 формула (4.7) упрощается
формула (4.7) упрощается
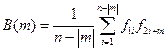 (4.8)
(4.8)
При m=0 значение ВКФ равно произведению значений поля для одноименных дискретов наблюдений по профилям, трассам и т.д.
При 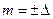 значение ВКФ равно произведению значений поля, смещенных на один дискрет. При этом будем полагать, что смещение на один дискрет влево последующего профиля, т.е.
значение ВКФ равно произведению значений поля, смещенных на один дискрет. При этом будем полагать, что смещение на один дискрет влево последующего профиля, т.е. 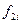 , относительно предыдущего, т.е.
, относительно предыдущего, т.е. 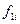 , соответствует положительному смещению, т.е.
, соответствует положительному смещению, т.е. 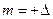 , а смещение вправо соответствует величине
, а смещение вправо соответствует величине 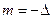 .
.
Поскольку при 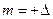 и при
и при 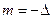 перемножаются разные значения поля, в отличие от расчета АКФ, то ВКФ не является четной функцией, т.е.
перемножаются разные значения поля, в отличие от расчета АКФ, то ВКФ не является четной функцией, т.е. 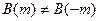 .
.
При 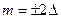 значение ВКФ равно произведению значений поля, смещенных уже на два дискрета и т.д.
значение ВКФ равно произведению значений поля, смещенных уже на два дискрета и т.д.
На практике часто используется нормированная ВКФ, определяемая как 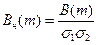 (4.8)
(4.8)
где 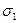 и
и 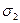 - среднеквадратические отклонения значений поля для первого и второго профиля трассы.
- среднеквадратические отклонения значений поля для первого и второго профиля трассы.
ВКФ нашла применение при решении трех основных задач обработки геофизических данных:
1) Оценка корреляционных свойств сигнала при условии некоррелированности помехи между профилями, трассами и незначительном изменении формы сигнала от профиля к профилю (от трассы к трассе), что обычно выполняется на практике, поскольку расстояние между профилями выбирается таким образом, чтобы сигналы коррелировались между профилями, а помехи, наоборот, были бы некоррелированы. В сейсморазведке расстояния между сейсмоприемниками выбираются таким образом, чтобы нерегулярные волны-помехи были бы некоррелированы между соседними трассами. При этом ВКФ будет равна
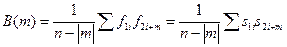 (4.9)
(4.9)
т.е. при совпадении формы сигналов последняя сумма будет равна АКФ сигнала.
Следовательно, ВКФ более надежно оценивает корреляционные свойства сигнала по сравнению с АКФ.
2) Оценка простирания сигналов по положительным экстремумам ВКФ. Положительные экстремумы ВКФ указывают на наличие корреляции сигнала между профилями, трассами, поскольку значение аргумента 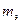 , при котором достигается экстремум ВКФ, соответствует смещению сигнала на последующем профиле относительно его положения на предыдущем. Таким образом, по величине положительных экстремумов ВКФ
, при котором достигается экстремум ВКФ, соответствует смещению сигнала на последующем профиле относительно его положения на предыдущем. Таким образом, по величине положительных экстремумов ВКФ 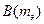 определяется смещение
определяется смещение 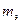 сигнала от профиля к профилю, что и приводит к оценке простирания сигнала.
сигнала от профиля к профилю, что и приводит к оценке простирания сигнала.
В случае сигналов (аномалий) различного простирания ВКФ имеет два или более положительных экстремумов.
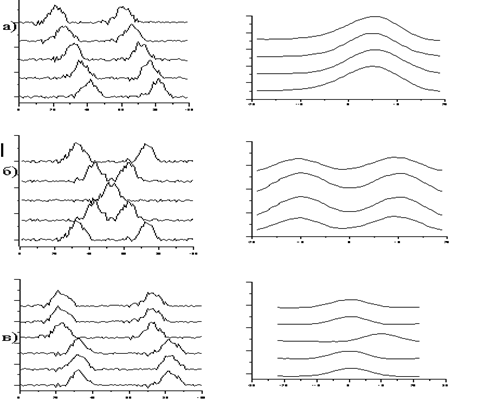
|
| Рис.4.2. Оценка простирания аномалий по экстремальным значениям ВКФ(m) в случае аномалий одного простирания (а), различного простирания (б), смещения аномалий (в). |
На рис.4.2,а приведены результаты наблюдений физического поля по пяти профилям и соответствующие этим наблюдениям графики ВКФ, по которым определяется простирание сигналов, соответствующее их смещению на два дискрета от профиля к профилю.
В случае интерференции двух сигналов, как это изображено на рис.4.2,б, фиксируются два положительных экстремума при 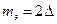 и
и 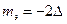 , что в дальнейшем при суммировании данных по нескольким профилям в направлении простирания сигналов позволяет четко провести их разделение по площади съемки.
, что в дальнейшем при суммировании данных по нескольким профилям в направлении простирания сигналов позволяет четко провести их разделение по площади съемки.
Наконец, резкое смещение экстремумов ВКФ для какой-либо пары профилей по сравнению с экстремумами соседних пар профилей позволяет использовать ВКФ для выделения нарушений в распределении поля, как это показано на рис.4.2,в. По такому смещению экстремумов ВКФ обычно картируются разломы с простиранием, близким к простиранию профилей геофизической съемки.
При обработке сейсмических записей построение ВКФ между данными соседних трасс обеспечивает оценку суммарной статической и кинематической поправок, определяемую абсциссой положительного экстремума ВКФ. При знании кинематики, т.е. скоростной характеристики временного разреза, нетрудно определить величину статической поправки.
3) Оценка величины энергетического отношения сигнал/помеха 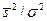 , где
, где 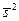 - дисперсия сигнала,
- дисперсия сигнала, 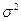 - дисперсия помехи, по значению положительного экстремума ВКФ. При этом величина энергетического отношения сигнал/помеха оценивается без привлечения априорных сведений о сигнале и помехе по формуле А.К.Яновского:
- дисперсия помехи, по значению положительного экстремума ВКФ. При этом величина энергетического отношения сигнал/помеха оценивается без привлечения априорных сведений о сигнале и помехе по формуле А.К.Яновского:
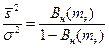 (4.10)
(4.10)
где 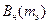 - значение положительного экстремума нормированной ВКФ.
- значение положительного экстремума нормированной ВКФ.
Выражение (4.10) справедливо при двух предположениях: помеха некоррелирована между профилями, а сигнал коррелируется и сохраняет свою форму от профиля к профилю.
Эти предположения приводят к тому, что формула (4.9) оценивает дисперсию сигнала, т.е. 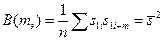 . В то же время АКФ при m=0 равняется сумме дисперсий сигнала и помехи, т.е.
. В то же время АКФ при m=0 равняется сумме дисперсий сигнала и помехи, т.е. 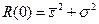 , тогда отношение
, тогда отношение
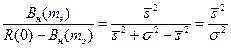 .
.
Дата добавления: 2016-01-16; просмотров: 3064;
