Спектры дискретно заданного сигнала.
Построение спектров дискретно заданного сигнала основано на теореме о том, что любую непрерывную периодическую функцию, удовлетворяющую условиям Дирихле (функция ограничена и имеет конечное число разрывов, т.е. любые геофизические данные удовлетворяют этим условиям) можно представить в виде конечного ряда Фурье:
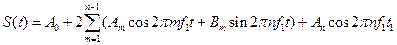(5.1)
содержащего n-констант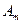 
и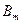 
, называемых коэффициентами Фурье и определяемых таким образом, чтобы значения непрерывного 
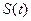и дискретного 
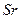сигналов совпадали бы в точках 
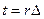, т.е. 
.
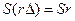Заменяя t на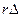 
в (5.1) получаем
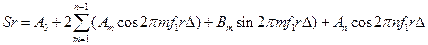(5.2)
В выражении (5.2) абсцисса сигнала r принимает значения r=-n,-n+1,...,-1,0,1,…,n-1.
Таким образом, общее число дискретных значений сигнала N=2n. Начало отсчета по абсциссе расположено в центре сигнала, при этом число положительных, включая r=0, значений абсцисс равно числу отрицательных значений абсцисс. Такая нумерация абсцисс сигнала облегчает расчеты его спектров, хотя выбор начала отсчета не является принципиальным и его можно располагать либо в начале сигнала, либо в его конце.
Значение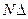 
( 
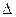- шаг дискретности) определяет период сигнала, а величина 
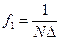- основную частоту сигнала.
При 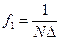синусы и косинусы образуют ортогональную систему. Если левую и правую части выражения (5.2) умножить сначала на 
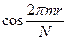, а затем на 
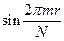и провести суммирование по r, то с учетом ортогональности синусов и косинусов получим явные выражения для коэффициентов Фурье
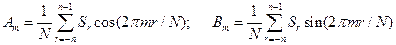(5.3)
где m=1,2,……, номера гармоник.
При m=0, B0=0, а А0 равно среднему значению сигнала; 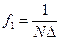- основная частота, 
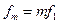- называются гармониками основной частоты.
Номер последней гармоники определяется на основе теоремы Котельникова, согласно которой непрерывный периодический сигнал однозначно описывается дискретным рядом значений, если в последнем отсутствуют частоты выше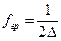 
.
Тогда отношение граничной частоты к основной позволяет найти номер последней гармоники, т.е.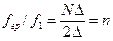 
.
Граничная частота называется частотой Найквиста. По коэффициентам Фурье (5.3) рассчитываются спектры дискретно заданного сигнала:
-амплитудный спектр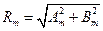 
(5.4)
-фазовый спектр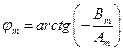 
(5.5)
Амплитудный спектр описывает распределение амплитуд по различным гармоникам, спектр – дискретный или линейчатый. Фазовый спектр характеризует распределение фаз по разным гармоникам.
Фаза представляет отклонение начальной точки гармоники от центра отсчета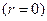 
и в отличие от положительных величин амплитудного спектра, принимает как положительные, так и отрицательные значения. Оба спектра рассчитываются обычно для значений 
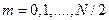, где N – число значений сигнала. Ввиду периодичности сигнала, заложенной основами анализа Фурье, эти спектры также являются периодическими.
По амплитудному и фазовому спектрам можно получить выражение для комплексного спектра:
-комплексный спектр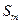 
представляет комплексное число и может быть записан в разных вариантах:
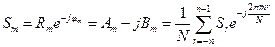(5.6)
.
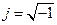Известно, что для комплексного числа имеется комплексно-сопряженное, определяющее
-комплексно-сопряженный спектр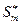 
:
= 
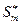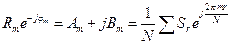(5.7)
Комплексно-сопряженный спектр представляет зеркальное отображение комплексного спектра в область отрицательных гармоник.
Кроме перечисленных видов спектров часто используется энергетический спектр;
-энергетический спектр есть произведение комплексного спектра на комплексно-сопряженный или квадрат амплитудного спектра, т.е.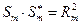 
.
По энергетическому спектру рассчитывается дисперсия сигнала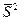 
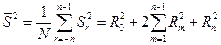(5.8)
Вычисление спектров представляет прямое преобразование Фурье.
Вычисление значений сигнала по его спектрам представляет обратное преобразование Фурье, которое для дискретно заданного сигнала может быть выражено, как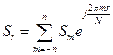 
.
На практике используется тригонометрическая форма обратного преобразования Фурье дискретно заданного сигнала
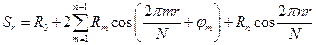(5.9)
где 
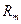и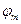 
- значения амплитудного и фазового спектров.
Рассмотрим пример вычисления амплитудного спектра сигнала, заданного следующими его значениями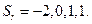 
.
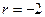
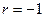
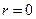
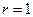Среднее значение сигнала равно нулю, т.е.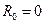 
. Поскольку N=4, то достаточно рассчитать две гармоники.
Коэффициенты 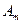и 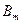равны соответственно:
;
;
;
.
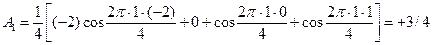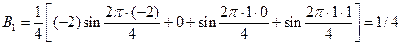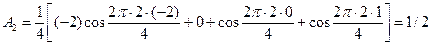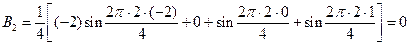Отсюда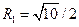 
; 
.
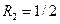Рассмотрим пример вычисления значения сигнала в точке 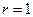при заданных его амплитудном и фазовом спектрах в таблице.
| m | Rm |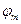
|
| -300 |
С этой целью используем выражение (5.9), где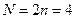 
.
.
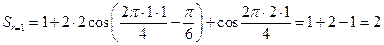Дата добавления: 2016-01-16; просмотров: 2513;