Глава II. Дискретность электронных и атомных состояний. 1 страница
Эффект Комптона.
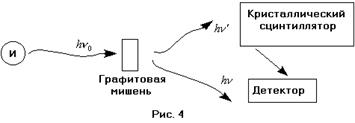 В 1922 – 23 гг. Комптоном был исследован характер взаимодействия фотона и электрона. В результате поставленных опытов был сделан вывод, что при определённых условиях они имеют характер механического столкновения. Рассмотрим схему опыта, натолкнувшего Комптона на такую мысль. В опыте, в качестве источника излучения, использовалась рентгеновская трубка с молибденовым анодом. Фотон попадал на графитовую мишень из источника рентгеновского излучения1. После рассеяния на мишени, исследовался спектр рассеянного излучения с помощью кристаллического сцинтиллятора. Вторичное излучение, полученное с помощью сцинтиллятора, попадало на фотодетектор.
В 1922 – 23 гг. Комптоном был исследован характер взаимодействия фотона и электрона. В результате поставленных опытов был сделан вывод, что при определённых условиях они имеют характер механического столкновения. Рассмотрим схему опыта, натолкнувшего Комптона на такую мысль. В опыте, в качестве источника излучения, использовалась рентгеновская трубка с молибденовым анодом. Фотон попадал на графитовую мишень из источника рентгеновского излучения1. После рассеяния на мишени, исследовался спектр рассеянного излучения с помощью кристаллического сцинтиллятора. Вторичное излучение, полученное с помощью сцинтиллятора, попадало на фотодетектор.
 |
Исследуя спектр, Комптон заметил, что лучи, рассеянные на угол меньше
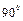 , обладают большей длиной волны, чем исходное излучение, так что частота
, обладают большей длиной волны, чем исходное излучение, так что частота 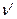 вторичной волны оказывается вопреки классической теории меньше, чем частота
вторичной волны оказывается вопреки классической теории меньше, чем частота 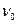 первоначального электромагнитного поля. Причём, энергия рассеянных фотонов (а значит и их частота) зависит от угла рассеяния
первоначального электромагнитного поля. Причём, энергия рассеянных фотонов (а значит и их частота) зависит от угла рассеяния 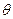 . С позиции волновой теории это явление необъяснимо. На основании опытных данных, исследуя зависимость мощности рассеянного излучения от длины его волны при различных углах рассеяния, Комптон сделал вывод, что сдвиг длины волны
. С позиции волновой теории это явление необъяснимо. На основании опытных данных, исследуя зависимость мощности рассеянного излучения от длины его волны при различных углах рассеяния, Комптон сделал вывод, что сдвиг длины волны 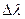 линейно пропорционален
линейно пропорционален 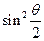 , где
, где 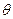 – угол рассеяния. Таким образом, чтобы поставить знак равенства, необходимо умножить
– угол рассеяния. Таким образом, чтобы поставить знак равенства, необходимо умножить 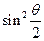 на некоторую константу. Мы можем записать:
на некоторую константу. Мы можем записать: 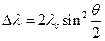 (1), где
(1), где 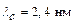 – комптоновская постоянная (комптоновская длина волны). Рассмотрим теперь графики зависимости
– комптоновская постоянная (комптоновская длина волны). Рассмотрим теперь графики зависимости 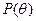 для различных
для различных 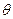 .
.
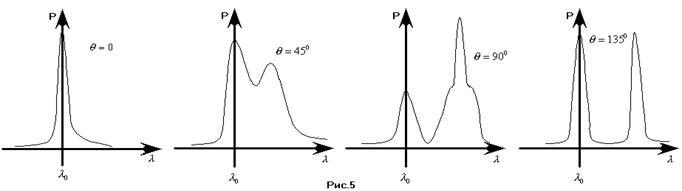
Из графиков (см. рис 5) видно, что функция 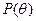 при различных
при различных 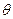 имеет максимум не только при исходной длине волны, но и при некоторых других.
имеет максимум не только при исходной длине волны, но и при некоторых других.
Для объяснения эффекта Комптона, Дебай рассмотрел упругое столкновение двух частиц: светового кванта и электрона. Надо сказать, что электрон, с которым происходит упругое столкновение, является свободным электроном, т. е. электроном проводимости.
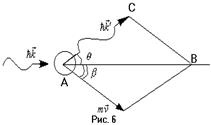 Пусть до взаимодействия электрон неподвижен. Фотон с импульсом
Пусть до взаимодействия электрон неподвижен. Фотон с импульсом 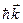 взаимодействует с электроном мишени, рассеивается на нём. Импульс фотона изменяется и становится равным
взаимодействует с электроном мишени, рассеивается на нём. Импульс фотона изменяется и становится равным 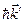 . Электрон также рассеивается и при этом получает импульс
. Электрон также рассеивается и при этом получает импульс 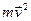 . Таким образом, мы можем записать законы сохранения импульса и энергии:
. Таким образом, мы можем записать законы сохранения импульса и энергии:
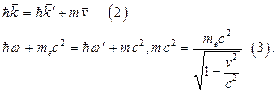
В формуле (3) под 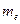 подразумевается масса покоя электрона. Проведём некоторые преобразования. Сложим импульс по правилу параллелограмма. Для треугольника
подразумевается масса покоя электрона. Проведём некоторые преобразования. Сложим импульс по правилу параллелограмма. Для треугольника 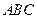 применим теорему косинусов:
применим теорему косинусов:
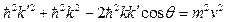 . Так как
. Так как 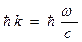 , то
, то
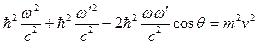 (4).
(4).
Из равенства (3) следует, что 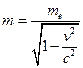 или
или 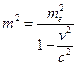 . Из последнего выражения найдём
. Из последнего выражения найдём 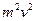 :
: 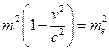
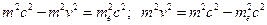 . Подставим последнее выражение в формулу (4), и, учитывая закон сохранения энергии:
. Подставим последнее выражение в формулу (4), и, учитывая закон сохранения энергии: 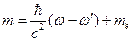 (получается из формулы (3)), запишем:
(получается из формулы (3)), запишем:
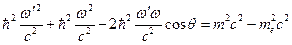
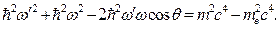
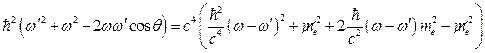

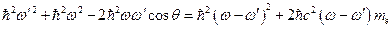
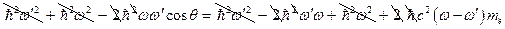
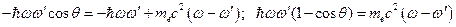 . Разделим последнее выражение на
. Разделим последнее выражение на 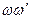 :
: 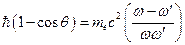 ;
; 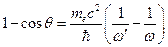 . Так как
. Так как 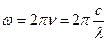 , то
, то 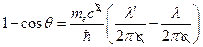 . Преобразуя последнее выражение, получим:
. Преобразуя последнее выражение, получим: 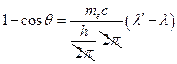 . Обозначим
. Обозначим 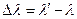 . Тогда
. Тогда 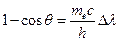 . Отсюда
. Отсюда 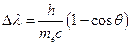 или
или 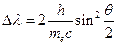 (5). В последней формуле выражение
(5). В последней формуле выражение 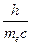 является постоянной, так как из таковых состоит. Вычисления показывают, что
является постоянной, так как из таковых состоит. Вычисления показывают, что 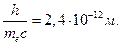 , что в точности совпадает с комптоновской постоянной. Таким образом, (5) можно переписать так
, что в точности совпадает с комптоновской постоянной. Таким образом, (5) можно переписать так 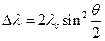 , что в точности совпадает с опытной формулой (1). Из полученного соотношения следует, что квантовая теория хорошо объясняет эффект Комптона, исходя из корпускулярных свойств излучения. То есть столкновение электрона с фотоном рассматривается как столкновение двух упругих шариков. Данная механическая модель очень хорошо аппроксимирует истинное положение дел и в рамках данного эффекта ею очень удобно пользоваться.
, что в точности совпадает с опытной формулой (1). Из полученного соотношения следует, что квантовая теория хорошо объясняет эффект Комптона, исходя из корпускулярных свойств излучения. То есть столкновение электрона с фотоном рассматривается как столкновение двух упругих шариков. Данная механическая модель очень хорошо аппроксимирует истинное положение дел и в рамках данного эффекта ею очень удобно пользоваться.
Как было сказано выше, Дебай построил свою теорию на рассеянных электронах. Тем не менее, существуют эффекты наподобие комптоновского, которые очень трудно зарегистрировать. Например, рассеяние на протоне. Так как 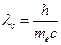 , то при увеличении массы частицы фотон будет приобретать всё меньшее изменение импульса. Так для протона
, то при увеличении массы частицы фотон будет приобретать всё меньшее изменение импульса. Так для протона 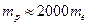 , поэтому и изменение длины волны фотона при рассеянии на протоне будет в 2000 раз меньшим. Из вышесказанного следует, что наличие в комптоновском эффекте не смещённой длины волны есть следствие рассеяния фотонов на атомах – когерентное рассеяние. Очевидно, что масса атома гораздо больше массы электрона, поэтому
, поэтому и изменение длины волны фотона при рассеянии на протоне будет в 2000 раз меньшим. Из вышесказанного следует, что наличие в комптоновском эффекте не смещённой длины волны есть следствие рассеяния фотонов на атомах – когерентное рассеяние. Очевидно, что масса атома гораздо больше массы электрона, поэтому 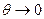 .
.
Другое подтверждение корпускулярной теории должно было дать следующее предположение. Если свет состоит из потока частиц, мы могли бы выделить частицу. В настоящее время существуют установки, позволяющие регистрировать до 5 – 6 фотонов. В начале же века, чтобы построить подобный опыт, соответствующей техники не было. Тем не менее, С. И. Вавилов поставил эксперимент по исследованию флуктуаций интенсивности светового потока, а значит и числа фотонов. Дискретность светового потока имеет место быть не только во времени, но и в пространстве. В качестве приёмника Вавилов использовал свой глаз, так как человеческий глаз обладает высокой светочувствительностью. Его разрешающая способность составляет примерно 10 – 20 фотонов. Схема опыта, поставленного Вавиловым, такова. Брался источник белого света и пропускал луч через аттенюатор – диск с вырезанным сегментом, насажанный на ось и способный вращаться. Скорость вращения аттенюатора выставлялась равной 1 об/с. Потом свет падал на зелёный светофильтр, а после него – на собирающую линзу и управляемый аттенюатор, изменяющий интенсивность света. После всего луч попадал в глаз к наблюдателю.
Хронограф, соединённый с первым аттенюатором, ставил отметки каждый раз, когда через аттенюатор проходил луч. Второй хронограф приводился в действие самим наблюдателем. Опыт показал, что для большой интенсивности света отметки независимого хронографа и хронографа испытателя совпадали. При уменьшении интенсивности до некоторой величины, испытатель переставал регистрировать некоторые вспышки. Статистическая обработка данных показала, что в данном случае имеет место статистические флуктуации числа фотонов в каждой отдельной вспышке светового потока. Точно таким же образом исследовались 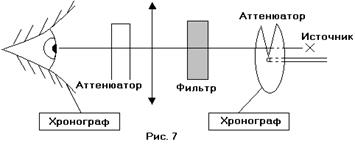 флуктуации когерентных лучей. Когерентные лучи получались методом Юнга. Опыт показал, что флуктуации фотонов в каждом из двух когерентных лучей независимы. Исследуя этим же методом флуктуации фотонов в двух поляризованных лучах[1], полученных с помощью призмы Волластона[2], получили, что они также независимы.
флуктуации когерентных лучей. Когерентные лучи получались методом Юнга. Опыт показал, что флуктуации фотонов в каждом из двух когерентных лучей независимы. Исследуя этим же методом флуктуации фотонов в двух поляризованных лучах[1], полученных с помощью призмы Волластона[2], получили, что они также независимы.
§ 1.3.Интерференция фотонов.
Из курса электричества известно, что к электромагнитной волне может быть применено скалярное волновое уравнение: 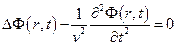 (1), где
(1), где 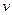 – скорость распространения волны, а
– скорость распространения волны, а 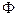 – одно из следующих полей:
– одно из следующих полей: 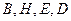 . Уравнению (1) удовлетворяют плоские электромагнитные волны, то есть волны, которые описываются следующим уравнением:
. Уравнению (1) удовлетворяют плоские электромагнитные волны, то есть волны, которые описываются следующим уравнением: 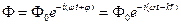 , где
, где 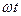 – временная фаза, а
– временная фаза, а 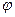 – пространственная фаза. Если эту функцию подставить в (1), волновое уравнение примет вид:
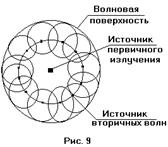
– пространственная фаза. Если эту функцию подставить в (1), волновое уравнение примет вид: 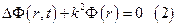 . Уравнение (2) называют уравнением Гельмгольца. Оно описывает пространственные характеристики гармонической волны в однородной среде. На этом уравнении базируется теория интерференции и дифракции. Рассмотрим классический опыт Юнга по интерференции от двух щелей. Сферическая волна из источника
. Уравнение (2) называют уравнением Гельмгольца. Оно описывает пространственные характеристики гармонической волны в однородной среде. На этом уравнении базируется теория интерференции и дифракции. Рассмотрим классический опыт Юнга по интерференции от двух щелей. Сферическая волна из источника 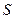 падает на непрозрачный экран с одной щелью. Щель является источником вторичной сферической волны, интенсивность которой уже много меньше исходной. Полученная волна распространяется и падает, в свою очередь, на непрозрачный экран с двумя отверстиями, которые являются теперь источниками вторичных волн. Так как отверстия два, то и полученных волн тоже будет две. Данные волны обладают свойством когерентности, поэтому для них возможно явление интерференции.
падает на непрозрачный экран с одной щелью. Щель является источником вторичной сферической волны, интенсивность которой уже много меньше исходной. Полученная волна распространяется и падает, в свою очередь, на непрозрачный экран с двумя отверстиями, которые являются теперь источниками вторичных волн. Так как отверстия два, то и полученных волн тоже будет две. Данные волны обладают свойством когерентности, поэтому для них возможно явление интерференции. 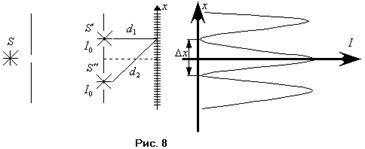 Основное противоречие здесь заключается в следующем: явление фотоэффекта и эффекта Комптона, казалось бы, довольно убедительно показали, что свет есть ничто иное, как поток корпускул. Тогда, так как интенсивность зависит от числа фотонов, то если освещать непрозрачный экран двумя лучами, по идее, интенсивность для каждой точки экрана должна быть выше, чем если бы его освещали только из одного источника. На деле же для некоторых участков экрана интенсивность, в соответствии с рис. 8, получается более низкой, а для других – более высокой, чем должна бы в соответствии с квантовой моделью. С точки зрения корпускулярной теории это явление объяснить нельзя. Однако, если ввести в рассмотрение волновую модель света, описанное явление получает замечательное объяснение с помощью явления интерференции. Таким образом, для света характерны корпускулярные и волновые свойства.
Основное противоречие здесь заключается в следующем: явление фотоэффекта и эффекта Комптона, казалось бы, довольно убедительно показали, что свет есть ничто иное, как поток корпускул. Тогда, так как интенсивность зависит от числа фотонов, то если освещать непрозрачный экран двумя лучами, по идее, интенсивность для каждой точки экрана должна быть выше, чем если бы его освещали только из одного источника. На деле же для некоторых участков экрана интенсивность, в соответствии с рис. 8, получается более низкой, а для других – более высокой, чем должна бы в соответствии с квантовой моделью. С точки зрения корпускулярной теории это явление объяснить нельзя. Однако, если ввести в рассмотрение волновую модель света, описанное явление получает замечательное объяснение с помощью явления интерференции. Таким образом, для света характерны корпускулярные и волновые свойства.
Опыт показывает, что картинка распределения интенсивности 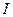 результата интерференции в зависимости от координаты
результата интерференции в зависимости от координаты 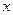 имеет вид указанный на рис. 8 вид. Формально, характеризуя зависимость
имеет вид указанный на рис. 8 вид. Формально, характеризуя зависимость 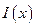 , мы можем записать:
, мы можем записать: 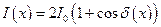 (3). Здесь
(3). Здесь 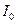 – интенсивность источников
– интенсивность источников 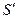 и
и 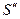 . Множитель 2 возникает вследствие того, что у нас два источника. В последней формуле
. Множитель 2 возникает вследствие того, что у нас два источника. В последней формуле 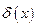 является разностью фаз между интерферирующими лучами в точке наблюдения. Найдём её. Запишем уравнения плоской волны для источников
является разностью фаз между интерферирующими лучами в точке наблюдения. Найдём её. Запишем уравнения плоской волны для источников 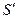 и
и 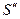 :
: 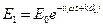 и
и 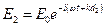 . Тогда
. Тогда 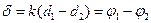 . Отсюда для корпускулярной интерпретации опыта Юнга возникают чрезвычайно большие трудности. Если каким-то образом приписать отдельному фотону фазу, тогда необходимо считать, что
. Отсюда для корпускулярной интерпретации опыта Юнга возникают чрезвычайно большие трудности. Если каким-то образом приписать отдельному фотону фазу, тогда необходимо считать, что 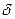 в (3) является разностью фаз двух фотонов, прошедших через различные щели. Но это противоречит закону сохранения энергии, поскольку два фотона при попадании в одну точку экрана выделяют энергию, не равную сумме их энергий. При некоторых условиях
в (3) является разностью фаз двух фотонов, прошедших через различные щели. Но это противоречит закону сохранения энергии, поскольку два фотона при попадании в одну точку экрана выделяют энергию, не равную сумме их энергий. При некоторых условиях 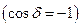 они могут взаимно уничтожить друг друга, при других
они могут взаимно уничтожить друг друга, при других 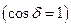 – выделенная энергия в два раза больше, чем сумма энергий фотонов. Ясно, что такая интерпретация фазы неприемлема. Поэтому не представляется возможным приписать фотону характеристику, аналогичную фазе электромагнитной волны. Характеристика, аналогичная фазе волны, принадлежит не фотону, а состоянию, которое описывает его движение. Это значит, что интерференцию необходимо описать как явление, происходящее при наличии лишь одного фотона. Эксперименты с очень маленькими интенсивностями света, когда можно быть уверенным, что одновременно в образовании интерференционной картины участвует не более одного фотона, показали, что интерференционная картина образуется попаданием на экран отдельных фотонов. Это говорит о том, что движение отдельного фотона в интерференционных не зависит от наличия других. Фотон интерферирует сам собой. Вследствие этого говорят, что существует вероятность наблюдения фотона в тот или иной момент времени в той или иной точке пространства. Поэтому функция
– выделенная энергия в два раза больше, чем сумма энергий фотонов. Ясно, что такая интерпретация фазы неприемлема. Поэтому не представляется возможным приписать фотону характеристику, аналогичную фазе электромагнитной волны. Характеристика, аналогичная фазе волны, принадлежит не фотону, а состоянию, которое описывает его движение. Это значит, что интерференцию необходимо описать как явление, происходящее при наличии лишь одного фотона. Эксперименты с очень маленькими интенсивностями света, когда можно быть уверенным, что одновременно в образовании интерференционной картины участвует не более одного фотона, показали, что интерференционная картина образуется попаданием на экран отдельных фотонов. Это говорит о том, что движение отдельного фотона в интерференционных не зависит от наличия других. Фотон интерферирует сам собой. Вследствие этого говорят, что существует вероятность наблюдения фотона в тот или иной момент времени в той или иной точке пространства. Поэтому функция 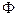 из уравнения (2), описывающего распространение отдельного фотона, будет иметь смысл не, например, напряжённости электрического поля
из уравнения (2), описывающего распространение отдельного фотона, будет иметь смысл не, например, напряжённости электрического поля 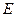 в данной точке пространства, а плотности вероятности нахождения фотона в данной точке пространства в данный момент времени
в данной точке пространства, а плотности вероятности нахождения фотона в данной точке пространства в данный момент времени 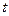 . Таким образом, корпускулярное описание не позволяет говорить о движении фотона по какой-то траектории. Не имеет также смысла говорить, что фотон прошёл при интерференции через ту или иную щель.
. Таким образом, корпускулярное описание не позволяет говорить о движении фотона по какой-то траектории. Не имеет также смысла говорить, что фотон прошёл при интерференции через ту или иную щель.
§ 1.4. Дифракция рентгеновских лучей в кристаллах.
Вообще говоря, дифракцией называют огибание волной препятствий, не связанное с явлениями отражения, преломления или рассеяния света. Строго говоря, дифракция является результатом интерференции вторичных волн. Основой для описания дифракции служит принцип Гюйгенса – Френеля, заключающийся в том, что все точки поверхности волнового фронта являются источниками вторичных волн, а результирующее волновое поле является суперпозицией волн, исходящих из вторичных источников. Таким образом, чтобы узнать, какова будет интенсивность в произвольной точке экрана, необходимо знать результат интерференции вторичных волн в этой точке. По идее, при дифракции на двух щелях (см. рис. 8) напротив непрозрачной части экрана должно наблюдаться тёмное пятно. Однако можно сделать так, чтобы в этой точке было пятно светлое. Это – следствие явления интерференции вторичных волн.
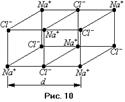
 Дифракция волны на препятствии происходит всегда, независимо от размеров самого препятствия или длины волны. Другое дело, наблюдать дифракцию. Когда размеры препятствия гораздо больше длины волны, дифракцию можно обнаружить на значительном удалении от препятствия. Если же длина волны соизмерима с размерами препятствия, то дифракцию можно наблюдать в непосредственной близости от препятствия. Длина волны рентгеновского излучения составляет 1 – 0,001 нм. Поэтому, для удобства изучения рассматривают дифракцию рентгеновского излучения на кристаллах. Кристаллами называется упорядоченная структура, в узлах которой находятся молекулы, атомы, ионы или электроны. Такая структура называется кристаллической решёткой. Наиболее простой вид имеет кубическая кристаллическая решётка. Решёткой такого вида обладают графит, поваренная соль и т. д. Рассмотрим её строение на примере кристаллов поваренной соли. В узлах данной решётки сосредоточены ионы хлора и натрия. Линиями показаны химические связи, существующие в кристалле. Параметр
Дифракция волны на препятствии происходит всегда, независимо от размеров самого препятствия или длины волны. Другое дело, наблюдать дифракцию. Когда размеры препятствия гораздо больше длины волны, дифракцию можно обнаружить на значительном удалении от препятствия. Если же длина волны соизмерима с размерами препятствия, то дифракцию можно наблюдать в непосредственной близости от препятствия. Длина волны рентгеновского излучения составляет 1 – 0,001 нм. Поэтому, для удобства изучения рассматривают дифракцию рентгеновского излучения на кристаллах. Кристаллами называется упорядоченная структура, в узлах которой находятся молекулы, атомы, ионы или электроны. Такая структура называется кристаллической решёткой. Наиболее простой вид имеет кубическая кристаллическая решётка. Решёткой такого вида обладают графит, поваренная соль и т. д. Рассмотрим её строение на примере кристаллов поваренной соли. В узлах данной решётки сосредоточены ионы хлора и натрия. Линиями показаны химические связи, существующие в кристалле. Параметр 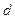 определяет расстояние, начиная с которого строение решётки повторяется.
определяет расстояние, начиная с которого строение решётки повторяется. 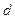 называют периодом кристаллической решётки. Существуют более сложные кристаллические решётки, например, кубическая гранецентрическая кристаллическая решётка, объёмоцентрическая решётка и т. д. Как уже говорилось ранее, существует возможность использовать кристаллическую решётку в качестве дифракционной. Однако это будет трёхмерная дифракционная решётка. Рассмотрим процессы, происходящие при прохождении луча сквозь кристалл. Если волна падает на кристалл в определённом направлении, то мы можем рассматривать процесс прохождение волны через кристалл как последовательные отражения её от кристаллических плоскостей. В этом случае ион становится источником вторичных волн. При этом часть луча отражается от ионов первой кристаллической плоскости, а другая часть проходит дальше. Так как угол падения равен углу отражения, то те фотоны, угол падения которых был одинаков, после отражения будут двигаться параллельно друг другу. Чтобы собрать их вместе, поставим на пути отражённого луча собирающую линзу. Тогда на экране, расположенном за линзой мы сможем наблюдать дифракционную картину. Как известно, интерференционный максимум или минимум определяются тем, приходят ли волны в данную точку синфазно или же в противофазе. Разность фаз двух лучей будет зависеть от расстояния, пройденного этими лучами.
называют периодом кристаллической решётки. Существуют более сложные кристаллические решётки, например, кубическая гранецентрическая кристаллическая решётка, объёмоцентрическая решётка и т. д. Как уже говорилось ранее, существует возможность использовать кристаллическую решётку в качестве дифракционной. Однако это будет трёхмерная дифракционная решётка. Рассмотрим процессы, происходящие при прохождении луча сквозь кристалл. Если волна падает на кристалл в определённом направлении, то мы можем рассматривать процесс прохождение волны через кристалл как последовательные отражения её от кристаллических плоскостей. В этом случае ион становится источником вторичных волн. При этом часть луча отражается от ионов первой кристаллической плоскости, а другая часть проходит дальше. Так как угол падения равен углу отражения, то те фотоны, угол падения которых был одинаков, после отражения будут двигаться параллельно друг другу. Чтобы собрать их вместе, поставим на пути отражённого луча собирающую линзу. Тогда на экране, расположенном за линзой мы сможем наблюдать дифракционную картину. Как известно, интерференционный максимум или минимум определяются тем, приходят ли волны в данную точку синфазно или же в противофазе. Разность фаз двух лучей будет зависеть от расстояния, пройденного этими лучами.
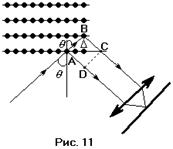
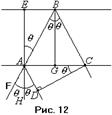 Дадим теперь явлению дифракции на кристалле некоторую количественную оценку. Отражённые лучи, как видно из рис. 11, будут иметь разность хода равную
Дадим теперь явлению дифракции на кристалле некоторую количественную оценку. Отражённые лучи, как видно из рис. 11, будут иметь разность хода равную 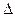 . Пусть лучи падают на кристалл под определённым углом
. Пусть лучи падают на кристалл под определённым углом 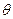 . Потребуем выполнения в точке наблюдения условия максимума интенсивности:
. Потребуем выполнения в точке наблюдения условия максимума интенсивности: 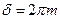 (
( 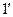 ), где
), где 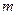 – произвольное целое положительное число. Увеличим часть рис. 11 чтобы рассмотреть его геометрию. Очевидно, что разность хода
– произвольное целое положительное число. Увеличим часть рис. 11 чтобы рассмотреть его геометрию. Очевидно, что разность хода 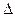 будет определяться следующим соотношением:
будет определяться следующим соотношением: 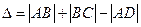 (1). Так как треугольники
(1). Так как треугольники 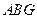 и
и 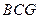 равны1, то сторона
равны1, то сторона 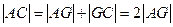 . Найдём её.
. Найдём её. 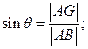
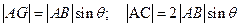 . Нам известно, что
. Нам известно, что 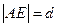 – период кристаллической решётки. Тогда
– период кристаллической решётки. Тогда 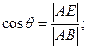
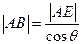 (2). Таким образом,
(2). Таким образом, 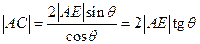 (3). Рассмотрим теперь
(3). Рассмотрим теперь 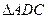 . Угол
. Угол 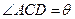 . Этот факт легко доказывается, если записать выражения для всех углов треугольника1. Поэтому
. Этот факт легко доказывается, если записать выражения для всех углов треугольника1. Поэтому 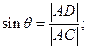
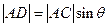 . Таким образом,
. Таким образом, 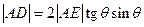 или
или 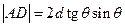 . Так как
. Так как 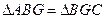 , то
, то 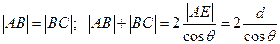 . Возвращаясь к выражению (1), с учётом последнего выражения, а также уравнения (3), мы можем записать:
. Возвращаясь к выражению (1), с учётом последнего выражения, а также уравнения (3), мы можем записать: 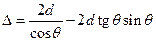 . Преобразуем последнее выражение:
. Преобразуем последнее выражение: 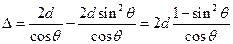 ;
; 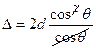 ,
, 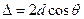 (4). С другой стороны, разность фаз между волнами, отражёнными от соседних поверхностей, равна
(4). С другой стороны, разность фаз между волнами, отражёнными от соседних поверхностей, равна 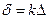 . Так как мы требовали условие интерференционного максимума, то, в соответствии с формулой (
. Так как мы требовали условие интерференционного максимума, то, в соответствии с формулой ( 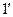 ), мы можем записать:
), мы можем записать: 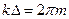 . Учитывая выражение для
. Учитывая выражение для 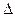 (4), получим:
(4), получим: 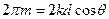 . По определению
. По определению 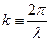 . Подставляя это выражение в последнюю формулу, получим:
. Подставляя это выражение в последнюю формулу, получим: 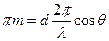 или, окончательно,
или, окончательно, 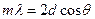 (5). Формула (5) называется
(5). Формула (5) называется 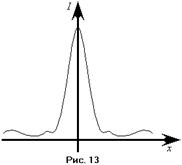 условием Вульфа – Брэгга. Она показывает, под каким углом на кристалл с заданным периодом кристаллической решётки должно падать излучение, чтобы было возможным наблюдение интерференционных максимумов. В тоже время, с помощью формулы (5) мы можем определить период кристаллической решётки исследуемого кристалла. Известно, что в случае объёмной кристаллической решётке, особенно острым будет центральный максимум, т. е.
условием Вульфа – Брэгга. Она показывает, под каким углом на кристалл с заданным периодом кристаллической решётки должно падать излучение, чтобы было возможным наблюдение интерференционных максимумов. В тоже время, с помощью формулы (5) мы можем определить период кристаллической решётки исследуемого кристалла. Известно, что в случае объёмной кристаллической решётке, особенно острым будет центральный максимум, т. е. 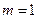 (см. рис. 13). Поэтому, посылая на кристалл лучи под различными углами, мы при каком-то конкретном угле сможем наблюдать максимум. Зная угол, легко определить и период кристаллической решётки. На формуле Вульфа – Брэгга основан метод рентгеноскопического анализа. Методы рентгеноскопического анализа делятся на две группы в зависимости от условий съёмки:
(см. рис. 13). Поэтому, посылая на кристалл лучи под различными углами, мы при каком-то конкретном угле сможем наблюдать максимум. Зная угол, легко определить и период кристаллической решётки. На формуле Вульфа – Брэгга основан метод рентгеноскопического анализа. Методы рентгеноскопического анализа делятся на две группы в зависимости от условий съёмки:
1. Угол падения луча на кристалл постоянен, но изменяется длина падающей волны.
2. Длина волны постоянна, но изменяется угол падения её на кристалл.
К первому типу относится метод Лауэ. Его суть заключается в том, что на кристалл ориентированный под определённым углом по отношению к лучу, падает пучок непрерывного излучения2. Для излучения с некоторой длиной волны выполнится условие Вульфа – Брэгга. По интерференционной картине и геометрии опыта легко вычислить длину этой волны, а значит и период кристаллической решётки.
Второй тип осуществляется двумя методами.
1. Метод вращения (метод Брэгга). Данный метод заключается в том, что монокристалл облучается монохроматическим рентгеновским излучением. При этом кристалл вращается вокруг оси кристаллографической зоны, ортогональной падающему пучку света так, что различные плоскости кристалла становятся последовательно в положение, соответствующее условию Вульфа – Брэгга. Для какого-то угла условие Вульфа – Брэгга будет выполнено. Зная угол, и результат интерференции, можно найти период кристаллической решётки. Так как излучение падает на различные кристаллические плоскости, то мы в случае сложного строения кристалла сможем полностью определить все расстояния между различными его плоскостями. Поэтому метод Брэгга используется, в основном, для анализа сложных кристаллических структур.
2. Метод Дебая – Шерера. В этом методе поликристалл или мелкий порошок из монокристаллических зёрен освещался монохроматическим излучением. Среди множества произвольно ориентированных монокристаллов всегда будут существовать такие, для которых будет выполнено условие Вульфа – Брэгга. Зная интерференционную картину, длину падающей волны и геометрию опыта, можно сделать заключение о строении кристалла.
Таким образом, опыты по дифракции рентгеновского излучения на кристалле позволили убедительно доказать волновую природу данного излучения, а также найти длину его волны.
§ 1.5.Волновые свойства корпускул.
Исследование свойств электромагнитного излучения, в частности рентгеновского, наглядно показали, что его поведение невозможно характеризовать какими-то конкретными рамками, т. е. или волна, или частица. Явление фотоэффекта, эффект Комптона, как мы уже видели, наглядно показывают, что рентгеновское излучение должно являться потоком частиц. В то же время опыты по дифракции рентгеновского излучения на кристаллах говорят в пользу его волновой природы. Таким образом, рентгеновскому излучению присущи как волновые, так и корпускулярные свойства. Данное обстоятельство наталкивает на мысль, что все микрочастицы могут вести себя подобно волнам. Были поставлены опыты, результаты которых это предположение подтвердили.
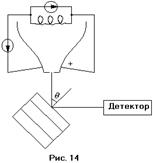 Классическими опытами, в которых были обнаружены волновые свойства частиц, являются опыты Девисона и Джермера (1927 г.). В них наблюдалась дифракция электронов, рассеянных на грани кристалла. Рассмотрим схему данного опыта. Электроны испускались раскалённой нитью, которая служила катодом. Между нитью и анодом подавалась разность дополнительная потенциалов. В аноде делалось отверстие. Электроны пролетали в него и падали на кристаллическую пластинку. Рассеянное излучение регистрировалось детектором. В первом опыте изменялся угол
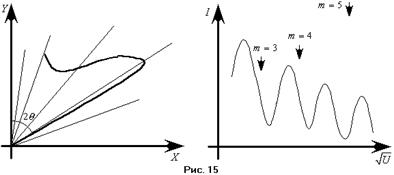
Классическими опытами, в которых были обнаружены волновые свойства частиц, являются опыты Девисона и Джермера (1927 г.). В них наблюдалась дифракция электронов, рассеянных на грани кристалла. Рассмотрим схему данного опыта. Электроны испускались раскалённой нитью, которая служила катодом. Между нитью и анодом подавалась разность дополнительная потенциалов. В аноде делалось отверстие. Электроны пролетали в него и падали на кристаллическую пластинку. Рассеянное излучение регистрировалось детектором. В первом опыте изменялся угол 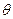 падения электронов на пластинку. Результат рассеяния отмечался на полярной диаграмме (см. рис. 15). Максимум интенсивности приходился на угол
падения электронов на пластинку. Результат рассеяния отмечался на полярной диаграмме (см. рис. 15). Максимум интенсивности приходился на угол 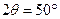 . Причём, для каждого кристалла угол, на который приходился максимум интенсивности, был своим. Во втором опыте при фиксированном угле падения электронного пучка на кристалл измерялась интенсивность отражённого пучка электронов в зависимости от энергии (т. е. От изменяющейся разности потенциалов). Интенсивность пучка отражённых электронов измерялась по силе тока между источником и детектором (см. рис. 15). Здесь стрелками показаны расчётные значения. Полученные зависимости соответствовали зависимостям, которые можно было бы получить, если бы исследовалась дифракция электромагнитной волны. Но, так как в эксперименте вместо волны использовались электроны, это дало возможность предположить, что дифракцию испытывают как раз они. Чуть позже были поставлены опыты Тартаковским и Томпсоном по исследованию дифракции электронов. Тартаковский использовал медленные электроны с энергией порядка 1,7 кэВ, а Томпсон – быстрые с энергиями 17,5 – 56,6 кэВ. Для наблюдения дифракции использовался метод Дебая – Шерера. В качестве кристалла они использовали металлическую поликристаллическую пластину. Рассеянные на ней электроны должны были дать интерференционную картину, то есть систему интерференционных колец, что было блестяще подтверждено в результате опыта. Существовало всё же некоторое опасение, что интерференционная картина вызвана вторичным рентгеновским излучением, которое получается при торможении электрона. Однако, если поместить мишень в магнитное поле, интерференционная картина, полученная с помощью рентгеновского излучения, не изменится, по сравнению со случаем отсутствия магнитного поля. В случае с электронами, картина должна получиться смазанной, что и имело место быть.
. Причём, для каждого кристалла угол, на который приходился максимум интенсивности, был своим. Во втором опыте при фиксированном угле падения электронного пучка на кристалл измерялась интенсивность отражённого пучка электронов в зависимости от энергии (т. е. От изменяющейся разности потенциалов). Интенсивность пучка отражённых электронов измерялась по силе тока между источником и детектором (см. рис. 15). Здесь стрелками показаны расчётные значения. Полученные зависимости соответствовали зависимостям, которые можно было бы получить, если бы исследовалась дифракция электромагнитной волны. Но, так как в эксперименте вместо волны использовались электроны, это дало возможность предположить, что дифракцию испытывают как раз они. Чуть позже были поставлены опыты Тартаковским и Томпсоном по исследованию дифракции электронов. Тартаковский использовал медленные электроны с энергией порядка 1,7 кэВ, а Томпсон – быстрые с энергиями 17,5 – 56,6 кэВ. Для наблюдения дифракции использовался метод Дебая – Шерера. В качестве кристалла они использовали металлическую поликристаллическую пластину. Рассеянные на ней электроны должны были дать интерференционную картину, то есть систему интерференционных колец, что было блестяще подтверждено в результате опыта. Существовало всё же некоторое опасение, что интерференционная картина вызвана вторичным рентгеновским излучением, которое получается при торможении электрона. Однако, если поместить мишень в магнитное поле, интерференционная картина, полученная с помощью рентгеновского излучения, не изменится, по сравнению со случаем отсутствия магнитного поля. В случае с электронами, картина должна получиться смазанной, что и имело место быть.
Дата добавления: 2016-01-30; просмотров: 981;
