Спектры непрерывных сигналов.
Вначале рассмотрим спектры непрерывного периодического сигнала с периодом Т. Для нахождения коэффициентов Фурье 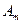 и
и 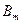 для такого сигнала следует задать предельные соотношения
для такого сигнала следует задать предельные соотношения 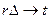 , т.е.
, т.е. 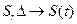 ;
; 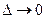 ;
; 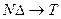 .
.
При этом выражения (5.3) принимают вид:
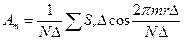 ;
; 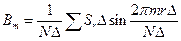 ,
,
или
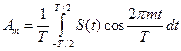 ;
; 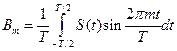 (5.10)
(5.10)
Формулы для амплитудного (5.4) и фазового (5.5) спектров непрерывного периодического сигнала остаются прежними, их характер также линейчатый, однако ввиду того, что 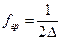 стремится к бесконечности, то число гармоник бесконечно. Комплексный спектр:
стремится к бесконечности, то число гармоник бесконечно. Комплексный спектр:
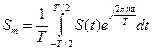 (5.11).
(5.11).
Соответственно, обратное преобразование Фурье: 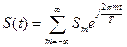 .
.
Средняя мощность сигнала, или его дисперсия, будет
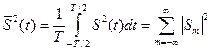 .
.
В качестве примера рассмотрим расчет спектра непрерывного сигнала прямоугольной формы с единичной амплитудой длительностью 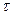 и с периодом
и с периодом 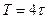 . Этот сигнал соответствует операции осреднения поля в окне размером
. Этот сигнал соответствует операции осреднения поля в окне размером 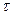 .
.
Коэффициенты Фурье такого сигнала равны
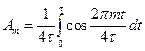 =
= 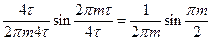 ;
;
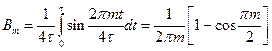 .
.
Соответственно, амплитудный спектр будет
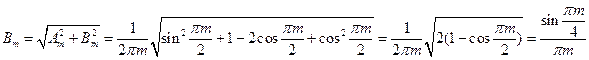
Фазовый спектр
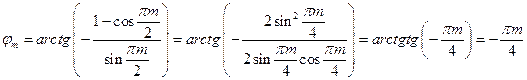 .
.
Перейдем к рассмотрению спектров непрерывного апериодического сигнала, т.е. когда 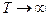 .
.
При этом коэффициенты Фурье (5.10) с учетом того, что 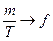 ;
; 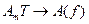 ,
, 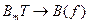 принимают вид:
принимают вид:
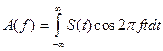 ;
; 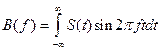 (5.12)
(5.12)
Комплексный спектр
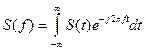 (5.13)
(5.13)
Обратное преобразование Фурье:
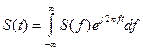 (5.14)
(5.14)
Если ввести круговую частоту 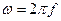 и выражение (5.14) умножить и разделить на
и выражение (5.14) умножить и разделить на 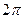 , то получим из (5.13) и (5.14) пару преобразований Фурье:
, то получим из (5.13) и (5.14) пару преобразований Фурье:
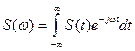
(5.15)
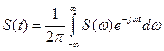
Дата добавления: 2016-01-16; просмотров: 1422;
