ГЛАВА VIII. ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ В ЗАДАЧАХ ОБНАРУЖЕНИЯ СЛАБЫХ СИГНАЛОВ.

Развитие теории статистических решений для обработки данных обусловлено следующими причинами. Критерии оптимальной фильтрации и соответствующие им алгоритмы обработки исходных данных обеспечивают выделение сигналов на фоне помех, однако принятие решения о наличии или отсутствии полезного сигнала после фильтрации осуществляется интерпретатором визуально. Это обстоятельство делает последний этап обработки весьма субъективным, особенно для случая обнаружения слабых сигналов. Под слабым сигналом понимается сигнал, соизмеримый по интенсивности с уровнем помех и ниже этого уровня. Визуальное обнаружение таких сигналов практически исключено. В то же время проблема обнаружения слабых сигналов в разведочной геофизике приобретает все большее значение в связи с поисками объектов, залегающих на больших глубинах, слабоконтрастных по физическим свойствам объектов, малоразмерных залежей углеводородов, а также объектов, аномальные эффекты от которых осложнены интенсивными помехами самой разной природы.

Получив в результате, например, согласованной фильтрации несколько положительных экстремумов, решение о наличии сигнала принимается лишь по максимальному из них. Относительно более слабых экстремумов решение о наличии сигнала принять трудно, поскольку в оптимальных фильтрах отсутствуют пороги принятия решения о наличии сигнала.

Вторая причина, по которой теория статистических решений получила развитие, связана с отсутствием общей теоремы, утверждающей, что максимальное отношение сигнал/помеха на выходе фильтра приводит к максимальному извлечению полезной информации. Под максимальным извлечением полезной информации в настоящее время принято понимать получение апостериорных вероятностей, в частности, для задачи обнаружения сигнала - апостериорных вероятностей наличия или отсутствия сигнала.

В теории статистических решений для решения задачи обнаружения используются те или иные критерии принятия статистических гипотез о наличии (отсутствии) сигнала, которые позволяют установить порог принятия решения о наличии сигнала, а также рассчитать апостериорные вероятности наличия сигнала. Оптимальная согласованная фильтрация при этом входит в качестве составной части алгоритмов теории статистических решений в задачах обнаружения слабых сигналов.

Основные понятия теории статистических решений.

Статистическое решение связано с понятием статистической гипотезы. При решении задачи обнаружения сигнала имеют место две статистические гипотезы:

- гипотеза о наличии сигнала, для которой наблюденные данные представляют сумму сигнала и помех 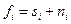. Эту гипотезу называют ненулевой и обозначают как Н₁, т.е. ;

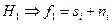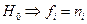- гипотеза об отсутствии сигнала, для которой наблюденные данные представлены только помехой, т.е. . Это - нулевая гипотеза Для каждой гипотезы по значениям 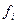можно построить статистический аналог плотности распределения - гистограмму. Такие плотности распределений значений 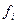называются функциями правдоподобия и обозначаются как 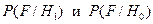, где 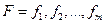. Функции правдоподобия для задачи обнаружения сигнала приведены на рис.8.1.

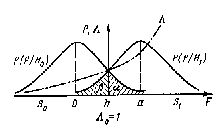Рис.8.1. Графики функций правдоподобия для гипотез Н0 и Н1.

При этом функция 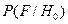соответствует оценке плотности распределения помех и в качестве гистограммы может быть построена на участках, на которых заведомо отсутствуют сигналы. Функция 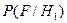будет смещена относительно 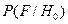на величину а, как это показано на рис.8.1. Всю область наблюденных значений 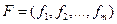можно разделить на две област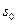и и 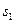величиной h. Область 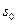соответствует множеству значений 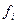для гипотезы 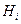. Величина h на оси 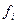, разделяющая эти области, называется порогом принятия решения о наличии той или иной гипотезы.

Принятие статистического решения о наличии сигнала не может быть безошибочным из-за осложнения сигнала помехами. При этом возникают ошибки двоякого рода.

Ошибка первого рода заключается в том, что принимается решение о наличии сигнала, т.е. о гипотезе Н₁, когда на самом деле сигнал отсутствует, т.е. выполняется гипотеза Н₀. Эта ошибка называется ошибкой обнаружения ложного сигнала. Она появляется тогда, когда наложение помех создает ситуацию, похожую на полезный сигнал.

Ошибка второго рода заключается в том, что принимается решение об отсутствии сигнала, т.е. о гипотезе Н₀, когда на самом деле сигнал имеется, т.е. выполняется гипотеза Н₁. Эта ошибка называется ошибкой пропуска сигнала. Она появляется тогда, когда помехи настолько искажают сигнал, что создается ситуация, отвечающая только помехе.

С ошибками первого и второго рода связаны соответствующие им вероятности.

Вероятность ошибки I рода или вероятность ошибки обнаружения ложного сигнала равна

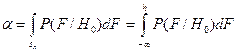(8.1)

Вероятность ошибки II рода или вероятность пропуска сигнала равна

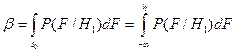(8.2)

Вероятност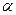и и 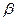соответствуют площадям, заштрихованным на рис. 8.1.

Если для гипотез Н₀ и Н₁ ввести их априорные вероятности р₀ и р₁, то общая безусловная вероятность ошибки, связанная как с обнаружением ложного сигнала, так и с пропуском сигнала, будет равна

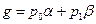(8.3)

Величина 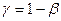называется вероятностью правильного обнаружения сигнала при его наличии или надежного обнаружения сигнала. Соответственно вероятность правильного необнаружения сигнала при его отсутствии равна .

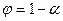При выборе порога h потери, обусловленные ошибками I и II рода, могут быть разными с точки зрения экономики. Если мы обнаруживаем ложный сигнал, то должны провести затраты на его проверку. В случае пропуска сигнала можно пропустить тот или иной важный объект поисков. Поэтому вводят цены для ошибок I и II рода - 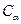и .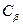

Произведение 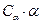называют риском(или потерей), соответствующим гипотезе Н₁. Средний риск или функция потерь при принятии решения определяется выражением:

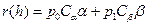(8.4),

в котором величина среднего риска зависит от значения порога h.