Критерии принятия статистических решений.
Естественный критерий принятия статистических решений связан с минимизацией среднего риска (8.4). Согласно критерию минимального риска, (он же называется критерием Байеса) выбирается такое значение порога h1, которое обеспечивает минимум выражения (8.4).
Для нахождения пороговой величины h выражение (8.4) перепишем с учетом (8.1) и (8.2) и к нему добавим и вычтем одну и ту же величину, равную 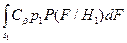 , т.е.
, т.е.
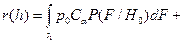
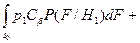
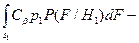
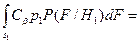
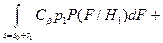
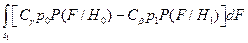 .
.
Поскольку в последнем выражении первый член равен  , то для минимизации r(h) нужно выбрать область s1 таким образом, чтобы под интегральная функция второго члена была бы отрицательной. Это приводит к тому, что
, то для минимизации r(h) нужно выбрать область s1 таким образом, чтобы под интегральная функция второго члена была бы отрицательной. Это приводит к тому, что 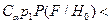
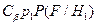 , или
, или
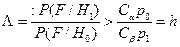 (8.5)
(8.5)
Отношение функций правдоподобия называют коэффициентом правдоподобия и обозначают его через 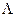 , для критерия минимального риска коэффициент правдоподобия в случае выполнения гипотезы Н1, т.е. гипотезы о наличии сигнала, должен превосходить величину порога h, равную
, для критерия минимального риска коэффициент правдоподобия в случае выполнения гипотезы Н1, т.е. гипотезы о наличии сигнала, должен превосходить величину порога h, равную 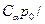
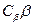 . Таким образом, применение критерия минимального риска возможно лишь при заданных ценах
. Таким образом, применение критерия минимального риска возможно лишь при заданных ценах 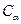 и
и 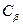 и априорных вероятностях гипотез р0 и р1. Поскольку достоверная оценка
и априорных вероятностях гипотез р0 и р1. Поскольку достоверная оценка 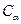 и
и 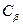 требует тщательного анализа большого статистического материала, который может быть получен лишь в районах с хорошей геолого-геофизической изученностью и экономических затрат на проверку ложных аномалий, то приходится считать, что
требует тщательного анализа большого статистического материала, который может быть получен лишь в районах с хорошей геолого-геофизической изученностью и экономических затрат на проверку ложных аномалий, то приходится считать, что 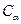 =
= 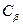 . При этом минимизируется общая безусловная вероятность ошибки (8.3), что приводит к критерию Котельникова (или критерию идеального наблюдателя), определяющего порог принятия решения в виде:
. При этом минимизируется общая безусловная вероятность ошибки (8.3), что приводит к критерию Котельникова (или критерию идеального наблюдателя), определяющего порог принятия решения в виде:
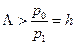 (8.6).
(8.6).
Если также принять априорные вероятности наличия и отсутствия сигнала равными (р0=р1), что отвечает максимальной неопределенности гипотез Н0 и Н1, то порог принятия решения будет равен единице, т.е.
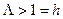 (8.7)
(8.7)
Что соответствует критерию максимального правдоподобия. Действительно, если найдены значения вероятностей 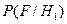 и
и 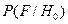 , то решение о наличии сигнала следует принять при
, то решение о наличии сигнала следует принять при 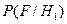 >
> 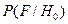 , что и приводит к выражению (8.7).
, что и приводит к выражению (8.7).
Критерий Котельникова, при заданных р0 и р1, позволяет на основе формулы Байеса оценить апостериорную вероятность наличия сигнала:
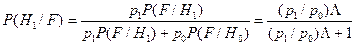
Решение о наличии сигнала принимается при максимальной величине 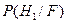 . Такой критерий называется критерием максимума апостериорной вероятности. Очевидно, что при р0=р1, критерий максимума апостериорной вероятности приводит к пороговой величине
. Такой критерий называется критерием максимума апостериорной вероятности. Очевидно, что при р0=р1, критерий максимума апостериорной вероятности приводит к пороговой величине 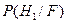 , равной 0,5, т.е. при р0=р1,
, равной 0,5, т.е. при р0=р1, 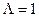 и
и 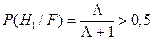 для гипотезы Н1.
для гипотезы Н1.
Правило принятия решения при отсутствии сведений об априорных вероятностях приводит к критерию Неймана-Пирсона. Согласно этому критерию минимизируется величина 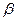 при условии задания вероятности обнаружения ложного сигнала
при условии задания вероятности обнаружения ложного сигнала 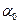 , т.е. при
, т.е. при 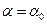 , min
, min 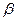 .
.
Очевидно, что при заданной вероятности ошибки I рода и найденной функции правдоподобия 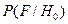 нетрудно найти порог принятия решения h из выражения
нетрудно найти порог принятия решения h из выражения 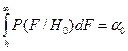 .
.
При обработке геофизических данных с целью обнаружения слабых сигналов наибольшее применение нашли три критерия: критерий максимального правдоподобия, критерий максимума апостериорной вероятности и критерий Неймана-Пирсона.
Кроме перечисленных критериев известны также критерий минимакса, при котором порог h находится при минимизации максимально возможного риска, критерий Вальда (или критерий последовательного анализа), при котором задаются вероятности 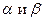 , что приводит к двум пороговым величинам
, что приводит к двум пороговым величинам 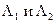 и решение о наличии сигнала принимается при
и решение о наличии сигнала принимается при 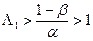 .
.
Критерий минимакса является достаточно грубым в том смысле, что принятие решения о наличии сигнала можно принимать просто визуально, а критерий Вальда требует непрерывного расчета пороговых величин 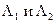 при каждом новом измеренном значении поля.
при каждом новом измеренном значении поля.
8.3.Коэффициент правдоподобия и вероятности
ошибок I и II рода.
Коэффициент правдоподобия определяется через функции правдоподобия. Посредством коэффициента правдоподобия вычисляются вероятности ошибок обнаружения ложного сигнала и пропуска сигнала, а также важная характеристика надежности обнаружения сигнала. Кроме того, коэффициент правдоподобия лежит в основе одного из способов обнаружения слабых сигналов – способа обратных вероятностей.
Нахождение коэффициента правдоподобия обычно проводится для нормально распределенной помехи. Согласно центральной предельной теоремы сумма произвольно распределенных случайных величин, при их числе более девяти, распределена нормально, т.е. свертка, представляющая сумму произведения исходных данных, как случайных величин, на весовые коэффициенты, имеет также нормальное распределение. Это обстоятельство при расчете коэффициента правдоподобия имеет принципиальное значение.
Найдем выражение для коэффициента правдоподобия, полагая распределение некоррелированной помехи нормальным с нулевым средним и дисперсией 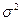 , а сигнал заданным по форме. При этом получим следующие выражения для функций правдоподобия:
, а сигнал заданным по форме. При этом получим следующие выражения для функций правдоподобия: 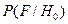 и
и 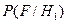 , учитывая, что гипотеза Н0 состоит в том, что
, учитывая, что гипотеза Н0 состоит в том, что 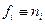 , а гипотеза
, а гипотеза 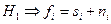 (
( 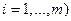 .
.
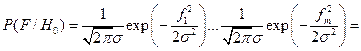
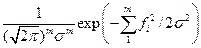 .
.
Поскольку 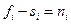 , то
, то
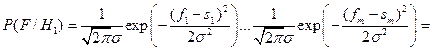
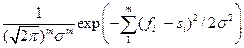 .
.
Соответственно, коэффициент правдоподобия будет равен
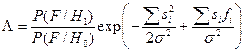 (8.7),
(8.7),
где первый член под экспонентой 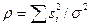 определяет энергетическое отношение сигнал/помеха для некоррелированной помехи, а второй член
определяет энергетическое отношение сигнал/помеха для некоррелированной помехи, а второй член 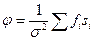 - есть корреляционная сумма сигнала с исходными значениями поля.
- есть корреляционная сумма сигнала с исходными значениями поля.
Согласно приведенным выше критериям решение о наличии сигнала принимается при 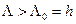 . Тогда, прологарифмировав выражение (8.7), получаем
. Тогда, прологарифмировав выражение (8.7), получаем
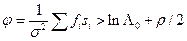 .
.
Вероятность ошибки обнаружения ложного сигнала  - это вероятность того, что при отсутствии сигнала величина
- это вероятность того, что при отсутствии сигнала величина 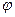 окажется больше порога
окажется больше порога 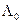 и будет принято неправильное решение о наличии сигнала, т.е. при
и будет принято неправильное решение о наличии сигнала, т.е. при 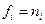 ,
, 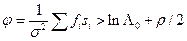 .
.
Иначе для вычисления вероятности  надо определить вероятность последнего неравенства. Поскольку помеха ni – некоррелирована и имеет нормальное распределение с нулевым средним и дисперсией
надо определить вероятность последнего неравенства. Поскольку помеха ni – некоррелирована и имеет нормальное распределение с нулевым средним и дисперсией 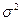 , величина
, величина 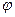 будет нормально распределена со средним
будет нормально распределена со средним 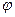 =0 и дисперсией
=0 и дисперсией 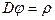 .
.
Следовательно, вероятность ошибки I рода с
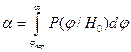
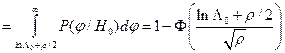 (8.8) ,
(8.8) ,
где 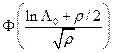 - интеграл вероятности:
- интеграл вероятности: 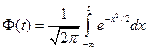 , нормировка в (8.8) на величину
, нормировка в (8.8) на величину 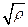 необходима для приведения
необходима для приведения 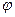 к единичной дисперсии.
к единичной дисперсии.
Аналогично находим вероятность ошибки пропуска сигнала 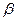 . При этом величина
. При этом величина 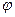 будет меньше порога
будет меньше порога 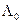 , несмотря на наличие сигнала, т.е. при
, несмотря на наличие сигнала, т.е. при 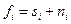
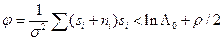 , причем среднее значение
, причем среднее значение 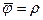 и
и 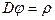 .
.
Вероятность ошибки II рода
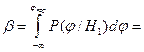
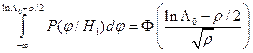 (8.9)
(8.9)
В выражении (8.9) учтено приведение распределения 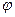 в интеграле вероятности к нулевому среднему и единичной дисперсии, т.е. следует из
в интеграле вероятности к нулевому среднему и единичной дисперсии, т.е. следует из 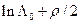 вычесть среднее значение, равное
вычесть среднее значение, равное 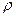 и произвести нормировку на
и произвести нормировку на 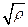 .
.
Для критерия максимального правдоподобия порог 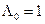 и из выражений (8.8) и (8.9) следует, что
и из выражений (8.8) и (8.9) следует, что 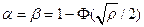 .
.
Для критерия Неймана-Пирсона порог принятия решения 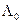 находится при заданных значениях
находится при заданных значениях 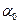 и
и 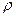 , а именно:
, а именно: 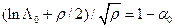 . Если
. Если 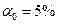 , то
, то 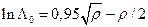 .
.
Дата добавления: 2016-01-16; просмотров: 1627;
