Способ обратных вероятностей.

Способ обратных вероятностей предназначен для обнаружения слабых сигналов известной формы. В отличие от согласованного фильтра, также реализующего обнаружение заданных по форме сигналов, он включает порог принятия решения о наличии сигнала и вычисление апостериорных (обратных) вероятностей наличия сигнала по формуле Байеса, известной как формула обратных вероятностей. Это и определило название способа, впервые для решения задач разведочной геофизики, предложенного А.Г.Тарховым в 1959 г.

В связи с развитием вейвлет-анализа применение способа обратных вероятностей приобретает особое значение.

Рассмотрим обнаружение заданного по форме сигнала на фоне некоррелированной помехи с позиции теории статистических решений.

1. Постановка задачи и модель поля.

Задача обработки состоит в обнаружении сигнала, соизмеримого с уровнем помех или ниже этого уровня. Модель поля 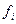представляет сумму сигнала 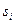и помехи 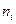. Форма сигнала считается заданной, помеха предполагается в виде стационарного случайного процесса, некоррелированной и нормально распределенной с нулевым средним и дисперсией 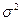. Требуется по последовательности измеренных значений поля 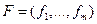с определенной вероятностью установить, является ли та последовательность суммой сигнала и помехи, или она представлена лишь одной помехой, что приводит к сравнению двух гипотез 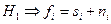и .

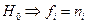2. Оценка формы сигнала и свойств помехи.

Форма сигнала может быть получена либо путем решения прямой задачи для выбранной физико-геологической модели искомого объекта и вмещающей среды, либо просто по наблюдаемым визуально сигналам на соседних или сходных по геологическому строению объектах. Оценка корреляционных свойств помехи осуществляется на заведомо безаномальных участках съемки путем расчета АКФ, на основе которой делается вывод о некоррелируемом или коррелируемом характере помехи с определением ее дисперсии .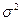

3. Выбор критерия принятия решения о наличии сигнала.

Для обнаружения заданного по форме сигнала наиболее предпочтителен критерий максимального правдоподобия, при котором априорные вероятности наличия и отсутствия сигнала равны по 0,5. Согласно этому критерию задача обнаружения сигнала будет сведена к расчету коэффициента правдоподобия 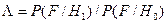и его сравнению с порогом 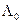, равным единице. При 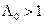принимается решение о наличии сигнала. От коэффициента правдоподобия с использованием формулы Байеса легко перейти к вычислению апостериорной вероятности гипотезы о наличии сигнала, т.е. от условной вероятности 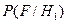к условной (апостериорной) вероятности 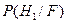, т.е. к обратной вероятности, а именно:

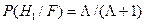(8.13)

С учетом критерия максимального правдоподобия при пороге принятия решения 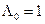, получаем правило (критерий) принятия решения о наличии сигнала по величине апостериорной вероятности (критерий максимума апостериорной вероятности) 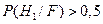- есть сигнал. При принимается решение об отсутствии сигнала.

4. Алгоритм обнаружения сигнала.

Для случая некоррелированной помехи, нормально распределенной с нулевым средним и дисперсией 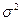, в разделе 8.2 было получено выражение для коэффициента правдоподобия в виде

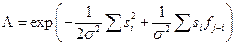(8.14),

где индекс j характеризует смещение сигнала вдоль профиля от точки к точке.

Решение о наличии сигнала при этом принимается по величине апостериорной вероятности

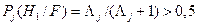(8.15).

Выражение (8.14) и (8.15) и представляют алгоритм способа обратных вероятностей.

В (8.14) первый член под знаком экспоненты определяет энергетическое отношение сигнал/помеха 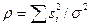, и при вычислениях он остается неизменным, а второй член является сверткой, обеспечивающей реализацию согласованного фильтра, т.е. процесс обнаружения по критерию максимума пикового отношения сигнал/помеха. Весовой функцией при обнаружении служат ординаты сигнала, нормированные на дисперсию помехи 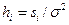. В качестве примера реализации вычислений по формулам (8.14) и (8.15) рассмотрим обнаружение сигнала, заданного ординатами 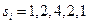в числовом поле из двенадцати значений 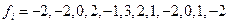. Среднее значение 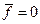, дисперсия 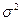=3. Ни одно из приведенных значений сигнала не превосходит тройную погрешность наблюдений 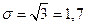, а дисперсия сигнала 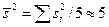не превосходит даже двойную величину .

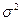Энергетическое отношение сигнал/помеха равно 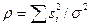=26/3=8,67, что соответствует достаточно высокой надежности обнаружения такого сигнала по критерию максимального правдоподобия, равной 93%.

Нахождение результатов свертки в (8.14) осуществляется как 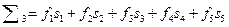; 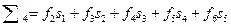и т.д., где получаемые суммы относятся к центральной точке перемещаемого сигнала.

Расчеты по формулам (8.14) и (8.15) можно свести к таблице 1, в которой последний столбец оценивает апостериорные вероятности наличия сигнала. Решение о наличии сигнала принимается лишь для точки с номером 6, в которой величина апостериорной вероятности 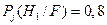, т.е. она больше порогового значения, равного 0,5.

Таблица 1.

№ точки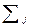
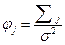
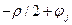
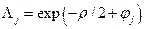
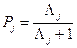
	-3 -3 -3	-1.00 2.33 2.33 5.67 4.33 2.33 -1.00 -1.00	-5.34 -2.01 -2.01 1.33 -0.01 -2.01 -5.34 -5.34	0.13 0.13 3.78 0.99 0.13	0.12 0.12 0.80 0.50 0.12

Обнаружение сигнала на фоне коррелированных помех включает те же самые процедуры вычислений. Отличие состоит в том. что вместо величины 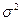для помехи следует рассчитать корреляционную матрицу помехи 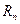по ее АКФ. Алгоритм обнаружения при этом сводится к вычислению коэффициента правдоподобия

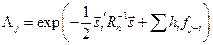(8.16).

где весовые коэффициенты 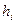являются решением системы линейных уравнений 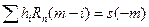. т.е. определяются аналогично согласованному фильтру.

Способ обратных вероятностей эффективен при обнаружении сигналов. соизмеримых с уровнем помех. при достаточной их протяженности по профилю 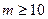и лишь для случая некоррелированной помехи. Для более слабых сигналов следует привлекать способы межпрофильной и самонастраивающейся фильтрации.