Надежность обнаружения сигнала и ее применение.

Надежность обнаружения сигнала 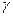определяется как вероятность правильного обнаружения сигнала при его наличии и равна .

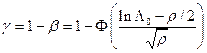Для критерия максимального правдоподобия, т.е. когда порог 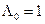, надежность обнаружения будет

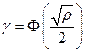(8.10) ,

где 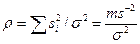- энергетическое отношение сигнал/помеха, а 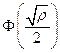- интеграл вероятности.

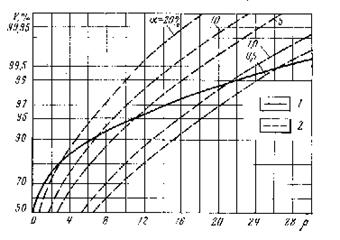Рис.8.2. Характеристики обнаружения сигнала -по критерию максимального правдоподобия (1); -по критерию Неймана-Пирсона (2);

Характеристики обнаружения сигнала, представляющие зависимости между надежностью обнаружения 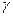и энергетическим отношением для критерия максимального правдоподобия (8.10) и для критерия Неймана-Пирсона при заданных величинах 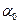и 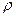приведены на рис.8.2. Характеристики обнаружения сигнала иллюстрируют тот факт, что для достижения большей надежности требуется и большее отношение сигнал/помеха. Это достаточно известный факт здесь описывается количественной зависимостью величины 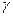от .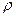

Характеристики обнаружения позволяют еще до начала обработки оценить возможность выявления тех или иных сигналов (аномалий). Например, надежность обнаружения сигнала, соизмеримого с уровнем помех, т.е. 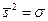при 10 аномальных значениях по критерию максимального правдоподобия равна 95%, т.к. 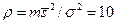. Для критерия Неймана-Пирсона при одном и том же отношении 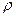обнаружение характеризуется разной надежностью в зависимости от заданной величины 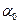, как это показано на рис.8.2.

Выражения (8.8), (8.9) и (8.10) справедливы для случая обнаружения сигнала на фоне некоррелированной помехи. При коррелированной помехе энергетическое отношение сигнал/помеха определяется соотношением:

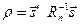(8.11)

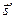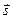, где и - вектор-строка и вектор-столбец значений сигнала, 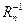- обратная корреляционная матрица помехи. Корреляционная матрица помехи 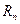строится по АКФ помехи. Таким образом, одно из применений надежности обнаружения сигнала состоит в оценке качества выявляемых аномальных эффектов.

Заметим, что если форма сигнала неизвестна, то оценка энергетического отношения сигнал/помеха, а, следовательно, и надежность обнаружения сигнала, может быть проведена непосредственно по исходным значениям поля с использованием ВКФ и интервала корреляции, рассчитанного по АКФ. По функциям взаимной корреляции в предположении коррелированности сигнала от профиля к профилю (от трассы к трассе) рассчитывается величина 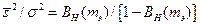, где 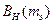- значение положительного экстремума ВКФ. Протяженность сигнала m оценивается по величине интервала корреляции, определяемого по АКФ. Следовательно, энергетическое отношение сигнал/помеха 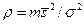. Эта оценка 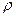является усредненной для некоторого среднестатистического сигнала, тем не менее, она позволяет до начала обработки или после обработки определить надежность обнаружения сигнала.

Другим практическим приложением надежности обнаружения является четкое определение понятия достоверная геофизическая аномалия или достоверный сигнал. Так, согласно действующим инструкциям по магнито-, электро- и гравиразведке, под аномалией (достоверной) понимается совокупность не менее трех точек со значениями поля, превышающими тройную среднеквадратическую погрешность наблюдений 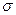, т.е. когда m=3; 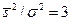. При этом определении величина энергетического отношения сигнал/помеха будет равна 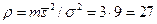. По критерию максимального правдоподобия надежность обнаружения сигнала при 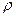=27 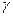>99,5%. Из тех же соображений аномалия с отношением 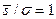будет достоверной при 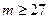. Интуитивно предполагая наличие связи с надежностью обнаружения сигнала и числом его аномальных значений на практике сгущают сеть наблюдений с целью увеличения достоверности обнаружения сигнала. При этом интерпретаторы пренебрегают условием о наличии трех точек со значениями поля, большими 3 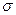, когда речь идет о выделении протяженных слабопроявленных аномалий и, как следует, из приведенных выше расчетов надежности обнаружения такой подход является вполне оправданным.

При проведении радиометрической съемки за аномалию, согласно инструкции по пешеходной гамма-съемке, принимается лишь одна точка (m=1) со значениями естественной радиоактивности 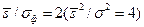, где 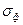- среднеквадратический уровень фона пород. При этом надежность ее обнаружения по формуле (8.10) равна 84%. Следовательно, в определении понятия достоверная аномалия необходимо объединить разные подходы, что можно осуществить на базе надежности обнаружения сигнала (8.10), а именно: «под достоверной аномалией следует понимать такую составляющую поля, отношение энергии которой к мощности помех (в частности, к дисперсии помех) 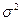превосходит порог, соответствующий заданной вероятности, т.е. надежности обнаружения ».

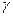Следующим практическим приложением надежности обнаружения сигнала является возможность получения объективного критерия для выбора параметров геофизической съемки (шага съемки).

Из выражения (8.10) следует, что

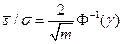(8.12)

где 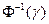- аргумент интеграла вероятности. Тогда, задавая величину надежности обнаружения сигнала 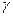от интересующего нас объекта из выражения (8.12) можно найти число характеризующих наблюдений для сигнала m, что приводит к необходимому значению шага съемки. При этом величина 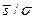оценивается предварительно путем решения прямой задачи, либо по функциям взаимной корреляции данных, полученных при опытно-методических работах. Отметим, что при одном и том же отношении 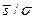для увеличения надежности обнаружения сигнала 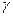требуется большее число наблюденных его значений, и такая зависимость выражена количественно.

При всех выводах, которые следовали из анализа надежности обнаружения сигнала, мы исходили из предположения отсутствия корреляции помехи. Только при этом надежность обнаружения растет пропорционально увеличению числа аномальных значений поля, поскольку 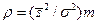, т.е. на определенной стадии детализации аномалии, увеличение числа m не будет приводить к увеличению 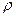, поскольку уменьшение шага съемки (увеличение числа m на одном и том же интервале) приведет в конечном итоге к коррелированности помех, обусловленной в частности, эффектами от поверхностных неоднородностей.

Влияние коррелированности помех проиллюстрируем на примере АКФ помехи треугольного типа, для которой дисперсия коррелированной помехи определяется соотношением 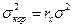, где 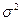- дисперсия некоррелированной помехи, а r – интервал корреляции помехи по профилю. Следовательно, энергетическое отношение сигнал/помехи 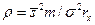. При этом сгущение сети путем увеличения m будет скомпенсировано возрастанием величины интеграла корреляции помехи 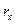, и выигрыша в увеличении энергетического отношения не будет.

Однако, остается еще путь повышения надежности обнаружения сигнала за счет увеличения числа независимых его наблюдений по нескольким профилям. Тогда энергетическое отношение 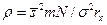, где число N – число профилей, по которым прослеживается сигнал.

В то же время вновь на определенном этапе сгущения сети профилей возникнет корреляция помехи уже между профилями, т.е. увеличение числа независимых наблюдений сигнала за счет увеличения числа профилей N будет скомпенсировано ростом интервала корреляции помехи между профилями .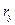

Наконец, увеличение надежности обнаружения сигнала может быть достигнуто путем использования данных комплекса геофизических методов. Если для каждого независимого физического поля сигнал обусловлен одним и тем же геологическим объектом, надежность обнаружения определяется выражением 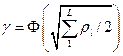, где 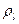- отношение сигнал/помеха для l-го поля, l=1,…,L – число полей или число независимых между собой атрибутов одного и того же поля.