Байесовский критерий обнаружения сигнала

Классическая теория обнаружения сигналов в качестве критерия оптимальности использует старинное изобретение английского священника и математика Томаса Байеса – критерий минимума среднего риска, изложенный им в "Эссе о решении проблем в теории случайных событий".

Будем считать, что a priori известны:

1. условные совместные плотности распределения шума 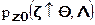и аддитивной смеси сигнала и шума ,

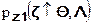2. вероятности 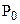отсутствия сигнала в наблюдаемой реализации сигнала 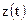и наличия в ней сигнала ,

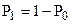3. платежная матрица 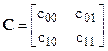с элементами 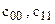- расходы на принятие правильного решения и 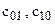- плата за ошибки первого и второго рода.

С учетом выражений для вероятностей принятия верных решений и вероятностей ошибок среднее значение потерь, то есть средний риск, связанный с принятием решения, составляет:

.

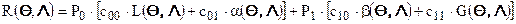Подставляя сюда выражения для вероятностей ошибок первого и второго рода, а также выражения для оперативной характеристики и функции мощности, после некоторых преобразований получаем следующую зависимость:

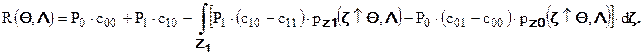Отсюда видно, что критическую область 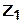нужно выбирать таким образом, чтобы подынтегральное выражение было хотя бы неотрицательным:

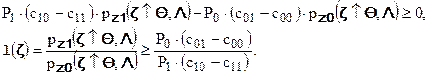
Функция 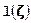после подстановки в неё вместо вектора 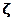наблюденных данных 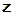называется отношением правдоподобия 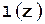. Отношение правдоподобия преобразует комплекс экспериментальных данных 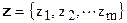в некоторое число, на основании которого и принимается решение по поводу обнаружения или отсутствия сигнала на фоне помех.

Оптимальная по критерию минимума среднего риска функция потерь имеет, поэтому, следующий вид:

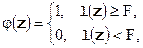где 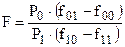пороговая константа.

Решение о присутствии сигнала в наблюдаемой выборке принимается, если отношение правдоподобия для этой выборки оказывается не меньшим, чем пороговая константа. Пороговая константа разбивает n-мерное пространство всех возможных выборок 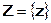на две непересекающихся област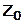и и 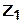, , 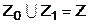такие, что в критической области 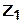выполняется условие 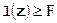, а в допустимой области 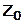имеет место .

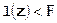В задаче обнаружения сигнала синусоидальной формы с вектором параметров сигнала 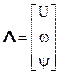на фоне независимой от сигнала нормально распределенной помехи типа белого шума с одноместным вектором параметров 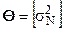при полученной путем дискретизации наблюдаемой реализации сигнала z(t) выборке 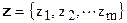отношение правдоподобия принимает следующий вид:

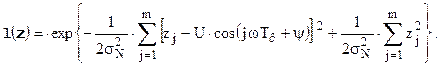
Часто, особенно при экспоненциальных функциях распределения, пользуются логарифмической функцией правдоподобия 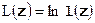, которая получается логарифмированием отношения правдоподобия. В рассматриваемом случае логарифмическая функция правдоподобия имеет вид, особенно удобный для практических расчетов:

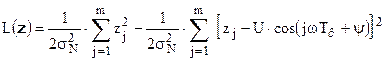
с пороговой константой, равной .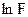

Недостаточность априорной информации в реальных ситуациях и возможность появления аномально больших искажений при наблюдении за сигналом требует построения более сложных алгоритмов обнаружения сигналов. Поиск таких алгоритмов и является задачей теории обнаружения и различения сигнала.