Временная фильтрация
Будем по-прежнему считать, что принимаемый сигнал – это радиоимпульс:
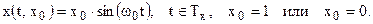
Принимаемый сигнал является аддитивной смесью сигнала и шума:
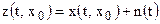 .
.
Определим автокорреляционную функцию этой смеси:
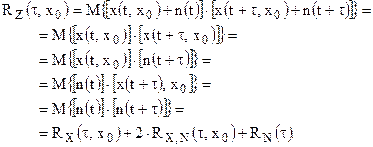
Если сигнал и шум не коррелированны, то их взаимнокорреляционная функция 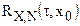 равна нулю, и поэтому автокорреляционная функция аддитивной смеси сигнала и шума равна сумме их автокорреляционных функций:
равна нулю, и поэтому автокорреляционная функция аддитивной смеси сигнала и шума равна сумме их автокорреляционных функций:
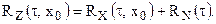
 |
Если x(t) – синусоидальный сигнал со случайной фазой, то его автокорреляционная функция является косинусоидой той же частоты:
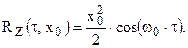
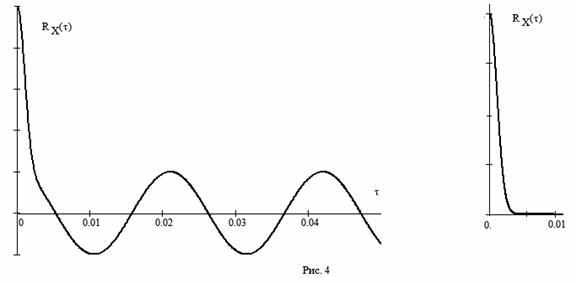
Автокорреляционная функция шума 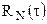 обычно быстро убывает с ростом τ, а для белого шума имеет форму δ – функции при τ=0. Поэтому автокорреляционная функция синусоидального сигнала на фоне почти белого шума будет всегда выглядеть так, как это показано на рис. 4 слева. При отсутствии сигнала (
обычно быстро убывает с ростом τ, а для белого шума имеет форму δ – функции при τ=0. Поэтому автокорреляционная функция синусоидального сигнала на фоне почти белого шума будет всегда выглядеть так, как это показано на рис. 4 слева. При отсутствии сигнала ( 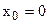 ) автокорреляционная функция будет просто быстро затухать, как на рис. 4 справа. Отсчет значения автокорреляционной функции по истечении времени
) автокорреляционная функция будет просто быстро затухать, как на рис. 4 справа. Отсчет значения автокорреляционной функции по истечении времени 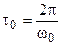 в первом случае даст значение
в первом случае даст значение 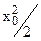 , а во втором случае – нуль.
, а во втором случае – нуль.
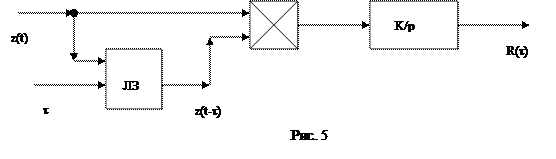 |
Это обстоятельство и положено в основу построения временных (корреляционных) фильтров. Схема построения фильтра представлена на рис. 5.
 Фильтр состоит из линии задержки на время
Фильтр состоит из линии задержки на время 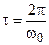 , схемы перемножения принимаемого сигнала и сигнала на выходе линии задержки и интегратора, обеспечивающего интегрирование результата перемножения по времени в пределах от 0 до
, схемы перемножения принимаемого сигнала и сигнала на выходе линии задержки и интегратора, обеспечивающего интегрирование результата перемножения по времени в пределах от 0 до 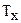 , после чего интегратор обнуляется и вновь включается в момент ожидаемого прихода нового радиоимпульса. Название этого устройства фильтром является в большой степени условным, поскольку он осуществляет не преобразование сигнала, а только вычисление фиксированных значений его автокорреляционной функции.
, после чего интегратор обнуляется и вновь включается в момент ожидаемого прихода нового радиоимпульса. Название этого устройства фильтром является в большой степени условным, поскольку он осуществляет не преобразование сигнала, а только вычисление фиксированных значений его автокорреляционной функции.
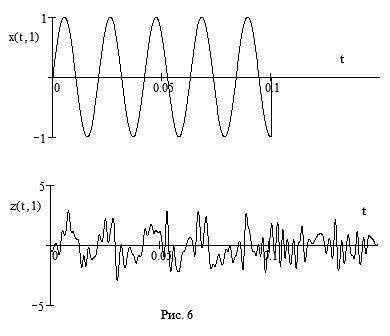
В качестве примера на рис. 6 представлены графики ожидаемого сигнала x(t, 1) и аддитивной смеси 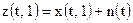 сигнала и шума n(t), единственно доступной для наблюдения. Нижний график на рис. 6 наглядно показывает, как сигнал почти полностью теряется на фоне шума.
сигнала и шума n(t), единственно доступной для наблюдения. Нижний график на рис. 6 наглядно показывает, как сигнал почти полностью теряется на фоне шума.
Расчеты, реализуемые фильтром, дают при этом следующие значения выходного сигнала соответственно при наличии и отсутствии сигнала, подлежащего обнаружению:

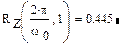
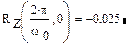
При наличии сигнала ( 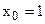 ) выходной сигнал корреляционного фильтра принимает значение 0,445, то есть примерно значение, равное половине квадрата амплитуды, а в условиях отсутствия сигнала (
) выходной сигнал корреляционного фильтра принимает значение 0,445, то есть примерно значение, равное половине квадрата амплитуды, а в условиях отсутствия сигнала ( 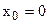 ) значение сигнала составляет всего-то -0,025.
) значение сигнала составляет всего-то -0,025.
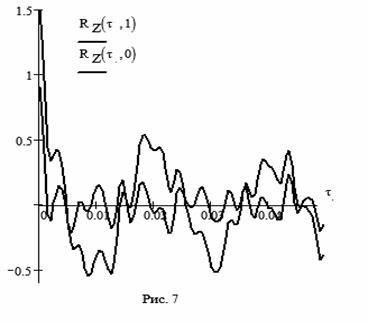 На рис. 8 представлены графики изменения корреляционных функций шума (синяя линия) и смеси сигнала и шума (красная линия), рассчитанные в соответствии с данными, изображенными на рис. 6. Представленные кривые повторяют то, что было представлено на рис. 4, но соответствуют не только теоретическим выводам, но и практическим результатам расчетов.
На рис. 8 представлены графики изменения корреляционных функций шума (синяя линия) и смеси сигнала и шума (красная линия), рассчитанные в соответствии с данными, изображенными на рис. 6. Представленные кривые повторяют то, что было представлено на рис. 4, но соответствуют не только теоретическим выводам, но и практическим результатам расчетов.
Дата добавления: 2015-11-28; просмотров: 2208;
