Временная сложность алгоритма. Классы P и NP.

При решении массовой задачи P требуется не просто найти алгоритм, решающий эту задачу, но построить наиболее эффективный алгоритм.

Под эффективностью алгоритма понимают все вычислительные ресурсы, необходимые для работы алгоритма. Так как ограничения по времени являются детерминирующими, то основное внимание сосредотачивается на этом ресурсе. Временная сложность алгоритма является одной из важнейших характеристик алгоритма, которая определяет затраты машинного времени на его реализацию. Кроме временной сложности алгоритма анализируется еще и сложность по памяти.

Временная сложность алгоритма отражает требующиеся для его работы затраты времени. Время работы алгоритма удобно выражать в виде функции от переменной, характеризующей размер индивидуальной задачи (размерности задачи) т.е. объём данных, требуемых для описания этой задачи. Например, для графа, задаваемого списками инцидентности, размерность задачи представляется как пара (n,m). Эта функция каждой входной длине n ставит в соответствие максимальное время, затрачиваемое алгоритмом на решение индивидуальной задачи этой длины. Значение времени зависит от схемы кодирования и вычислительного устройства, определяющего время работы. Нас же будет в дальнейшем интересовать не точная временная сложность алгоритма, а асимптотическая сложность, которая определяется скоростью роста числа шагов алгоритма при неограниченном увеличении размерности задачи.

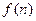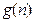Для сравнения скорости роста двух функций и будем использовать обозначения 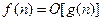или .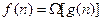

Будем говорить, что функция 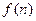имеет порядок роста не более, чем функция 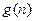, что обозначается 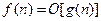, тогда и только тогда, когда существуют 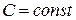и 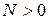, такие, что

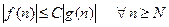
Будем говорить, что функция 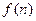имеет порядок роста не менее, чем функция 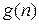, что обозначается 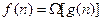, тогда и только тогда, когда существуют 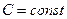и 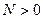, такие, что

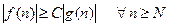
Например, для функции

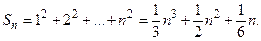
в силу принятых обозначений, можно записать, что 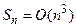или 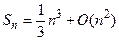. В общем случае, если 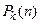- многочлен степени: 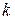, то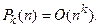

Непосредственно из определения вытекают следующие свойства:

;

;

.

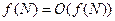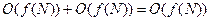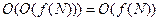Если рассматривается представление алгоритма, как ДМТ-программа M, то временная сложность алгоритма 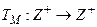определяется равенством .

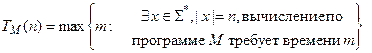ДМТ-программа M называется полиномиальной, если существует полином некоторой степени k, такой что 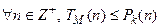, т.е. 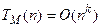. С помощью этого понятия введём класс языков P.

Класс языков P образуют языки, для которых существует полиномиальная ДМТ-программа распознавания, т.е.

.

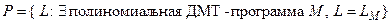Будем говорить, что задача распознавания P принадлежит классу задач P при схеме кодирования e, если язык 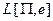принадлежит классу языков P.

Однако не для любой задачи полиномиальная программа существует. Рассмотрим, например, задачу коммивояжера. Как задача распознавания она формулируется следующим образом: дано множество городов, расстояния между ними и граница B, существует ли проходящий через все города маршрут длины, не превосходящей B. Полиномиальный алгоритм решения этой задачи неизвестен. Опишем вначале неформально класс задач, к которому она принадлежит, а потом формализуем это определение.

Неформально класс NP можно определить с помощью недетерминированного алгоритма. Он состоит из 2-х стадий: угадывания и проверки. По индивидуальной задаче I происходит угадывание структуры S, для задачи о коммивояжере такой структурой является вариант пути между вершинами графа. Затем I и S подаются на стадию проверки, которая выполняется детерминированным образом. В нашем примере проверяется, является ли предъявленный путь гамильтоновым циклом, вычисляется его длина и сравнивается с границей B.

Недетерминированный алгоритм решает задачу распознавания P, если 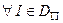выполняются свойства:

1) Если 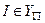, то $ структура S, угадывание которой приводит к положительному ответу;

2) Если 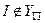, то такой структуры не существует.

Таким образом, класс задач NP – это класс всех задач распознавания, которые при разумном кодировании могут быть решены недетерминированным алгоритмом за полиномиальное время.

Формальным эквивалентом для недетерминированного алгоритма является программа для недетерминированной одноленточной машины Тьюринга (НДМТ). Структура НДМТ отличается от ДМТ наличием угадывающего модуля со своей читающе/пушущей головкой, связанного с управляющим устройством. Программа для НДМТ задаётся тем набором 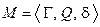, что и для ДМТ.

Порядок работы НДМТ под управлением программы .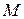

1. Входное слово 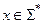записывается на ленте в ячейках с номерами 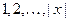( 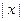– длина слова x), все другие ячейки содержат пустой символ. Читающая/пишущая головка управляющего устройства находится над ячейкой с номером 1, а угадывающего модуля – над ячейкой -1.

2. Управление передаётся угадывающему модулю, который записывает результат работы на левую полуленту и переходит в пассивное состояние.

3. Управляющее устройство начинает работу в состоянии .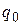

4. Если текущее состояние q не совпадает с одним из конечных состояний, то машина переходит в следующее состояние, определяемое согласно функции переходов. Пусть 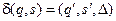, где s – считанный головкой символ из текущей ячейки. Тогда управляющее устройство переходит в состояние 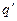, головка вместо символа s записывает символ 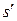и сдвигается на одну ячейку влево, если 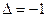, или вправо, если 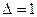. Затем, текущим становится состояние .

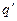5. Если 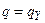, то вычисления заканчиваются с результатом “да”, если 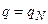, то – с результатом “нет”.

НДМТ-программа может иметь бесконечное число вычислений при заданном входе x, по одному для каждого слова-догадки из G^*. НДМТ-программа принимает x, если по крайней мере одно из вычислений на входе x является принимающим.

Временная сложность НДМТ-программы определяется равенством

.

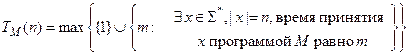НДМТ-программа называется НДМТ-программой с полиномиальным временем работы, если существует полином некоторой степени k, такой что .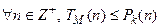

Класс языков NP формально определяется как

.

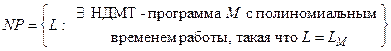Задача называется труднорешаемой, если для неё не существует полиномиального алгоритма. Все задачи, труднорешаемость которых доказана, являются либо алгоритмически неразрешимыми, либо труднорешаемыми недетерминированной машиной.

Не существует алгоритма, который по номеру x любого алгоритма и исходным данным y определяет, остановится ли данный алгоритм при этих данных.

Алгоритмически неразрешимой является 10-я проблема Гильберта: существует ли целочисленное решение произвольного заданного полиномиального уравнения.