Рекурсивные функции

Очевидно, что вычислимыми являются все натуральные константы. Как и в формальной арифметике натуральных чисел, определим их с помощью константы 0 и функции следования .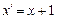

Также вычислимыми являются функции тождества. Через 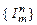обозначим множество функций, вычисляемых по правилу

.

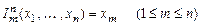Мощным средством построения новых функций является их суперпозиция.

Определение. Оператором суперпозиции 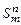называется подстановка в функцию от m переменных m функций от одних и тех же n переменных, т.е. 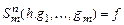, где и .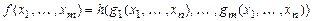

Функции тождества и оператор суперпозиции задают всевозможные операторы подстановки функции в функцию, а также переименования, перестановки и отождествления переменных.

Оператор примитивной рекурсии определяет n+1-местную функцию f через n-местную функцию g и n+2-местную функцию h.

Определение. Система равенств

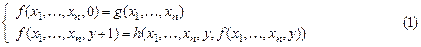
называется схемой примитивной рекурсии, а оператор 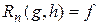оператором примитивной рекурсии.

Если 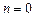, то 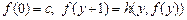. Например, так определяется хорошо знакомая функция факториал.

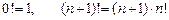
Здесь .

Определение. Функция называется примитивно рекурсивной, если она может быть построена из 0, функци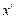й и 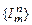с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии.

Примеры.

1) Функция суммы, определяемая равенством 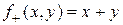, является примитивно рекурсивной, так как она задаётся схемой примитивной рекурсии

,

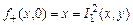
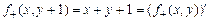т.е. , где 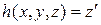, причём функции g и h являются примитивно рекурсивными.

2) Функция арифметического вычитания 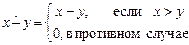. (Проверить самостоятельно).

Арифметизированные логические функции также являются примитивно рекурсивными, так, например, 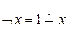. Также с помощью арифметического вычитания можно выразить Ù и Ú (самостоятельно). Из функциональной полноты множества функций следует примитивная рекурсивность всех логических функций.

Определение. Отношение 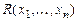называется примитивно рекурсивным, если его характеристическая функция

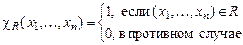
примитивно рекурсивна.

Так как существует взаимно однозначное соответствие между отношениями и предикатами, то 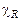будет характеристической функцией и для соответствующего отношению R предиката.

Например, предикат 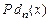делимости нацело числа x на n является примитивно рекурсивным, так как его характеристическая функция 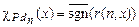, где 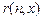– функция, вычисляющая остаток от целочисленного деления x на n, примитивно рекурсивна.

Определение.Оператор называется примитивно рекурсивным, если он сохраняет примитивную рекурсию функций.

Например, условный оператор 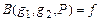, где

,

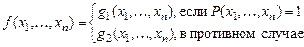является примитивно рекурсивным. Примитивно рекурсивными являются также операторы конечного суммирования и конечного произведения

,

.

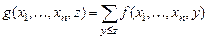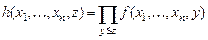Определение. Ограниченный оператор наименьшего числа, называемый ограниченным оператором минимизации (ограниченный m-оператор), определяется равенством

.

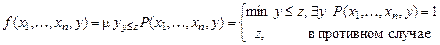Пример. Пусть задан предикат 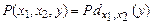, который принимает значение 1, если число y нацело делится на 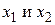. Применение ограниченного оператора минимизации к предикату 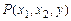имеет результатом функцию .

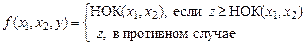Ограниченный оператор минимизации примитивно рекурсивен, он является средством построения обратных функций. Функция 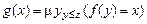является обратной к функции 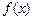. Например, функция целочисленного деления z на x определяется ограниченным оператором минимизации

.

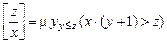В результате рассмотрения примеров функций, которые все являлись примитивно рекурсивными, возникает вопрос: существуют ли не примитивно рекурсивные функции. В данном случае ответ положительный, класс примитивно рекурсивных функций не исчерпывает класс всех вычислимых функций.

Функция Аккермана. Построим функцию, которая является вычислимой, но не примитивно рекурсивной.

Определим последовательность функций 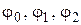по правилу . Функции обладают общими свойствами , ,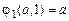

, .

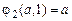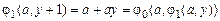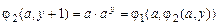Продолжим последовательность по этому рекуррентному правилу

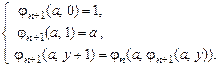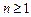( ) (2)

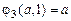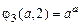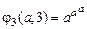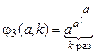Функции примитивно рекурсивны и растут очень быстро. Так, например, , , , ¼ , , ¼

Зафиксируем 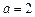и рассмотрим последовательность функций , , ¼ , 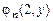, ¼ Определим функцию 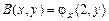, которая обладает свойствами

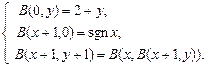(3)

Функция Аккермана определяется как диагональ функции 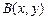, т.е. = .

Функция Аккермана является вычислимой, так как соотношения (2), (3) позволяют построить программу для её вычисления. Однако данная функция не является примитивно рекурсивной, так как она в силу (3) является двукратно рекурсивной. Поэтому средства построения вычислимых функций нуждаются в расширении. Оператор кратной рекурсии не замыкает класс вычислимых функций, так как для любого n можно построить функцию, которая является 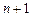-рекурсивной, но не n-рекурсивной. Средством завершающим построение вычислимых функций является m-оператор.

Определение.

Определение. Функция называется частично рекурсивной, если она может быть построена из 0, функци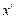й и 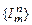с помощью конечного числа применений операторов суперпозиции, примитивной рекурсии и m-оператора.

Частично рекурсивная функция может быть определена не для всех значений. Например, функция обратная к функции следования 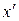, задаваемая равенством 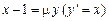, не определена при .

Определение. Частично рекурсивная функция называется общерекурсивной, если она всюду определена.