Полиномиальная сводимость. NP-полные языки и задачи.

Какова связь между определёнными выше классами задач P и NP? Очевидно, что 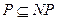(стадия угадывания отсутствует). Естественным кажется предположить, что включение является строгим, однако это утверждение в настоящее время не доказано. Самым сильным доказанным фактом является утверждение

Теорема 4.1. Если 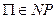, то существует полином 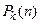, что P может быть решена детерминированным алгоритмом с временной сложностью .

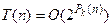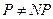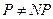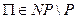Поэтому все утверждения в теории NP-полных задач формулируются, исходя из предположения, что . Цель теории NP-полных задач заключается в доказательстве более слабых результатов вида: «Если , то ». Данный условный подход основывается на понятии полиномиальной сводимости.

Определение. Язык 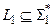полиномиально сводится к языку 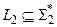, что обозначается 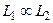, если существует функция 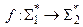, удовлетворяющая условиям:

1) Существует ДМТ-программа M, вычисляющая f с временной сложностью, ограниченной полиномом, т.е. 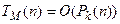при некотором k;

2) Для любого 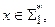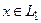в том и только том случае, если .

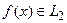Пусть – задачи распознавания, а 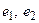– их схемы кодирования, то задача P₁ полиномиально сводится к задаче P₂ (обозначается 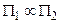), если .

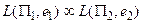Например, задача существования гамильтонова цикла полиномиально сводится к задаче коммивояжера. Для сведения задачи достаточно положить 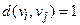, есл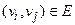и , и 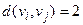, в противном случае. Граница B для длины искомого пути берётся равной 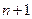, где .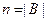

Рассмотрим свойства полиномиальной сводимости.

Лемма 1. Если 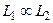, то из 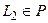следует, что .

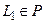Доказательство. Пусть 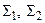– алфавиты языков 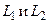соответственно. Так как 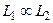, то существует отображение 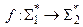. Обозначим через:

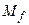– полиномиальную ДМТ-программу, реализующую это отображение;

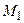– программу распознавания языка ;

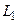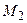– программу распознавания языка .

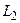Программа распознавания языка 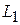может быть построена как композиция программ 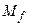и 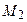. Ко входу 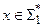применяется программа 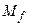, которая строит 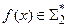, затем к 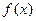применяется программа 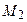, определяющая верно ли, что 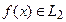. Так как 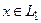Û 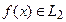, то эта программа является программой распознавания языка .

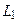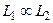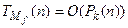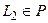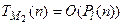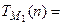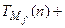
Оценим временную сложность этой программы. Так как , то . Если , то . Тогда = = 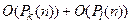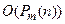, где 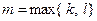. Следовательно, 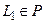. Лемма доказана.

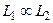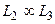Лемма 2. Если и , то .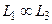

Доказательство аналогично, выполнить самостоятельно.

Определение. Язык L называется NP-полным, если 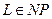и любой другой язык 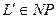полиномиально сводится к L ( ).

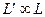Аналогично определяются NP-полные задачи.

Лемма 3. Если 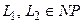, 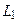является NP-полным и 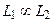, то 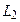является NP-полным.

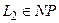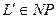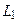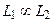Доказательство. Так как , то достаточно показать, что для любого языка справедливо . Язык является NP-полным, а, следовательно, . По условию , поэтому, в силу транзитивности отношения µ (лемма 2) получим .

Лемма 3 даёт рецепт доказательства NP-полноты задачи P, для этого нужно показать, что:

1) ;

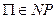2) NP-полная задача 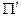полиномиально сводится к P.

Для того чтобы доказывать NP-полноту с помощью полиномиальной сводимости нужно доказать существование хотя бы одной NP-полной задачи. Это сделал в 1971 году С. Кук, а такой задачей явилась задача “выполнимость”.

Задача “выполнимость”.Задано множество логических переменных 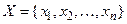и составленный из них набор элементарных дизъюнкций C. Существует ли набор значений множества X, на котором истинны все дизъюнкции множества С?

Эквивалентная формулировка данной задачи: “Является ли выполнимой формула, равная конъюнкции всех элементарных дизъюнкций множества С над множеством высказывательных переменных X?”

Теорема 4.2.(Кука) Задача “выполнимость” является NP-полной.

Рассмотрим основную идею доказательства теоремы. Покажем, что произвольную задачу P из NP можно свести к задаче выполнимость за полиномиальное время.

Так как 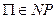, то существует НДМТ-программа M её распознавания с полиномиальным временем работы. Построим группы дизъюнкций, описывающие работу программы M и принимающие значения 1 тогда и только тогда, когда программа M принимает входное слово .

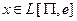Пусть 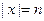, так как 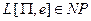, то число шагов МТ-программы ограничивается числом 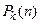, а номера ячеек ограничены интервалом .

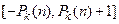Обозначим:

t – момент времени (номер шага программы) ;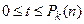

k – номер состояния машины 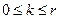, где , ;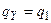

j – номер просматриваемой ячейки ;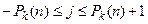

l – номер символа алфавита G 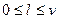, где .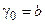

При построении дизъюнкций будут использоваться предикаты:

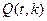– в момент времени t программа находится в состоянии ;

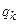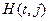– в момент времени t головка просматривает ячейку j;

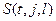– в момент времени t в ячейке j находится символ .

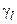При фиксированных значениях предметных переменных они являются высказываниями и могут трактоваться как высказывательные переменные, принимающие различные значения в зависимости от значений параметров.

Выпишем теперь требуемые группы дизъюнкций и оценим количество дизъюнкций в каждой группе.

1. Группа дизъюнкций 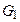описывает конфигурацию программы в начальный момент времени t₀:

a) 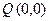– в момент времени 0 программа находится в состоянии q₀;

b) 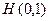– в момент времени 0 головка просматривает 1-ю ячейку;

c) 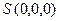– в момент времени 0 в 0-й ячейке находится символ b;

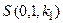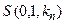d) , , ¼ , – в момент времени 0 в ячейках с номерами с 1-й по n-ю записано входное слово x;

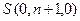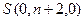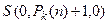e) , , ¼ , – в момент времени 0 ячейки с номерами с n+1 по 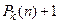пусты.

Общее число этих дизъюнкций равно .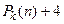

2. Группа 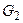содержит утверждения: “В каждый момент t программа M находится только в одном состоянии”. Они записываются следующими дизъюнкциями:

a) , ;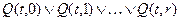

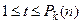b) , .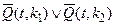

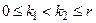Число таких дизъюнкций равно .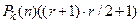

3. Группа 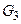содержит утверждения: “В каждый момент t головка просматривает только одну ячейку”. Аналогично 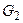получим:

a) , :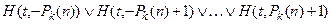

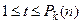b) , .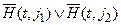

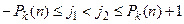Количество дизъюнкций группы равно .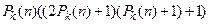

4. Группа 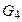содержит утверждения: “В каждый момент t каждая ячейка содержит только один символ алфавита G:

a) , , ;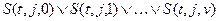

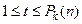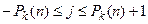b) , .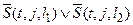

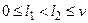Количество дизъюнкций группы равно .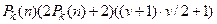

5. Группа 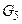описывает переход машинной конфигурации в следующую, согласно функции переходов d ( 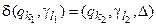). Введём вспомогательную переменную 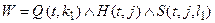, выражающую конфигурацию программы в момент t, где 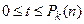, , 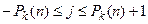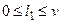. Тогда переход в следующую конфигурацию представляется набором дизъюнкций:

a) 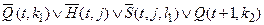(представление в виде ДНФ высказывания );

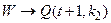b) ( );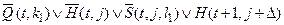

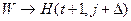c) ( ).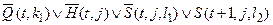

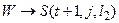Общее число этих дизъюнкций равно .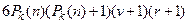

Кроме того, если в момент t ячейка j не просматривается, то её содержимое не меняется. Это описывается высказыванием 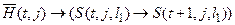, которое эквивалентно дизъюнкции

d) .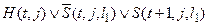

Количество дизъюнкций d) равно .

6. Группа 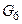, отражающая утверждение “Не позднее, чем через 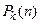шагов программа перейдёт в состояние q_Y”, состоит из единственного высказывания .

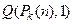Таким образом, если 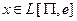, то у программы M есть на входе x принимающее вычисление длины не более 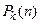, и это вычисление даёт при заданной интерпретации переменных набор значений истинности, который выполняет все дизъюнкции из 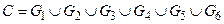. И наоборот, набор дизъюнкций С построен так, что любой выполняющий набор истинности для С должен соответствовать некоторому принимающему вычислению программы M на входе x.

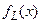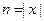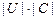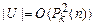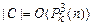Осталось показать, что для любого фиксированного языка L индивидуальная задача “выполнимость” может быть построена за время ограниченное полиномом от . В качестве функции длины для задачи “выполнимость” можно взять . Так как и , то 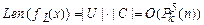. Следовательно, задача “выполнимость” является NP-полной.