В случае плоской задачи. Задача Фламана

Плоская задача согласуется с работой основания ленточных фундаментов, подпорных стен, насыпей и других сооружений, длина которых l не менее чем в 10 раз превосходит их поперечный размер b:

.

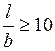В условиях плоской задачи напряжения в грунте определяют исходя из положений, принятых в случае действия сосредоточенной нагрузки, т.е. полагают, что элементарные сосредоточенные силы распределены по линии – линейная нагрузка.

Впервые решение такой задачи для протяженной распределенной нагрузки было дано французским ученым М.Фламаном в 1892г. (рис. 3.6). В каждом сечении, перпендикулярном оси y, распределение напряжений одинаково, т.е. имеет место плоская задача. Составляющие напряжений в произвольной точке основания по этому решению равны

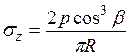; (3.11)

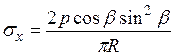; (3.12)

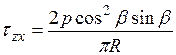. (3.13)

Решение Фламана широко используют для нагрузок, распределенных по полосе. Пусть на поверхность грунта действует нагрузка в виде бесконечной полосы шириной b. Нагрузка изменяется по закону Р = f (x)(рис. 3.7). Распределенную нагрузку на участке dx заменяют сосредоточенной силой dР = Р_x · dx, где 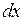– бесконечно малое расстояние по ширине полосы нагружения или по оси x, согласно рис. 3.7 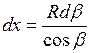. Тогда 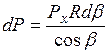. Подставляя значения dР в формулы Фламана (3.11) – (3.13), получим напряжения, вызываемые одним элементом нагрузки. Если нагрузку распространить от значения полярного угла 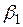до угла 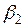, то сумма отдельных элементарных нагрузок дает напряжения в любой точке массива от действия любой полосообразной нагрузки:

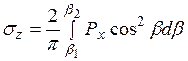, (3.14)

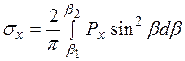, (3.15)

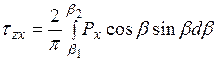. (3.16)

Если полоса загружена не произвольным видом нагрузки, а равномерно распределенной, то результаты интегрирования этих уравнений для P_x = P = const получаются в следующем виде:

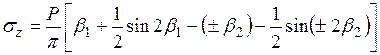; (3.17)

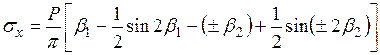; (3.18)

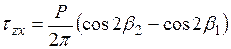. (3.19)

Знак «плюс» перед 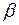принимается для точек, лежащих вне загруженной полосы нагрузки, знак «минус» – для точек в пределах полосы.

Главные напряжения

При равномерно распределенной нагрузке интегрируют выражения (3.14), (3.15) и (3.16) при Р_x = Р = const для точек, лежащих на вертикали под центром полосы симметрии, где 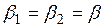. В этом случае главными направлениями, т.е. направлениями, в которых действуют наибольшие и наименьшие нормальные напряжения, будут направления, расположенные по биссектрисе «углов видимости» и им перпендикулярным (рис. 3.8).

Углом видимости называют угол 2β, образованный прямыми, соединяющими рассматриваемую точку М с краями нагрузки.

Подставляя в формулу (3.19) 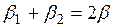, получим 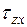= 0. Главные напряжения – напряжения, действующие по главным площадкам.

Главные площадки – площадки, по которым не действуют касательные напряжения. Подставляя в формулы (3.17) и (3.18) значения углов 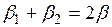, получим формулы главных напряжений в любой точке линейно деформируемого массива под действием равномерно распределенной полосообразной нагрузки.

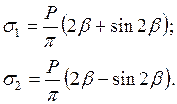(3.20)

Эти формулы используют при оценке напряженного состояния (особенно предельного) в основаниях сооружений.

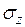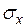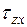По формулам (3.17) – (3.19) можно определить , и в различных точках и построить их эпюры. На рис. 3.9 изображены линии одинаковых вертикальных напряжений 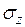, называемых изобарами,горизонтальных напряжений 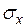, называемых распорами, и касательных напряжений 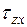, называемых сдвигами.

Изобары показывают, что влияние вертикальных напряжений σ_z интенсивностью 0,1 внешней нагрузки P сказывается на глубине около 6b, тогда как горизонтальные напряжения σ_x и касательные τ_zx распространяются при той же интенсивности 0,1P соответственно на глубину 1,5b и 2,0b.

Влияние ширины загруженной полосы сказывается на глубине распространения напряжений. Например, для фундамента шириной 1 м, передающего на основание нагрузку интенсивностью P, напряжение 0,1P будет на глубине 6 м от подошвы, а для фундамента шириной 2 м при той же интенсивности нагрузки – на глубине 12 м (рис. 3.10).