От сосредоточенной силы
Пространственная задача.Напомним, что распределение напряжений в основании определяется методами теории упругости. Основание при этом рассматривается как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения. Полученные методами теории упругости напряжения соответствуют стабилизированному состоянию, когда все процессы консолидации и ползучести уже завершились и внешняя нагрузка оказывается полностью уравновешенной внутренними силами.
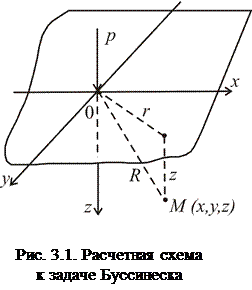 В связи с этим в механике грунтов в основе лежит решение задачи о действии вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства, полученное в 1885 г. Ж.Буссинеском. Это решение
В связи с этим в механике грунтов в основе лежит решение задачи о действии вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства, полученное в 1885 г. Ж.Буссинеском. Это решение
позволяет определить все компоненты напряжений в любой точке полупространства М (x, y, z) от действия силы p (рис. 3.1):
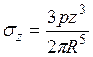 ;
; 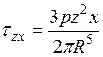 ;
; 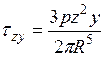 . (3.1)
. (3.1)
Формулам (3.1) можно придать более простой вид, если обозначить
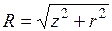 ;
; 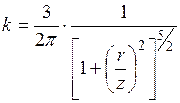 , (3.2)
, (3.2)
 здесь k – коэффициент, зависящий от положения рассматриваемой точки в пространстве. Тогда
здесь k – коэффициент, зависящий от положения рассматриваемой точки в пространстве. Тогда 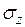 опишется функцией
опишется функцией
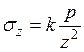 , (3.3)
, (3.3)
в которой коэффициент k определяется по табл. 3.1.
Таблица 3.1
Значения коэффициента k
Отношение 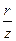
| Коэффициент k | Отношение
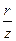
| Коэффициент k | Отношение
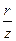
| Коэффициент k |
| 0,00 | 0,4775 | 0,90 | 0,1083 | 1,80 | 0,0129 |
| 0,10 | 0,4657 | 1,00 | 0,0844 | 1,90 | 0,0105 |
Окончание табл. 3.1
| 0,20 | 0,4329 | 1,10 | 0,6580 | 2,00 | 0,0085 |
| 0,30 | 0,3849 | 1,20 | 0,0513 | 2,50 | 0,0034 |
| 0,40 | 0,3294 | 1,30 | 0,0402 | 3,00 | 0,0015 |
| 0,50 | 0,2733 | 1,40 | 0,0317 | 3,50 | 0,0007 |
| 0,60 | 0,2214 | 1,50 | 0,02315 | 4,00 | 0,0004 |
| 0,70 | 0,1762 | 1,60 | 0,0200 | 4,50 | 0,0002 |
| 0,80 | 0,1386 | 1,70 | 0,0160 | 5,00 | 0,0001 |
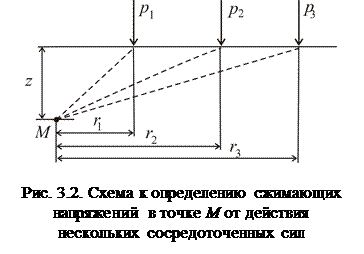
Если на поверхность массива приложено несколько сосредоточенных сил p1, p2, p3, то сжимающее напряжение 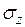 в точке M массива можно определить суммированием напряжений от действия каждой сосредоточенной силы (рис. 3.2):
в точке M массива можно определить суммированием напряжений от действия каждой сосредоточенной силы (рис. 3.2):
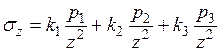 . (3.4)
. (3.4)
 В действительности на основание фундаменты передают не сосредоточенную нагрузку, а сплошную, распределяя ее по некоторой площади. Для определения напряжений в основании можно воспользоваться формулой (3.3), причем существуют два решения такой задачи.
В действительности на основание фундаменты передают не сосредоточенную нагрузку, а сплошную, распределяя ее по некоторой площади. Для определения напряжений в основании можно воспользоваться формулой (3.3), причем существуют два решения такой задачи.
1. Приближенный метод – метод элементарного суммирования. Он состоит в том, что загруженную площадь следует разбить на ряд малых площадок, а нагрузку, действующую на каждую площадку, принять за сосредоточенную силу, приложенную в центре тяжести площадки (рис. 3.3).
Определив величину 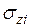 от нагрузки каждой площадки, на которые разбита загруженная площадь, и произведя суммирование этих напряжений, найдем напряжение
от нагрузки каждой площадки, на которые разбита загруженная площадь, и произведя суммирование этих напряжений, найдем напряжение 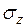 от действия распределенной нагрузки:
от действия распределенной нагрузки:
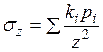 . (3.5)
. (3.5)
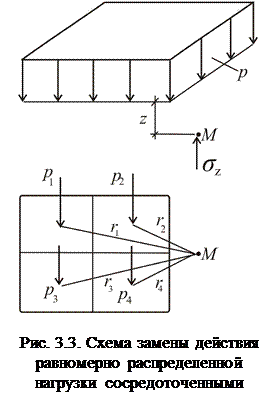 2. Точный метод определения напряжений от распределенной нагрузки состоит в том, что эти напряжения определяются интегрированием выражения (3.1) в пределах контура загружения от нагрузки на бесконечно малый элемент загруженной площади.
2. Точный метод определения напряжений от распределенной нагрузки состоит в том, что эти напряжения определяются интегрированием выражения (3.1) в пределах контура загружения от нагрузки на бесконечно малый элемент загруженной площади.
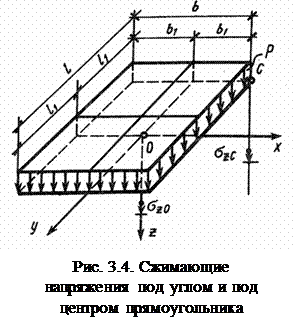
Напряжения в основании от равномерной нагрузки, распределенной по прямоугольнику. Метод угловых точек.Значения сжимающих напряжений 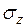 в любой точке основания от действия нагрузки интенсивностью p, равномерно распределенной по площади прямоугольника размером l x b, впервые были получены А.Лявом в 1935г. Практический интерес представляют напряжения для точек, лежащих на вертикали под углом
в любой точке основания от действия нагрузки интенсивностью p, равномерно распределенной по площади прямоугольника размером l x b, впервые были получены А.Лявом в 1935г. Практический интерес представляют напряжения для точек, лежащих на вертикали под углом 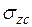 и под центром
и под центром 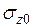 загруженного прямоугольника (рис. 3.4).
загруженного прямоугольника (рис. 3.4).
 |  |
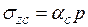 ;
; 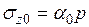 , (3.6)
, (3.6)
где 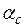 и
и 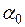 – соответственно табличные коэффициенты влияния для угловых и центральных напряжений, зависящие от отношения сторон прямоугольника
– соответственно табличные коэффициенты влияния для угловых и центральных напряжений, зависящие от отношения сторон прямоугольника 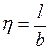 и относительной глубины рассматриваемой точки
и относительной глубины рассматриваемой точки 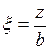 (под углом прямоугольника) и
(под углом прямоугольника) и 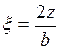 (под центром прямоугольника) (табл. 3.2).
(под центром прямоугольника) (табл. 3.2).
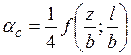 ,
, 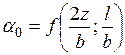 . (3.7)
. (3.7)
Таблица 3.2
Значения коэффициентов 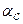 и
и 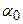
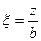
| Прямоугольник с соотношением сторон 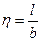 , равным , равным
| |||||
| 1,0 | 1,4 | 1,8 | 3,2 | |||
| 0,0 0,4 0,8 1,2 1,6 2,0 2,4 3,2 4,0 4,8 6,0 7,2 8,4 10,0 12,0 | 1,000 0,960 0,800 0,606 0,449 0,336 0,257 0,160 0,108 0,077 0,051 0,036 0,026 0,019 0,013 | 1,000 0,972 0,848 0,682 0,532 0,414 0,325 0,210 0,145 0,105 0,070 0,049 0,037 0,026 0,018 | 1,000 0,975 0,866 0,717 0,578 0,463 0,374 0,251 0,176 0,130 0,087 0,062 0,046 0,,033 0,023 | 1,000 0,977 0,879 0,749 0,629 0,530 0,449 0,329 0,248 0,192 0,136 0,100 0,077 0,056 0,040 | 1,000 0,977 0,881 0,754 0,639 0,545 0,470 0,360 0,285 0,230 0,173 0,133 0,105 0,079 0,058 | 1,000 0,977 0,881 0,755 0,642 0,550 0,477 0,374 0,306 0,258 0,208 0,175 0,150 0,126 0,106 |
Метод угловых точек. Для определения напряжений в любой точке грунтового полупространства пользуются методом угловых точек. Для этого прямоугольную площадь загружения разбивают на составные прямоугольники таким образом, чтобы точка М, под которой определяют напряжения, оказалась угловой по отношению к вновь образованным прямоугольникам (рис. 3.5). Здесь возможны различные варианты. Точка М находится на контуре, внутри и за пределами площади прямоугольника.

В первом случае имеем
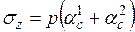 . (3.8)
. (3.8)
Во втором случае имеем
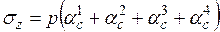 . (3.9)
. (3.9)
В третьем случае имеем
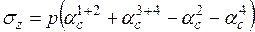 , (3.10)
, (3.10)
где p – интенсивность внешней равномерно распределенной нагрузки; 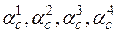 – угловые коэффициенты, определяемые по табл. 3.2 в зависимости от
– угловые коэффициенты, определяемые по табл. 3.2 в зависимости от 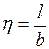 и
и 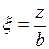 .
.
Метод угловых точек широко используется для определения взаимного влияния фундаментов на деформацию их оснований.
Дата добавления: 2016-01-09; просмотров: 1098;
