Напряжения в основаниях дорожных насыпей
При возведении насыпей нагрузка в их основании может быть сведена к симметричной треугольной нагрузке. В этом случае сжимающее напряжение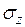 
под центром равнобедренного треугольника (рис. 3.11) определяется по формуле
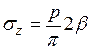, (3.21)
где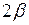 
– угол видимости.
В случае нагружения основания насыпи по закону трапеции напряжения в точке М основания могут быть получены как разность напряжений от двух треугольных нагрузок (рис. 3.12)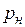 
= p1 – p2. Из подобия треугольников находим p1 и p2:
; 
.
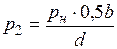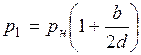Тогда из (3.21) получим
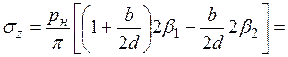
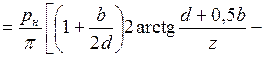
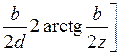. (3.22)
При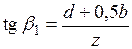 
и
, и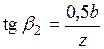спользуя параметры 
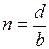и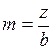 
и подставляя в формулу (3.22), получим
.
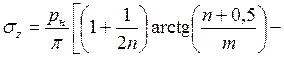
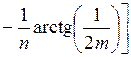Обозначим
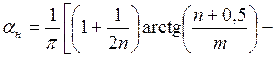
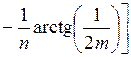– коэффициент рассеивания напряжений, определяемый по табл. 3.3.
Напряжение в основании насыпи по её оси определяется формулой
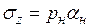, (3.23)
в которой 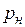– интенсивность нагрузки,
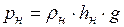, (3.24)
здесь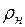 
– плотность грунта тела насыпи; 
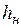– высота насыпи.
Напряжения в произвольной точке основания насыпи.
Метод полунасыпи
В условиях плоской задачи при любой насыпной нагрузке напряжения на глубине z под краем полунасыпи равно половине напряжения на той же глубине по оси полной насыпи. Дополняем полунасыпь до полной насыпи (рис. 3.13).
Полное напряжение
.
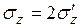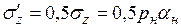. (3.25)
Напряжения в любой точке, не лежащей под центром насыпи, (рис. 3.14, а):
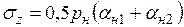; (3.26)
; 
.
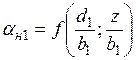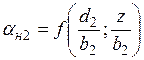а) б)
Определение напряжений в основании для точки, лежащей за пределами насыпи, производят по разности напряжений от двух полунасыпей
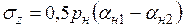, (3.27)
где ; .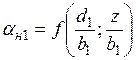
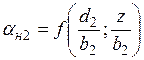Дата добавления: 2016-01-09; просмотров: 1283;