Основные исходные положения

Осадкой называется вертикальное перемещение точек поверхности грунта или подошвы фундамента от внешней нагрузки, т.е. это сжатие грунта, слагающего основание. Полная величина осадки, как уже было рассмотрено выше, состоит из упругой и остаточной частей. В грунтах остаточные деформации играют основную роль, они в большинстве случаев в несколько раз превосходят по величине упругие деформации.

Следует различать абсолютную величину осадки и разность осадок отдельных частей сооружения. Равномерная осадка, даже значительная, не представляет опасности для устойчивости сооружения, в то время как разность осадок может существенно повлиять на работу сооружения. Неравномерные осадки связаны с различными показателями свойств грунтов под разными частями сооружений: неравномерностью давлений на грунт, различием формы и площади фундамента.

Расчет оснований фундаментов базируется на принципе предельного состояния. Расчеты по предельным состояниям подразделяются на две группы:

· I группа - расчеты по несущей способности, направленные на недопущение потери устойчивости сооружения от чрезмерных пластических деформаций;

· II группа - расчеты по деформациям, обеспечивающие установление таких осадок, при которых не произойдет снижение устойчивости сооружения.

Принцип расчетов по I группе предельных состояний заключается в том, что расчетная нагрузка на основание не должна превышать силу предельного сопротивления грунтов основания. По II группе предельных состояний совместная деформация сооружения и основания не должна превышать предельной для конструктивной схемы данного сооружения.

Для промышленного и гражданского строительства расчеты по II группе предельных состояний (по деформациям) являются определяющими (СНиП 2.02.01 - 83^*).

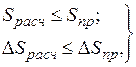(4.1)

т.е. расчётная осадка оснований фундаментов S 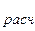и разность осадок соседних фундаментов ∆S 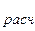должны быть меньше предельных значени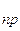й S и ∆S 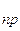, регламентируемых соответствующими нормами и правилами.

Из чего складывается осадка?

1. Из осадки верхнего слоя грунта, нарушенного при подготовке под фундаменты (их можно избежать при качественном ведении работ).

2. Из местных пластических выдавливаний грунта в момент приложения нагрузки (осадки этого рода невелики).

3. Из длительных осадок при уплотнении всей сжимаемой толщи от внешней нагрузки. Если осадки уплотнения окажутся различными для фундаментов в пределах одного и того же сооружения, то нужно проектировать фундаменты так, чтобы разность осадок была меньше предельно допустимой.

Осадка может быть рассчитана, когда известны:

- геологическое строение основания;

- гидрогеологические условия;

- физико-механические свойства грунтов;

- данные о размере и форме фундамента;

- данные о нагрузке на грунт и глубине заложения фундамента.

4.2. Расчёты осадок сооружений

4.2.1. Метод общих упругих деформаций

Этот метод базируется на строгом решении теории упругости для упругого полупространства и для упругого слоя ограниченной конечной толщины, лежащей на несжимаемом основании. Исходным является решение Буссинеска (4.2) для определения вертикальных перемещений точек, расположенных на поверхности полупространства при действии на него сосредоточенной силы (рис. 4.1).

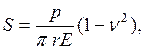(4.2)

При действии на упругое полупространство местной равномерно распределённой нагрузки р по площадке А осадка любой точки определяется путём интегрирования вертикальных перемещений точки от действия элементарной сосредоточенной силы dр (рис. 4.2).

;

; ;

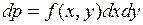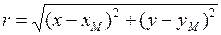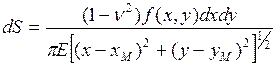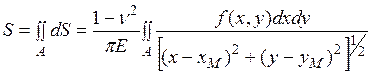. (4.3)

Известно несколько решений этого уравнения для разных очертаний загруженной площади.

Осадка центра круглой площадки при равномерной нагрузке. Вырежем бесконечно тонкую по ширине полоску круга dr (рис. 4.3).

Площадь этой полоски dА = 2πrdr. Элементарная нагрузка dp = p · dA. Осадка от этой нагрузки .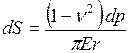

Полная осадка абсолютно гибкой площадки

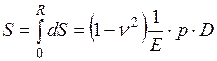. (4.4)

Для абсолютно жесткой площадки

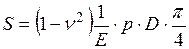. (4.5)

Если прилагать к грунту постоянное давление через жесткие штампы одной формы, но разных размеров, то, как установил Н.А.Цытович, обобщив данные большого числа наблюдений, график зависимости осадки грунтов от размеров площади штампа будет иметь вид, показанный на рис. 4.4. При малых штампах (со стороной менее 0,5 м) развивающиеся под ними пластические деформации приводят к большим осадкам, уменьшающимся с ростом его стороны.

При размерах сторон штампа до 5 ÷ 7 м осадки увеличиваются прямо пропорционально стороне штампа, а при больших размерах они не зависят от величины сооружений, оставаясь практически постоянными и меньшими, чем следует по расчетам, основанным на формулах для однородного линейно деформируемого полупространства. Это связано с неоднородностью грунтового массива, в частности, меньшей сжимаемостью уплотнившихся под действием собственного веса глубинных слоев грунта. По этой причине применение формул теории линейно деформируемых тел для расчета осадок возможно только при небольших площадях фундаментов сооружений и однородных по глубине грунтах.

При больших площадях оснований сооружений или при напластованиях грунтов с разной степенью сжимаемости для вычисления осадок применяют метод послойного суммирования деформаций сжатия слоев в пределах активно сжимаемой толщи грунта.

4.2.2. Осадка слоя грунта при сплошной нагрузке

Рассмотрим сжатие слоя грунта в условиях невозможности бокового расширения при действии на грунт равномерно распределенной нагрузки. Слой безгранично распространен по площади и подстилается несжимаемым скальным основанием. В этом случае сжатие грунта будет происходить аналогично его сжатию в условиях компрессионных испытаний. Из рис. 4.5 видно, что величина осадки

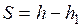, (4.6)

где h – мощность сжимаемого слоя до действия нагрузки; h₁– то же после действия нагрузки.

Величина h₁ может быть найдена из условий постоянства объема минеральных частиц в грунтовой призме площадью А до и после деформации. Объем минеральных частиц в единице объема грунта 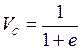. В выделенной грунтовой призме объем минеральных частиц , где А – площадь грунтовой призмы; e₀– коэффициент пористости грунта до приложения нагрузки; e₁– коэффициент пористости после окончания осадки от нагрузки.

Отсюда

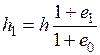. (4.7)

Подставляя выражение (4.7) в формулу (4.6), получим

, (4.8)

тогда согласно компрессионной зависимости

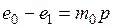, (4.9)

осадка составит 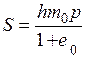. (4.10)

Осадка слоя грунта при сплошной нагрузке пропорциональна мощности слоя h и величине нагрузки p и зависит от коэффициента пористости и коэффициента сжимаемости.

4.2.3. Расчет осадки оснований фундаментов методом

послойного суммирования

Этот метод рекомендован СНиП 2.02.01 - 83^* при расчетах осадок фундаментов оснований. В основу метода положены следующие допущения: осадка основания определяется по вертикальной центральной оси подошвы фундамента; при определении напряжений грунт рассматривается как линейно деформируемое тело (неоднородность основания учитывается при определении деформаций каждого слоя грунта); осадка обуславливается только действием дополнительных вертикальных напряжений 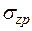; фундаменты не обладают жесткостью; деформации рассматриваются только в пределах сжимаемой толщи H_сж , определяемой условием

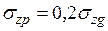, (4.11)

где 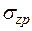– вертикальные дополнительные напряжения; 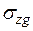– вертикальные природные напряжения (рис. 4.6).

При известных нагрузках от сооружения p определяется среднее давление на основание по подошве фундамента

,

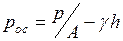где 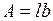– площадь подошвы фундамента; 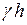– природное давление грунта на уровне подошвы фундамента.

Вследствие постепенного изменения напряжений по глубине основания его толщу можно разбить на ряд слоев так, чтобы в пределах каждого слоя грунт был однородным; при этом толщина каждого слоя должна составлять не более 0,4b и напряжение 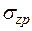вычисляют от нагрузки на границе слоев по формуле

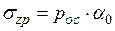, (4.12)

в которой 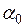определяют по табл. 3.2 и строят эпюру этих напряжений. Затем строят эпюру напряжений природного давления грунта по оси фундамента

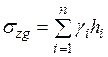, (4.13)

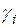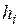здесь и – удельный вес грунта и толщина каждого слоя.

Нижняя граница сжимаемой толщи BC определяется графически путем наложения на эпюру 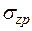эпюры 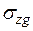, уменьшенной в пять раз.

Общая осадка фундамента определяется путем суммирования в пределах сжимаемой толщи осадок отдельных слоев:

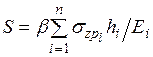, (4.14)

где 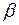= 0,8; n – число слоев в пределах сжимаемой толщи; 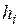– толщина i-го слоя грунта; – модуль деформации i-го слоя грунта.

4.2.4. Осадка грунтового основания во времени

Если в основании фундамента залегают водонасыщенные глинистые грунты, осадка может развиваться в течение длительного времени. Длительный процесс развития осадок связан с очень малой скоростью фильтрации воды в глинистых грунтах (коэффициент фильтрации порядка 10^-7…10^-10 см/с) и медленным уплотнением водонасыщенных грунтов.

Напомним, что к водонасыщенным относятся грунты с коэффициентом водонасыщения 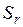> 0,8. Современные методы прогноза развития деформаций грунтов во времени основаны на теории фильтрационной консолидации.

Одномерная задача теории фильтрационной консолидации грунтов, впервые сформулированная проф. К.Терцаги (1924 г.), получила дальнейшее развитие в трудах профессоров Н.М.Герсеванова, В.А.Флорина, Н.А.Цытовича, Ю.К.Зарецкого и др.

В основу теории Терцаги-Герсеванова, разработанной для одномерной задачи консолидации однородного слоя грунта, положены следующие предпосылки и допущения:

1) грунт однородный и полностью водонасыщен;

2) нагрузка прикладывается мгновенно и в первый момент времени полностью передается на воду;

3) скорость осадки грунтового основания определяется скоростью отжатия воды из пор;

4) движение воды в порах грунта происходит в вертикальном направлении и подчиняется закону ламинарной фильтрации Дарси (2.17).

Рассмотрим решение одномерной задачи теории фильтрационной консолидации по Терцаги-Герсеванову, являющейся в настоящее время теоретической основой расчета осадок оснований во времени. Согласно указанным предпосылкам процесс осадок во времени под действием постоянной сплошной равномерно распределенной нагрузки в условиях односторонней фильтрации воды определяется законами фильтрации и уплотнения (2.9).

В начальный момент времени t₀, сразу после приложения нагрузки, внешнее давление р полностью передается на поровую воду 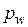, т.е. , а давление на минеральную часть грунта 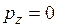. Однако в следующие моменты времени t₁,t₂,…, t_n давление в воде будет уменьшаться, а давление на минеральные частицы грунта увеличиваться, причем в любой момент времени

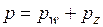(4.15)

и в конце консолидации вся внешняя нагрузка будет восприниматься минеральными частицами грунта ( 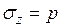) (рис. 4.7).

Слой грунта толщиной h подстилается несжимаемым водонепроницаемым основанием. Нагрузка интенсивностью р воздействует на грунт через дренирующий слой. Следовательно, по мере осадки грунта вода из него будет отжиматься в одном направлении (вверх). По мере отжатия воды из пор грунт будет уплотняться (пористость уменьшаться). Расход воды dq, выдавливаемый из элементарного слоя dz на глубине z (рис. 4.7), будет равен уменьшению пористости грунта dn за промежуток времени dt, т.е.

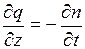. (4.16)

Знак минус указывает, что с увеличением расхода воды происходит уплотнение грунта и его пористость уменьшается. После ряда преобразований, используя законы ламинарной фильтрации и компрессии, уравнение (4.16) можно представить для одномерной задачи в виде дифференциального уравнения в частных производных

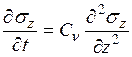, (4.17)

где 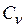– коэффициент консолидации, величина которого зависит от свойств грунта,

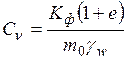, (4.18)

здесь 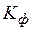– коэффициент фильтрации; 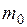– коэффициент сжимаемости грунта; e – коэффициент пористости; 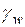– удельный вес воды.

Решение уравнения (4.17) находится путем применения рядов Фурье (т.е. тригонометрических рядов) при следующих краевых условиях:

1) t = 0; 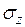= 0;

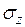2) t = ∞; = р;

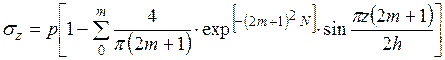, (4.19)

где m – положительное целое число натурального ряда, m = 1,3,5,…, ∞;

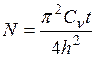– показатель консолидации, (4.20)

h – толщина слоя; t – время от момента загружения.

Если известно напряжение 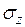в слое dz за время t от момента загружения, то осадка этого слоя следует из выражения (4.10):

.

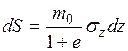Осадку слоя толщиной h за время t найдем, проинтегрировав полученное выражение от 0 до h:

.

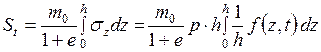В этом выражении часть перед интегралом представляет собой конечную осадку, а часть 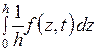может быть определена как степень консолидации осадки U, равная отношению осадок нестабилизированной 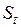к конечной 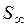, т.е.

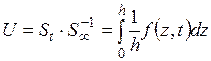. (4.21)

После интегрирования (4.21) получим

.

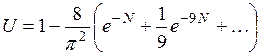Величины U и N функционально связаны. В табл. 4.1 даны величины N для различных вариантов эпюр уплотняющих напряжений (рис. 4.8).

Вариант 0 соответствует уплотнению слоя грунта под действием сплошной нагрузки. Эпюра уплотняющих давлений имеет вид прямоугольника. Вариант 1 имеет место при уплотнении грунта под давлением собственного веса, вариант 2 – когда уплотняющее напряжение уменьшается с глубиной по закону треугольника.

Задаваясь различными значениями степени консолидации U , по табл. 4.1 определяем N и находим время для заданной степени консолидации:

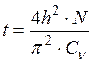. (4.22)

Таблица 4.1

Значения N для определения осадки S_t при различных вариантах эпюр