Аксиома параллельности Лобачевского, основные следствия.

LV₁. (Аксиома параллельности Лобачевского). В любой плоскости существует прямая а₀ и точка А₀, не принадлежащая этой прямой, такие, что через эту точку проходит по крайней мере две прямые, не пересекающие а₀.

Множество точек, прямых и плоскостей, удовлетворяющих аксиомам принадлежности, порядка, конгруэнтности, непрерывности и аксиоме параллельности Лобачевского будем называть трехмерным пространством Лобачевского и обозначать через Л₃. Большинство геометрических свойств фигур будут рассматриваться нами на плоскости пространства Л₃, т.е. на плоскости Лобачевского. Обратим внимание на то, что формальное логическое отрицание аксиомы V₁, аксиомы параллельности евклидовой геометрии, имеет именно ту формулировку, которую мы привели в качестве аксиомы LV₁. На плоскости существует, по крайней мере, одна точка и одна прямая, для которых не выполнено утверждение аксиомы параллельности евклидовой геометрии. Докажем теорему, из которой следует, что утверждение аксиомы параллельности Лобачевского справедливо для любой точки и любой прямой плоскости Лобачевского.

Теорема 13.1.Пусть а – произвольная прямая, А – точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует по крайней мере две прямые, проходящие через А и не пересекающие прямую а.

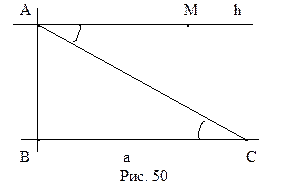Доказательство. Доказательство проведем методом «от противного», при этом воспользуемся теоремой 11.1 (см. § 11). Пусть в пространстве Лобачевского существует такая точка А и прямая а, что в плоскости, определяемой этой точкой и прямой, через точку А проходит единственная прямая, не пересекающая а. Опустим и точки А перпендикуляр АВ на прямую а и в точке А восставим перпендикуляр h к прямой АВ (рис. 50). Как следует из теоремы 4.2 (см § 4) прямые h и а не пересекаются. Прямая h, в силу предположения, - единственная прямая, проходящая через А и не пересекающая а. Выберем на прямой а произвольную точку С. Отложим от луча АС в полуплоскости с границей АВ, не содержащей точку В, угол САМ, равный АСВ. Тогда, как следует из той же теоремы 4.2, прямая АМ не пересекает а. Из нашего предположения следует, что она совпадает с h. Поэтому точка М принадлежит прямой h. Треугольник АВС – прямоугольный, 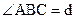. Вычислим сумму углов треугольника АВС: 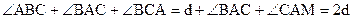. Из теоремы 11.1 следует, что выполнено условие аксиомы параллельности евклидовой геометрии. Поэтому в рассматриваемой плоскости не может существовать таких точки А₀ и прямой а₀, что через эту точку проходит по крайней мере две прямые, не пересекающие а₀. Мы пришли к противоречию с условием аксиомы параллельности Лобачевского. Теорема доказана.

Следует заметить, что в дальнейшем мы будем пользоваться утверждением именно теоремы 13.1, по сути, заменяя им утверждение аксиомы параллельности Лобачевского. Кстати, во многих учебниках именно это утверждение принято в качестве аксиомы параллельности геометрии Лобачевского.

Из теоремы 13.1 легко получить следующее следствие.

Следствие 13.2. В плоскости Лобачевского через точку, не лежащую на данной прямой, проходит бесконечно много прямых, не пересекающих данную.

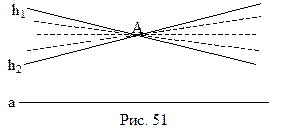Действительно, пусть а данная прямая, а А – точка, ей не принадлежащая, h₁ и h₂ – прямые, проходящие через А и не пересекающие а (рис. 51). Очевидно, что все прямые, которые проходят через точку А и лежат в одном из углов, образованных h₁ и h₂ (см. рис. 51), не пересекают прямую а.

В главе 2 мы доказали ряд утверждений, эквивалентных аксиоме параллельности евклидовой геометрии. Их логические отрицания характеризуют свойства фигур на плоскости Лобачевского.

Во первых, на плоскости Лобачевского справедливо логическое отрицание пятого постулата Евклида. В параграфе 9 нами был сформулирован сам постулат и доказана теорема о его эквивалентности аксиоме параллельности евклидовой геометрии (см. теорему 9.1). Его же логическое отрицание имеет вид:

Утверждение 13.3.На плоскости Лобачевского существуют две непересекающиеся прямые, которые при пересечении с третьей прямой образуют внутренние односторонние углы, сумма которых меньше двух прямых углов.

В § 12 нами было сформулировано предложение Посидония: на плоскости существуют по крайней мере три коллинеарные точки, расположенные в одной полуплоскости от данной прямой и равноудаленные от нее. Также мы доказали теорему 12.6: предложение Посидония эквивалентно утверждению аксиомы параллельности евклидовой геометрии. Таким образом, на плоскости Лобачевского действует отрицание этого утверждения.

Утверждение 13.4. Множество точек, равноудаленных от прямой на плоскости Лобачевского и расположенных в одной полуплоскости относительно ее, в свою очередь не лежат на одной прямой.

На плоскости Лобачевского множество точек, равноудаленных от прямой и принадлежащей одной полуплоскости относительно этой прямой, образуют кривую линию, так называемую эквидистанту. Ее свойства будут рассмотрены нами позже.

Рассмотрим теперь предложение Лежандра: перпендикуляр, проведенный к стороне острого угла в любой точке этой стороны, пересекает вторую сторону угла. Доказанная нами теорема 11.6 (см. § 11) утверждает, что предложение Лежандра эквивалентно аксиоме параллельности евклидовой геометрии. Отсюда следует, на плоскости Лобачевского справедливо логическое отрицание этого предложения.

Утверждение 13.5. На стороне любого острого угла существует такая точка, что перпендикуляр к ней, восставленный в этой точке, не пересекает вторую сторону угла.

Отметим свойства треугольников и четырехугольников плоскости Лобачевского, которые непосредственно следуют из результатов параграфов 9 и 11. Прежде всего, теорема 11.1. утверждает, что предположение о существовании треугольника, сумма углов которого совпадает с суммой двух прямых углов, равносильно аксиоме параллельности евклидовой плоскости. Отсюда и из первой теоремы Лежандра (см. теорему 10.1, § 10) следует следующее утверждение

Утверждение 13.6. На плоскости Лобачевского сумма углов любого треугольника меньше 2d.

Отсюда непосредственно вытекает, что сумма углов любого выпуклого четырехугольника меньше 4d, а сумма углов любого выпуклого n – угольника меньше 2(n-1)d.

Так как на евклидовой плоскости углы, прилежащие к верхнему основанию четырехугольника Саккери равны прямым углам, что в соответствии с теоремой 12.3 (см. § 12) равносильно аксиоме параллельности евклидовой геометрии, то можно сделать следующий вывод.

Утверждение 13.7. Углы, прилегающие к верхнему основанию четырехугольника Саккери – острые.

Нам осталось рассмотреть еще два свойства треугольников на плоскости Лобачевского. Первое из них связано с предложением Валлиса: на плоскости существует хотя бы одна пара треугольников с соответственно равными углами, но не равными сторонами. В параграфе 11 мы доказали, что это предложение эквивалентно аксиоме параллельности евклидовой геометрии (см. теорему 11.5). Логическое отрицание этого утверждения приводит нас к следующему выводу: на плоскости Лобачевского не существует треугольников с равными углами, но не равными сторонами. Таким образом, справедливо следующее предложение.

Утверждение 13.8. (четвертый признак равенства треугольников на плоскости Лобачевского).Любые два треугольника на плоскости Лобачевского, имеющие соответственно равные углы, равны между собой.

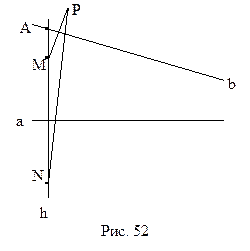Рассмотрим теперь следующий вопрос. Вокруг любого ли треугольника на плоскости Лобачевского можно описать окружность? Ответ на него дает теорема 9.4 (см. § 9). В соответствии с этой теоремой, если вокруг любого треугольника на плоскости можно описать окружность, то на плоскости выполнено условие аксиомы параллельности евклидовой геометрии. Поэтому логическое отрицание утверждения этой теоремы приводит нас к следующему предложению.

Утверждение 13.9. На плоскости Лобачевского существует треугольник, вокруг которого нельзя описать окружность.

Легко построить пример такого треугольника. Выберем некоторую прямую а и точку А, которая ей не принадлежит. Опустим из точки А перпендикуляр h на прямую а. В силу аксиомы параллельности Лобачевского существует прямая b, проходящая через А и не перпендикулярная h, которая не пересекает а (рис. 52). Как известно, если вокруг треугольника описана окружность, то ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника. Поэтому нам достаточно привести пример такого треугольника, серединные перпендикуляры которого не пересекаются. Выберем точку М на прямой h, так как показано на рисунке 52. Симметрично отобразим ее относительно прямых а и b, получим точки N и P. Так как прямая b не перпендикулярна h, то точка Р не принадлежит h. Поэтому точки M, N и P составляют вершины треугольника. Прямые а и b служат по построению его серединными перпендикулярами. Они же, как было сказано выше, не пересекаются. Треугольник MNP – искомый.

Легко построить пример треугольника плоскости Лобачевского, вокруг которого можно описать окружность. Для этого достаточно взять две пересекающиеся прямые, выбрать точку, которая им не принадлежит, и отразить ее относительно этих прямых. Проведите подробное построение самостоятельно.

Определение 14.1. Пусть даны две направленные прямые и . Они называются параллельными, если выполнены условия:

1. 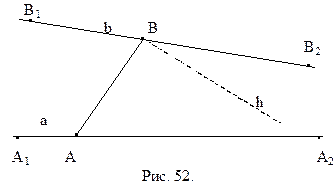прямые а и b не пересекаются;

2. для произвольных точек А и В прямых а и b любой внутренний луч h угла АВB₂ пересекает прямую а (рис. 52).

Обозначать параллельные прямые будем так же, как принято в школьном курсе геометрии: a || b. Заметим, что этому определению удовлетворяют параллельные прямые на евклидовой плоскости.

Теорема 14.3. Пусть на плоскости Лобачевского дана направленная прямая и точка В, которая ей не принадлежит. Тогда через данную точку проходит единственная направленная прямая 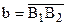такая, что прямая а параллельна прямой b.

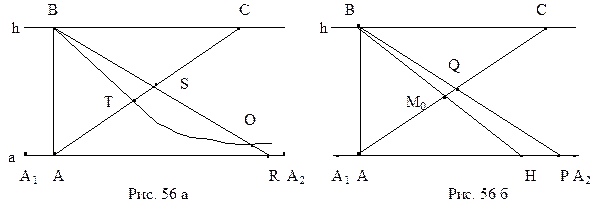Доказательство.Опустим из точки В перпендикуляр ВА на прямую а и из точки В восставим перпендикуляр р к прямой ВА (рис. 56 а). Прямая р, как уже неоднократно отмечалось, не пересекает данную прямую а. Выберем на ней произвольную точку С, разобьем точки отрезка АС на два класса 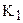и 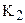. Первому классу 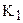будут принадлежать такие точки S этого отрезка, для которых луч BS пересекает луч АА₂, а второму классу 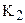принадлежат такие точки T, для которых луч ВТ не пересекает луч АА₂. Покажем, что такое разбиение на классы производит дедекиндово сечение отрезка АС. В соответствии с теоремой 4.3 (см. § 4) нам следует проверить, что:

1. Æ;

2. 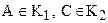и классы 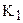и 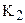содержат точки, отличные от А и С;

3. любая точка класса 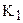, отличная от А, лежит между точкой А и любой точкой класса .

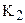Первое условие очевидно, все точки отрезка принадлежат одному или другому классу, при этом сами классы, исходя из их определения, не имеют общих точек.

Второе условие также легко проверить. Очевидно, что 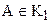и 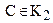. Класс 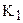содержит точки, отличные от А, для проверки этого утверждения достаточно выбрать какую либо точку луча АА₂ и соединить ее с точкой В. Этот луч пересечет отрезок ВС в точке первого класса. Класс 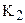также содержит точки, отличные от С, иначе мы придем к противоречию с аксиомой параллельности Лобачевского.

Докажем третье условие. Пусть существует такая точка S первого класса, отличная от А, и такая точка Т второго класса, что точка Т лежит между А и S (см. рис 56 а). Так как 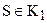, то луч BS пересекает луч АА₂ в некоторой точке R. Рассмотрим луч ВТ. Он пересекает сторону AS треугольника ASR в точке Т. В соответствии с аксиомой 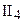Паша этот луч должен пересечь либо сторону AR, либо сторону SR этого треугольника. Предположим, что луч ВТ пересекает сторону SR в некоторой точке О. Тогда через точки В и О проходит две различные прямые ВТ и BR, что противоречит аксиоме 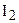аксиоматики Гильберта. Таким образом, луч ВТ пересекает сторону AR, откуда следует, что точка Т не принадлежит классу К₂. Полученное противоречие приводит к утверждению, точка S лежит между А и Т. Условие теоремы 4.3 проверено полностью.

В соответствии с заключением теоремы 4.3 о дедекиндовом сечении на отрезке АС существует такая точка 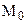, для которой любая точка, лежащая между А и 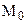принадлежит классу 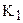, а любая точка, лежащая между 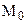и С - принадлежит классу 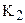. Покажем, что направленная прямая 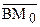параллельна прямой 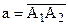. По сути, нам осталось доказать, что 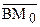не пересекает прямую а, так как в силу выбора точек класса К₁ любой внутренний луч угла 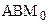пересекает 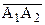. Предположим, что прямая 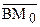пересекает прямую а в некоторой точке Н (рис 56 б). Выберем произвольную точку Р на луче НА₂ и рассмотрим луч ВР. Тогда он пересекает отрезок М₀С в некоторой точке Q (докажите это утверждение самостоятельно). Но внутренние точки отрезка М₀С принадлежат второму классу, луч ВР не может иметь общих точек с прямой а. Таким образом, наше предположение о пересечении прямых ВМ₀ и а неверно.

Легко проверить, что прямая 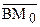единственная направленная прямая, проходящая через точку В и параллельная 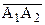. Действительно, пусть через точку В проходит еще одна направленная прямая 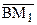, которая, как и 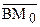, параллельна 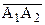. При этом будем считать, что М₁ – точка отрезка АС. Тогда, исходя из определения класса К₂, 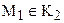. Поэтому, луч ВМ₀ является внутренним лучом угла 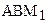, следовательно, в силу определения 14.1 пересекает прямую 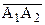. Мы пришли к противоречию с доказанным выше утверждением. Теорема 14.3 доказана полностью.

Рассмотрим точку В и направленную прямую 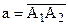, которая ее не содержит. В соответствии с доказанной теоремой 14.3 через точку В проходит направленная прямая 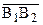, параллельная а. Опустим из точки В перпендикуляр BH на прямую а (рис. 57). Легко видеть, что угол HBB₂ – острый. Действительно, если предположить, что этот угол прямой, то из определения 14.1 следует, что любая прямая, проходящая через точку В пересекает прямую а, что противоречит теореме 13.1, т.е. аксиоме LV₁ параллельности Лобачевского (см. § 13). Легко видеть, что предположение о том, что этот угол тупой, также приводит к противоречию теперь уже с определением 14.1 и теоремой 4.2 (см. §4), так как внутренний луч угла HBB₂, перпендикулярный ВН не пересекает луч АА₂. Таким образом, справедливо следующее утверждение.

Теорема 14.4. Пусть направленная прямая 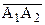параллельна направленной прямой 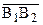. Если из точки В прямой 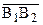опустить перпендикуляр ВН на прямую 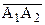, то угол HBB₂ – острый.

Из этой теоремы с очевидностью вытекает следующее следствие.

Следствие. Если существует общий перпендикуляр направленных прямых 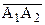и 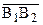, то прямая 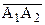не параллельна прямой .

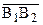Введем понятие параллельности для ненаправленных прямых. Будем считать, что две ненаправленные прямые параллельны, если на них можно выбрать направления так, чтобы они удовлетворяли определению 14.1. Как известно, прямая имеет два направления. Поэтому, из теоремы 14.3 следует, что через точку В, не принадлежащей прямой а проходит две ненаправленные прямые, параллельные данной прямой. Очевидно, они симметричны относительно перпендикуляра, опущенного из точки В на прямую а. Эти две прямые и являются теми самыми пограничными прямыми, разделяющими пучок прямых, проходящих через точку В и пересекающих а, от пучка прямых, проходящих через В и не пересекающих прямую а (рис. 57).

Теорема 15.2. (Свойство симметричности параллельных прямых на плоскости Лобачевского).Пусть направленная прямая 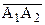параллельна направленной прямой 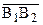. Тогда направленная прямая 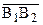параллельна прямой .

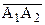Свойство симметричности понятия параллельности прямых на плоскости Лобачевского позволяет нам не указывать порядок направленных параллельных прямых, т.е. не уточнять, какая прямая является первой, а какая второй. Очевидно, что свойство симметричности понятия параллельности прямых имеет место и на евклидовой плоскости. Оно непосредственно следует из определения параллельных прямых в евклидовой геометрии. В евклидовой геометрии выполняется также свойство транзитивности для параллельных прямых. Если прямая а параллельна прямой b, а прямая b параллельна прямой с. то прямые а и с также параллельны между собой. Аналогичное свойство справедливо и для направленных прямых на плоскости Лобачевского.

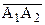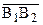
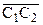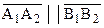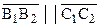Теорема 15.3. (Свойство транзитивности параллельных прямых на плоскости Лобачевского).Пусть даны три различные направленные прямые , . Если и , то .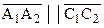

Рассмотрим направленную прямую 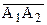, параллельную направленной прямой 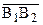. Пересечем их прямой . Точки А и В соответственно точки пересечения прямых 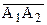, и 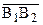, (рис. 60). Справедлива следующая теорема.

Теорема 15.4. Угол 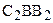больше угла .

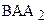Теорема 15.5. Внешний угол вырожденного треугольника больше внутреннего угла, не смежного с ним.

Доказательство непосредственно следует из теоремы 15.4. Проведите его самостоятельно.

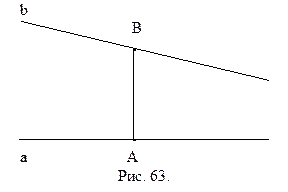Рассмотрим произвольный отрезок АВ. Через точку А проведем прямую а, перпендикулярную к АВ, а через точку В прямую b, параллельную а (рис. 63). Как следует из теоремы 14.4 (см. § 14) прямая bне перпендикулярна прямой АВ.

Определение 16.1. Острый угол, образованный прямыми АВ и b называется углом параллельности отрезка АВ.

Ясно, что каждому отрезку соответствует некоторый угол параллельности. Справедлива следующая теорема.

Теорема 16.2. Равным отрезкам соответствуют равные углы параллельности.

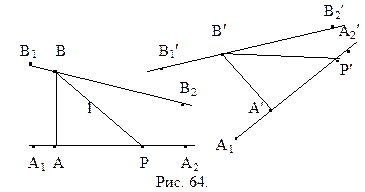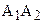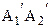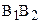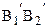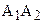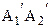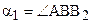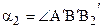Доказательство.Пусть даны два равных отрезкаАВ и А¢В¢. Проведем через точки А и А¢ направленные прямые и , перпендикулярные соответственно АВ и А¢В¢, а через точки В и В¢ направленные прямые и , параллельные соответственно и (рис. 64). Тогда и соответственно углы параллельности отрезков АВ и А¢В¢. Предположим, что

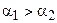. (1)

Отложим от луча ВА в полуплоскости ВАА₂ угол a₂, (см. рис. 64). В силу неравенства (1), луч l – внутренний луч угла АВВ₂. Так как 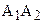½½ 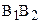, то l пересекает луч АА₂ в некоторой точке Р. Отложим на луче А¢А₂¢ от точки А¢ отрезок А¢Р¢, равный АР. Рассмотрим треугольники АВР и А¢В¢Р¢. Они прямоугольные, по условию теоремы имеют равные катеты АВ и А¢В¢, по построению равны между собой вторая пара катетов АР и А¢Р¢. Таким образом, прямоугольный треугольник АВР равен треугольнику А¢В¢Р¢. Поэтому 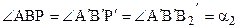. С другой стороны, луч В¢Р¢, пересекает луч А¢А₂¢, а направленная прямая В₁¢В₂¢ параллельна прямой А₁¢А₂¢. Следовательно луч В¢Р¢- внутренний луч угла А¢В¢В₂¢, 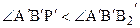. Полученное противоречие опровергает наше предположение, неравенство (1) – ложно. Аналогично доказывается, что угол 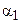не может быть меньше угла 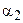. Теорема доказана.

Рассмотрим теперь, как связаны между собой углы параллельности неравных отрезков.

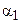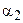Теорема 16.3. Пусть отрезок АВ больше отрезка А¢В¢, а углы и соответственно их углы параллельности. Тогда .

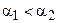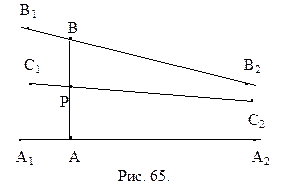Доказательство.Доказательство этой теоремы непосредственно следует из теоремы 15.5 (см. § 15) о внешнем угле вырожденного треугольника. Рассмотри отрезок АВ. Проведем через точку А направленную прямую 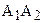, перпендикулярную АВ, а через точку В направленную прямую 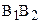, параллельную 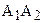(рис. 65). Отложим на луче АВ отрезок АР, равный А¢В¢. Так как 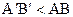, то Р – внутренняя точка отрезка АВ. Проведем через Р направленную прямую С₁С₂, так же параллельную 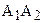. Угол 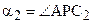служит углом параллельности отрезка А¢В¢, а угол 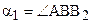- углом параллельности отрезка АВ. С другой стороны, из теоремы 15.2 о симметричности понятия параллельности прямых (см. § 15) следует, что прямая С₁С₂ параллельна прямой 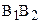. Поэтому треугольник РВС₂А₂ – вырожденный, 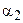- внешний, а 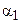- его внутренний углы. Из теоремы 15.5 следует истинность доказываемого утверждения.

Легко доказать обратное утверждение.

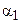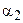Теорема 16.4.Пусть и углы параллельности отрезков АВ и А¢В¢. Тогда, если 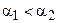, то АВ > А¢В¢.

Доказательство.Предположим противное, 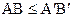. Тогда из теорем 16.2 и 16.3 следует, что 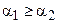, что противоречит условию теоремы.

И так мы доказали, что каждому отрезку соответствует свой угол параллельности, причем большему отрезку соответствует меньший угол параллельности. Рассмотрим утверждение, в котором доказывается, что для любого острого угла существует отрезок, для которого этот угол является углом параллельности. Тем самым будет установлено взаимно однозначное соответствие между отрезками и острыми углами на плоскости Лобачевского.

Теорема 16.5. Для любого острого угла существует отрезок, для которого этот угол является углом параллельности.

Доказательство.Пусть дан острый угол АВС (рис. 66). 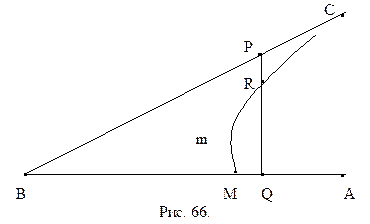Будем считать, что все рассматриваемые в дальнейшем точки на лучах ВА и ВС лежат между точками В и А и В и С. Назовем луч допустимым, если его начало принадлежит стороне угла ВА, он перпендикулярен прямой ВА и расположен в той же полуплоскости относительно прямой ВА, что и сторона ВС данного угла. Обратимся к предложению Лежандра: перпендикуляр, проведенный к стороне острого угла в любой точке этой стороны, пересекает вторую сторону угла. Нами была доказана теорема 11.6 (см. § 11), в которой утверждается, что предложение Лежандра эквивалентно аксиоме параллельности евклидовой геометрии. Отсюда мы сделали вывод, что на плоскости Лобачевского справедливо логическое отрицание этого утверждения, а именно, на стороне любого острого угла существует такая точка, что перпендикуляр к ней, восставленный в этой точке, не пересекает вторую сторону угла (см. § 13). Таким образом, существует такой допустимый луч m с началом в точке М, который не пересекает сторону ВС данного угла (см. рис. 66).

Разобьем точки отрезка ВМ на два класса. Классу 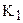будут принадлежать те точки этого отрезка, для которых допустимые лучи с началами в этих точках пересекают сторону ВС данного угла, а классу 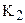принадлежат те точки отрезка ВС, для которых допустимые лучи с началами в этих точках сторону ВС не пересекают. Покажем, что такое разбиение отрезка ВМ образует дедекиндово сечение (см. теорему 4.3, § 4). Для этого следует проверить, что

4. 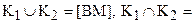Æ;

5. 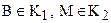и классы 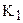и 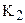содержат точки, отличные от В и М;

6. любая точка класса 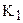, отличная от В, лежит между точкой В и любой точкой класса .

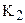Первое условие с очевидностью выполняется. Любая точка отрезка ВМ принадлежит либо классу К₁, либо классу К₂. При этом точка, в силу определения этих классов, не может принадлежать двум классам одновременно. Очевидно, можно считать, что 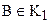, точка М принадлежит К₂, так как допустимый луч с началом в точке М не пересекает ВС. Класс К₁ содержит по крайней мере одну точку, отличную от В. Для ее построения достаточно выбрать произвольную точку P на стороне ВС и опустить из нее перпендикуляр PQ на луч ВА. Если предположить, что точка Q лежит между точками М и А, то тогда точки Р и Q лежат в различных полуплоскостях относительно прямой, содержащей луч m (см. рис. 66). Поэтому отрезок РQ пересекает луч m в некоторой точке R. Мы получим, что из точки R на прямую ВА опущено два перпендикуляра, что противоречит теореме 4.2 (см. § 4). Таким образом, точка Q принадлежит отрезку ВМ, класс К₁ содержит точки, отличные от В. Легко объяснить, почему на луче ВА существует отрезок, содержащий по крайней мере одну точку, принадлежащую классу К₂ и отличную от его конца. Действительно, если класс К₂ рассматриваемого отрезка ВМ содержит единственную точку М, то тогда выберем произвольную точку М¢ между М и А. Рассмотрим допустимый луч m¢ с началом в точке М¢. Он не пересекает луч m, иначе из точки опущены два перпендикуляра на прямую АВ, поэтому m¢ не пересекает луч ВС. Отрезок ВМ¢ искомый, и все дальнейшие рассуждения следует проводить для отрезка ВМ¢.

Проверим справедливость третьего условия теоремы 4.3. Предположим, что существуют такие точк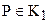и и 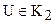, что точка Р лежит между точкой U и М (рис. 67). Проведем допустимые лучи u и p с началами в точках U и P. Так как 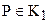, то луч р пересекает сторону ВС данного угла в некоторой точке Q. Прямая, содержащая луч u, пересекает сторону ВР треугольника ВРQ, поэтому согласно аксиоме 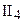аксиоматике Гильберта (аксиома Паша, см. § 3) она пересекает либо сторону ВQ, либо сторону PQ этого треугольника. Но, 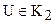, поэтому луч u не пересекает сторону ВQ, следовательно, лучи р и u пересекаются в некоторой точке R. Мы снова пришли к противоречию, так как построили точку, из которой опущены два перпендикуляра на прямую АВ. Условие теоремы 4.3 выполнено полностью.

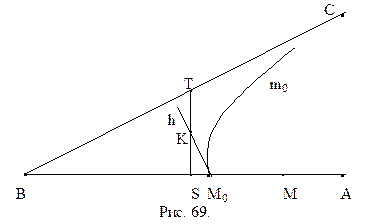
Таким образом, в соответствии с заключением теоремы 4.3, существует такая точка 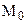отрезка [ВМ], для которой любая точка, лежащая между В и 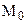принадлежит классу 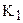, а любая точка, лежащая между 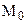и М - классу 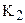. Докажем, что допустимый луч 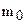с началом в точке 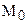параллелен прямой ВС. Для этого, во-первых, докажем, что луч 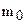не пересекает прямую ВС. Предположим противное, 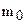пересекает сторону ВС данного угла в некоторой точке Т (рис. 68). Выберем точку S луча ВС, лежащую между Т и С, и опустим из нее перпендикуляр на прямую ВА. Ясно, что основание N этого перпендикуляра будет принадлежать отрезку 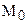М. Отсюда следует, что 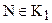. Мы получили противоречие, так как построили точку класса К₁, расположенную между точками 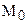и М. Нам осталось показать, что любой внутренний луч угла 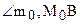пересекает луч ВС. Рассмотрим произвольный внутренний луч h этого угла. Выберем на нем произвольную точку К, принадлежащую углу 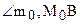, и опустим из нее перпендикуляр на прямую ВА (рис. 69). Основание S этого перпендикуляра, очевидно, принадлежит отрезку ВМ₀, т.е. классу К₁ (докажите этот факт самостоятельно). Отсюда следует, что перпендикуляр KS пересекает сторону ВС данного угла в некоторой точке Т (см. рис. 69). Луч h пересек сторону ST треугольника BST в точке К, согласно аксиоме 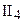(аксиоме Паша), он должен пересечь либо сторону BS, либо сторону ВТ этого треугольника. Ясно, что h не пересекает отрезок BS, иначе через две точки, 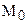и эту точку пересечения, проходят две прямые, h и ВА. Таким образом, h пересекает сторону ВТ, т.е. луч ВА. Теорема доказана полностью.

И так, мы установили, что каждому отрезку в геометрии Лобачевского можно поставить в соответствие острый угол – его угол параллельности. Будем считать, что нами введена мера углов и отрезков, отметим, что мера отрезков будет введена нами позже, в § . Ведем следующее определение.

Определение 16.6. Если под х понимается длина отрезка, а под j - величина угла, то зависимостьj = P(х), ставящая в соответствие длине отрезка величину его угла параллельности, называется функцией Лобачевского.

Ясно, что 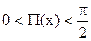. Используя свойства угла параллельности отрезка, доказанные выше (см. теоремы 16.3 и 16.4), можно сделать следующий вывод: функция Лобачевского является монотонно убывающей. Николаем Ивановичем Лобачевским была получена следующая замечательная формула:

,

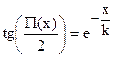где k – некоторое положительное число. Оно имеет важное значение в геометрии пространства Лобачевского, и носит название его радиуса кривизны. Два пространства Лобачевского, имеющие один и тот же радиус кривизны, изометричны. Из приведенной формулы, как нетрудно видеть, также следует, что j = P(х) монотонно убывающая непрерывная функция, значения которой принадлежат интервалу .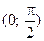

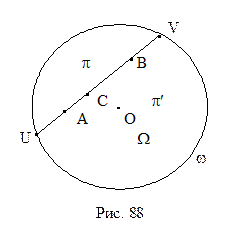На евклидовой плоскости зафиксируем окружность w с центром в некоторой точке O и радиусом, равным единице, которую будем называть абсолютом. Множество всех точек круга, ограниченного окружностью w, обозначим через W¢, а множество всех внутренних точек этого круга - через W. Таким образом, 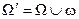. Точки множества W будем называть L‑точками Множество W всех L-точек составляет L-плоскость, на которой мы и будем строить модель Кэли-Кляйна плоскости Лобачевского. Будем называть L‑прямыми произвольные хорды окружности w. Будем считать, что L-точка X принадлежит L‑прямой x тогда и только тогда, когда точка X как точка евклидовой плоскости принадлежит хорде x абсолюта.

L‑плоскости имеет место аксиома параллельности Лобачевского: через L‑точку B, не лежащую на L‑прямой a проходят по крайней мере две L‑прямые b и c, не имеющие общих точек с L‑прямой a. На рисунке 94 приведена иллюстрация этого утверждения. Легко также понять, что из себя представляют параллельные направленные прямые L-плоскости. Рассмотрим рисунок 95. L-прямая b проходит через точку пересечения L-прямой a с абсолютом. Поэтому направленная L-прямая А₁А₂ параллельна направленной L-прямой В₁А₂. Действительно, эти прямые не пересекаются, и, если выбрать произвольные L-точки А и В, принадлежащие соответственно этим прямым, то любой внутренний луч h угла А₂ВА пересекает прямую а. Таким образом, две L-прямые параллельны, если они имеют общую точку пересечения 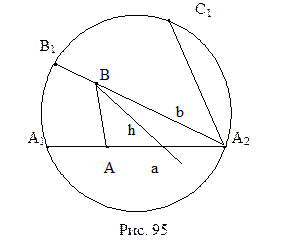с абсолютом. Ясно, что выполняется свойство симметричности и транзитивности понятия параллельности L-прямых. В параграфе 15 свойство симметричности нами было доказано, свойство же транзитивности иллюстрируется на рисунке 95. Прямая А₁А₂ параллельна прямой В₁А₂, они пересекают абсолют в точке А₂. Прямые В₁А₂ и С₁А₂ также параллельны, они также пересекают абсолют в той же точке А₂. Поэтому прямые А₁А₂ и С₁А₂ параллельны между собой.

Таким образом, определенные выше основные понятия удовлетворяют требованиям аксиом I₁-I₃, II, III, IV групп аксиоматики Гильберта и аксиоме параллельности Лобачевского, следовательно являются моделью плоскости Лобачевского. Нами доказана содержательная непротиворечивость планиметрии Лобачевского. Сформулируем это утверждение как следующую теорему.

Теорема 1. Геометрия Лобачевского содержательно непротиворечива.

Мы построили модель плоскости Лобачевского, с построением же пространственной модели, аналогичной рассмотренной на плоскости, можно познакомиться в пособии [4].

Из теоремы 1 следует важнейший вывод. Аксиома параллельности не является следствием аксиом I – IV аксиоматики Гильберта. Так как пятый постулат Евклида равносилен аксиоме параллельности евклидовой геометрии, то этот постулат также не зависит от остальных аксиом Гильберта.