Плоская задача теории предельного равновесия

 Выделим в грунте для плоской задачи элементарную грунтовую призму (рис. 5.1). По двум граням призмы действуют нормальные (
Выделим в грунте для плоской задачи элементарную грунтовую призму (рис. 5.1). По двум граням призмы действуют нормальные ( 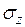 и
и 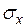 ) и касательные (
) и касательные ( 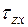 и
и 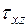 ) напряжения. Третья грань призмы наклонена к горизонтали под углом
) напряжения. Третья грань призмы наклонена к горизонтали под углом 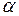 , напряжения на этой грани –
, напряжения на этой грани – 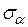 и
и 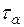 . Угол между полным напряжением р и нормальным
. Угол между полным напряжением р и нормальным 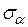 называется углом отклонения
называется углом отклонения 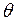 . С изменением угла наклона
. С изменением угла наклона 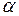 меняется величина нормального и касательного напряжений, меняется угол
меняется величина нормального и касательного напряжений, меняется угол 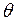 .
.
Рассмотрим предельное напряженное состояние в несвязных грунтах (рис. 5.2). Для той же площадки отложим 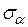 и
и 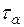 . Точку 1 соединим с началом координат, получим угол
. Точку 1 соединим с началом координат, получим угол 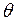 . Устойчивость состояния равновесия характеризуется сравнением величин касательных напряжений
. Устойчивость состояния равновесия характеризуется сравнением величин касательных напряжений 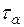 и
и 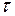 . Если
. Если 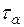 <
< 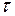 при
при 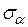 , то это условие устойчивого, т.е. допредельного состояния.
, то это условие устойчивого, т.е. допредельного состояния.
Если касательная составляющая 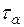 будет возрастать, то она не может быть выше точки 2, т.е. если
будет возрастать, то она не может быть выше точки 2, т.е. если 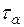 =
= 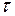 , это предельное равновесие, или иначе предельное состояние, когда угол внутреннего трения равен углу отклонения:
, это предельное равновесие, или иначе предельное состояние, когда угол внутреннего трения равен углу отклонения:
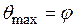 . (5.1)
. (5.1)
Для связных грунтов условие предельного равновесия можно определить путем геометрических построений круга Мора (рис. 5.3).

Откладываем по оси 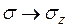 ,затем вверх из точки
,затем вверх из точки 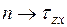 ; откладываем напряжение
; откладываем напряжение 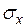 по оси
по оси 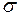 и вниз из точки
и вниз из точки 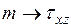 . Точки M и N соединяем прямой. Проводим радиусом aN круг Мора. Откладываем угол
. Точки M и N соединяем прямой. Проводим радиусом aN круг Мора. Откладываем угол 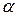 , точку K соединяем с точкой a и проводим касательную в точку K до пересечения с осью
, точку K соединяем с точкой a и проводим касательную в точку K до пересечения с осью 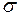 . Получаем два прямоугольных треугольника О1Ka и аNn, в которых Ka = aN.
. Получаем два прямоугольных треугольника О1Ka и аNn, в которых Ka = aN.
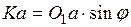 ;
; 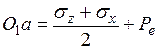 ;
; 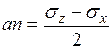 ;
;
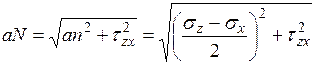 .
.
Так как Ka = aN, отсюда
| |
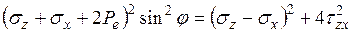 . (5.2)
. (5.2)
Получили условие предельного равновесия в общем виде. Оно связывает напряжения и параметры прочности ( 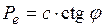 ).
).
В это уравнение входят три неизвестные компоненты напряжений 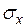 ,
, 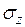 и
и 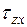 , которые могут быть определены решением системы, состоящей из двух дифференциальных уравнений равновесия и одного алгебраического уравнения – условия предельного равновесия:
, которые могут быть определены решением системы, состоящей из двух дифференциальных уравнений равновесия и одного алгебраического уравнения – условия предельного равновесия:

(5.3)
где x, z – соответственно горизонтальная и вертикальная координатные оси; 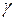 – удельный вес грунта.
– удельный вес грунта.
Условие предельного равновесия можно выразить через главные напряжения, т.к. 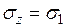 ;
; 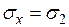 ;
; 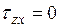 . Подставим их в уравнение (5.2) и получим
. Подставим их в уравнение (5.2) и получим

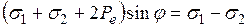 . (5.4)
. (5.4)
Дата добавления: 2016-01-09; просмотров: 1102;
