Напряжения от вертикальной сосредоточенной нагрузки

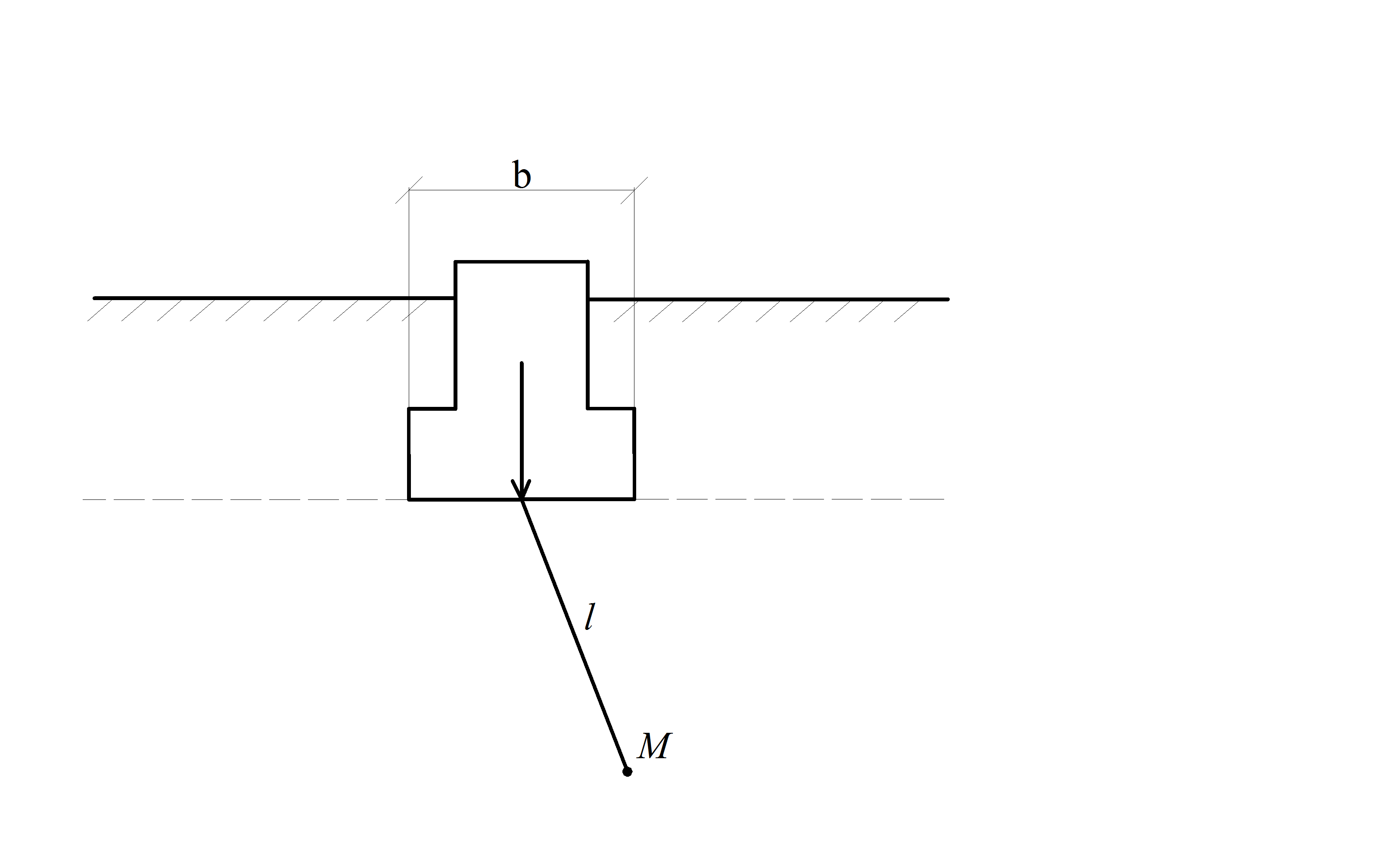
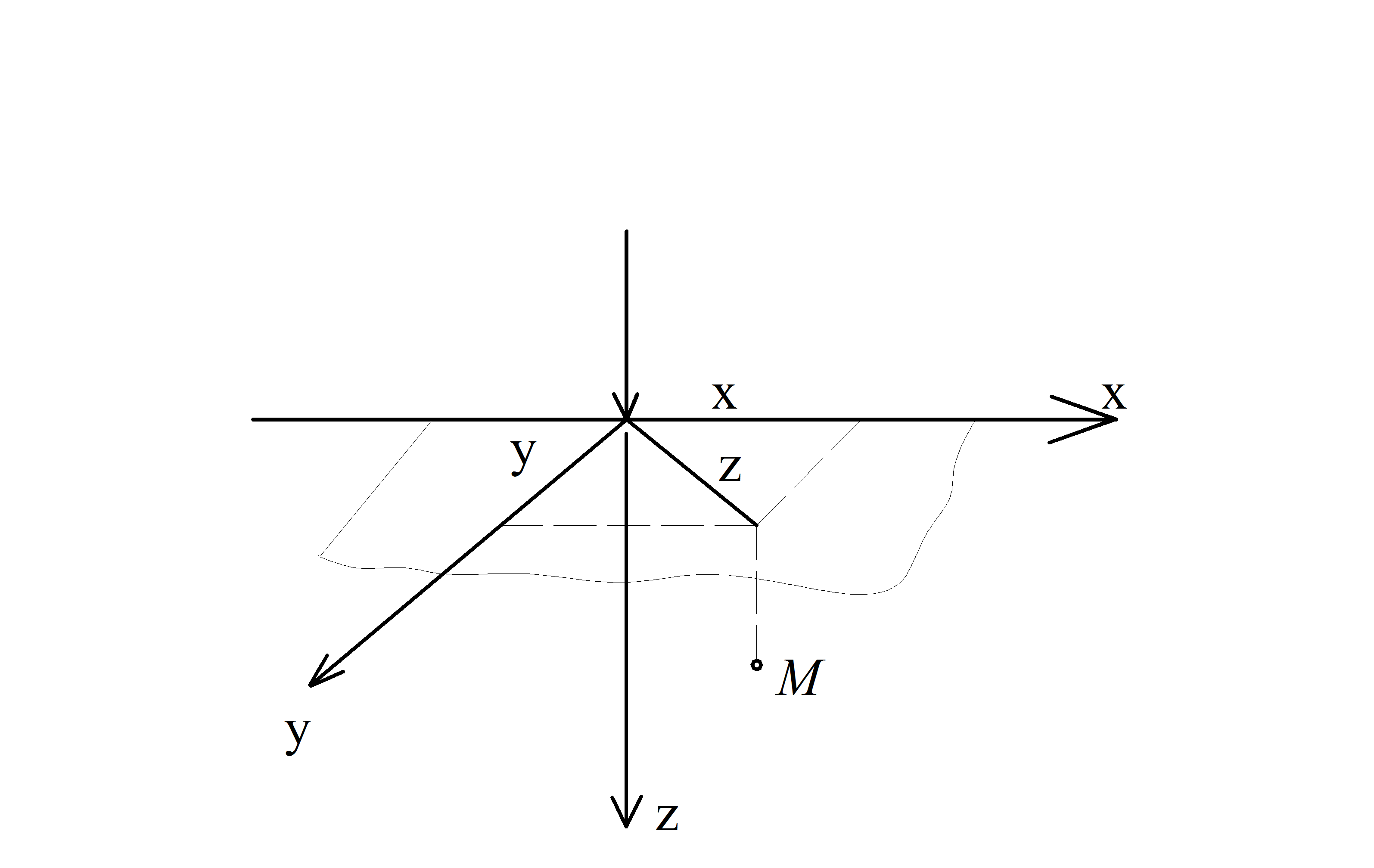
Пусть рассматривается отдельный малозаглубленный фундамент и нужно определить напряжение σ_z в т. М, причем l >b (рис. 3.1, а). Действие фундамента на грунт можно заменить сосредоточенной силой F_v, приложенной в центре подошвы (рис. 3.1,б). Для этой задачи получено решение,

а)	б) FV
эп. σz изобара σz в) FV	г) r3 r2 r1 FV3 FV2 FV1
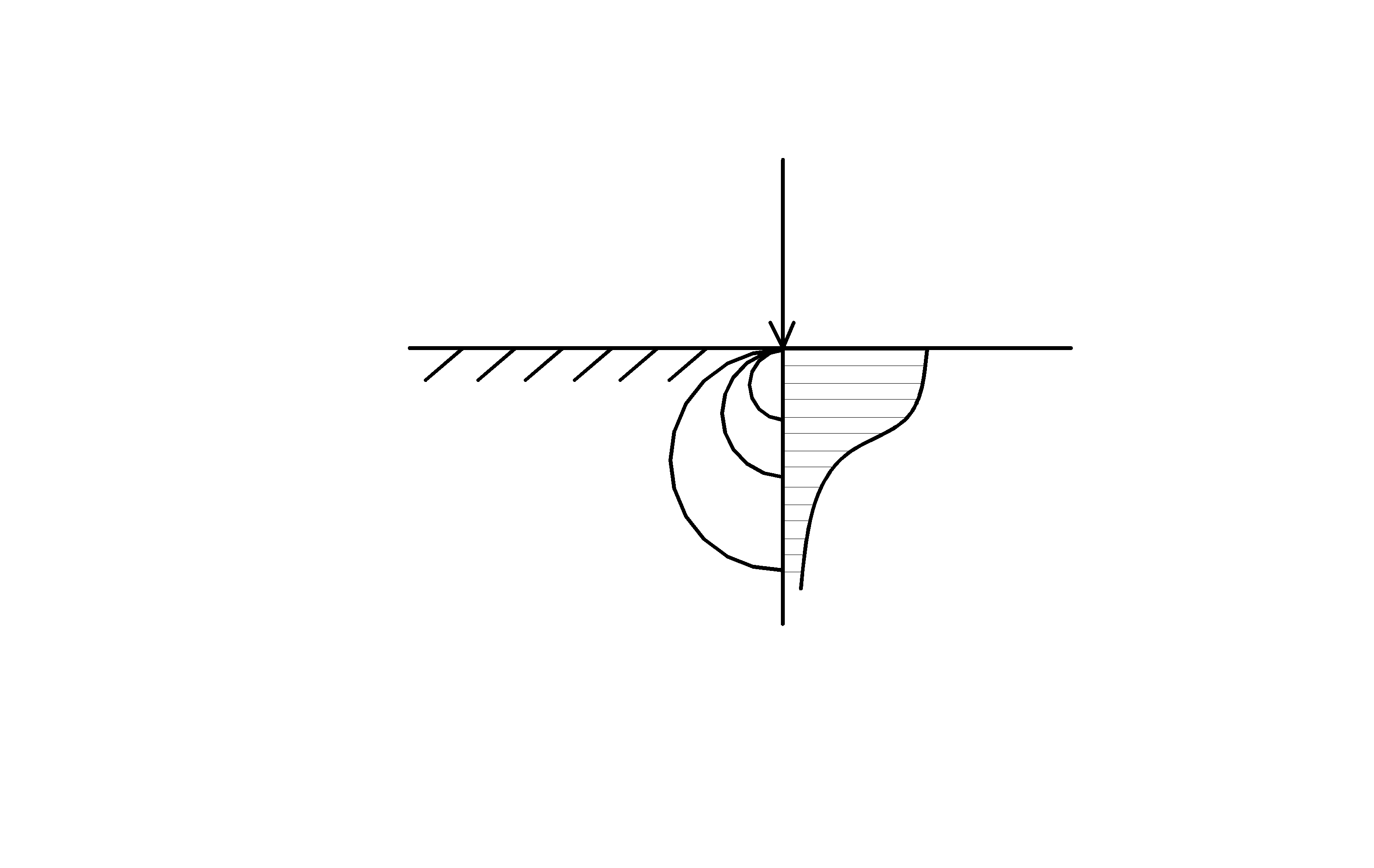
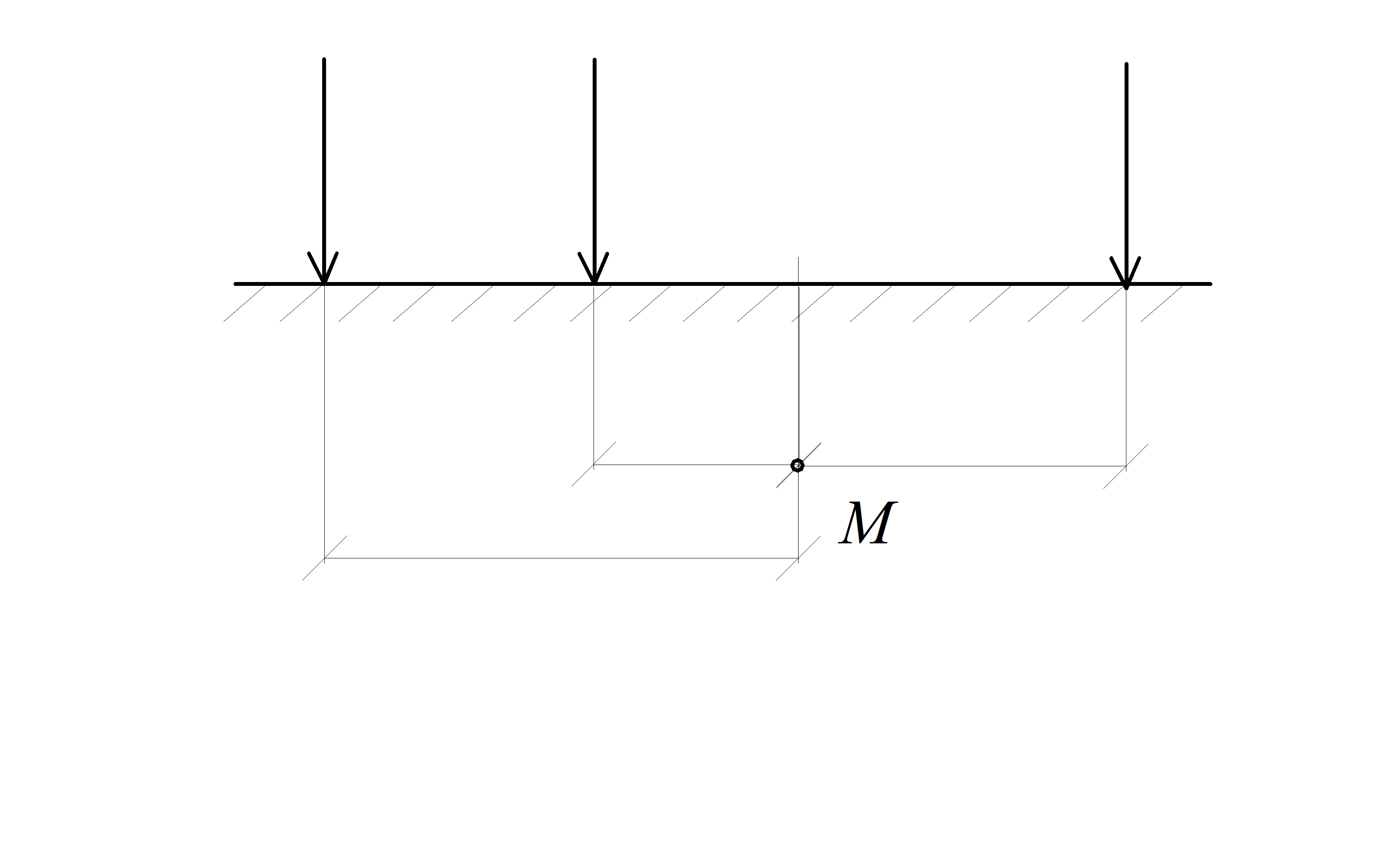
Рис. 3.1

дающее формулы для всех компонент напряжений (Буссинеск, 1885г). Например, для напряжения σ_z:

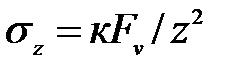(3.1)

где 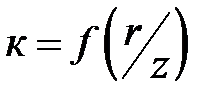- коэффициент влияния, значения которого приведены в табл. 3.1.

Задавшись несколькими значениями z, по (3.1) легко найти напряжения и построить их эпюру, т.е. график изменения по глубине. Другим наглядным способом представления напряженного состояния являются изолинии напряжений (изобары). То и другое показано на рис. 3.1, в.

Таблица 3.1

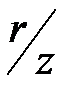
	к		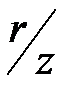к		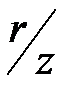к
	0,48	0,6	0,22	1,5	0,025
0,1	0,46	0,7	0,18	1,8	0,02
0,2	0,43	0,8	0,14	2,0	0,009
0,3	0,38	0,9	0,11	2,5	0,003
0,4	0,33	1,0	0,08	3,0	0,0015
0,5	0,27	1,25	0,04	4,0	0,0004

Если необходимо определить напряжение от группы сосредоточенных сил (рис. 3.1, г), рассчитываются и суммируются напряжения от каждой силы (принцип суперпозиции):

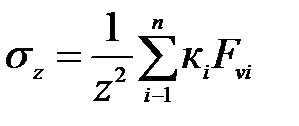(3.2)

Аналогичный прием можно применить для нагрузки, произвольно распределенной на площадке сложной формы. Площадка разбивается на ряд участков и на каждом распределенная нагрузка заменяется сосредоточенной силой. Далее используется (3.2).