Напряжения от полосовой равномерно распределенной нагрузки

Грунт работает в условиях плоской задачи. При этом нормальное напряжение вдоль оси у постоянно, касательные в плоскости xz отсутствуют и напряженное состояние в осях xoz характеризуется тремя компонентами : 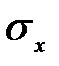, , 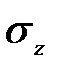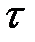. Такое напряженное состояние возникает под ленточными фундаментами стен, насыпями земляного полотна и др. Расчетная схема приведена на рис. 3.3. Требуется определить напряжения в произвольной т. М

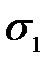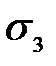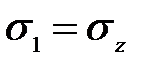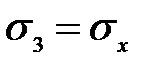Очевидно, что для этого случая можно также использовать формулу (3.3), принимая α по последнему столбцу табл. 3.2. Однако здесь целесообразно привести простые формулы для главных напряжений , . При этом в точках на осевой вертикали в силу симметрии будет и . Главные напряжения равны:

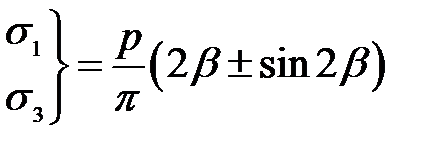, (3.4)

где 2β – угол, под которым видны края полосы из т. М (угол видимости).

Большее напряжение 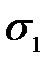направлено по биссектрисе угла видимости, 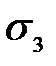– нормально к нему.

Из формулы (3.4) очевиден вид изолиний главных напряжений: это окружности с центром на оси z , проходящие через т. М и края полосы. Во всех точках 2β=const, поскольку угол опирается на одну и ту же хорду – загруженную полосу шириной b. Напряженное состояние в любой точке удобно характеризовать эллипсом напряжений (см. рис. 3.3).

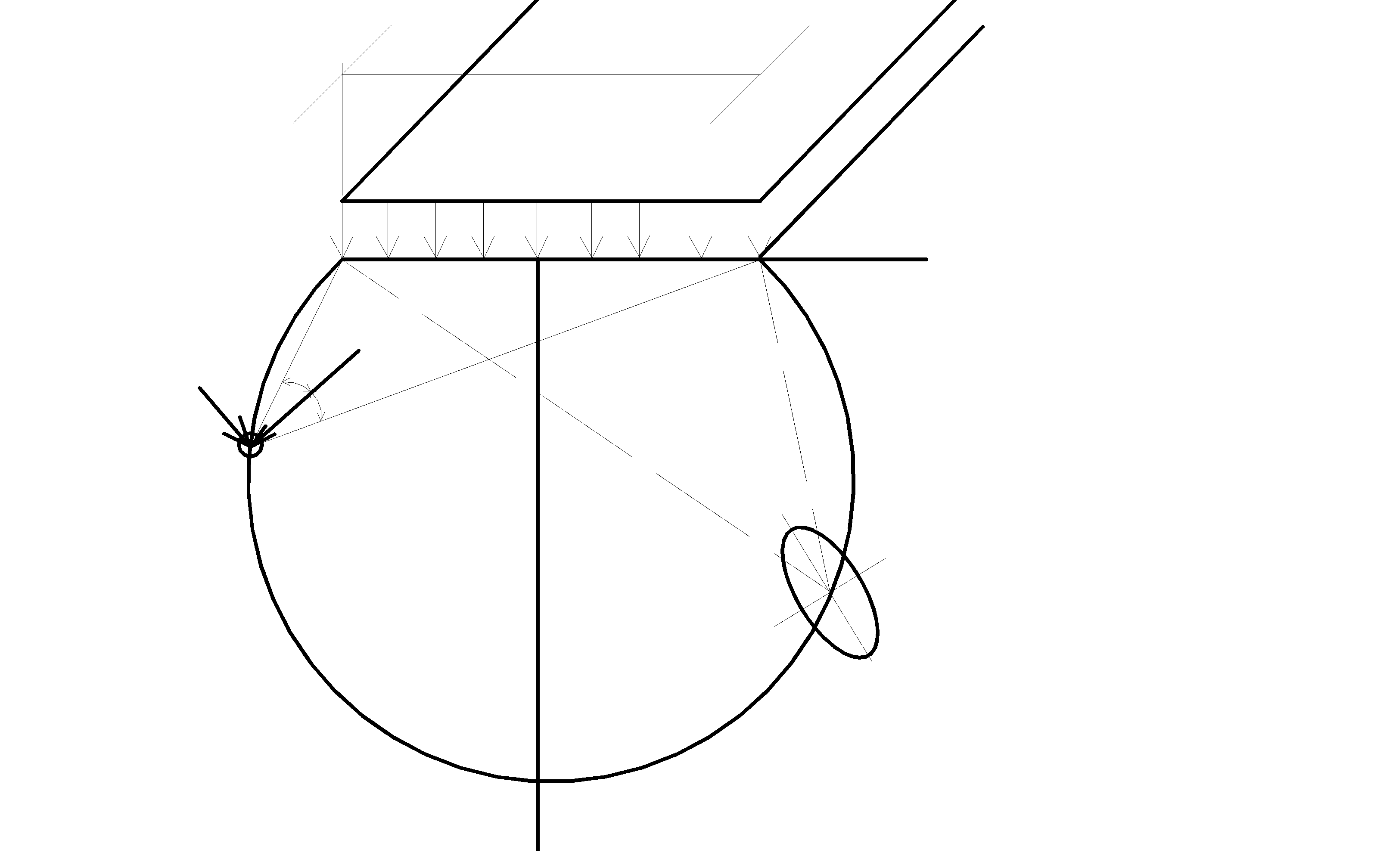
X σ3 σ1 Z σ1 β β M σ3 P l→∞ b   Рис. 3.3 1 – изобара главных напряжений; 2 – эллипс напряжений

Если сравнить изменение напряжений с глубиной от одинаковой нагрузки р, действующей на квадратной или круговой площадке и на полосе той же ширины, то обнаруживается более медленное затухание (убывание) напряжений от полосовой нагрузки (рис. 3.4). Учет этого фактора особенно важен, если на некоторой глубине в основании оказывается прослоек слабого грунта.

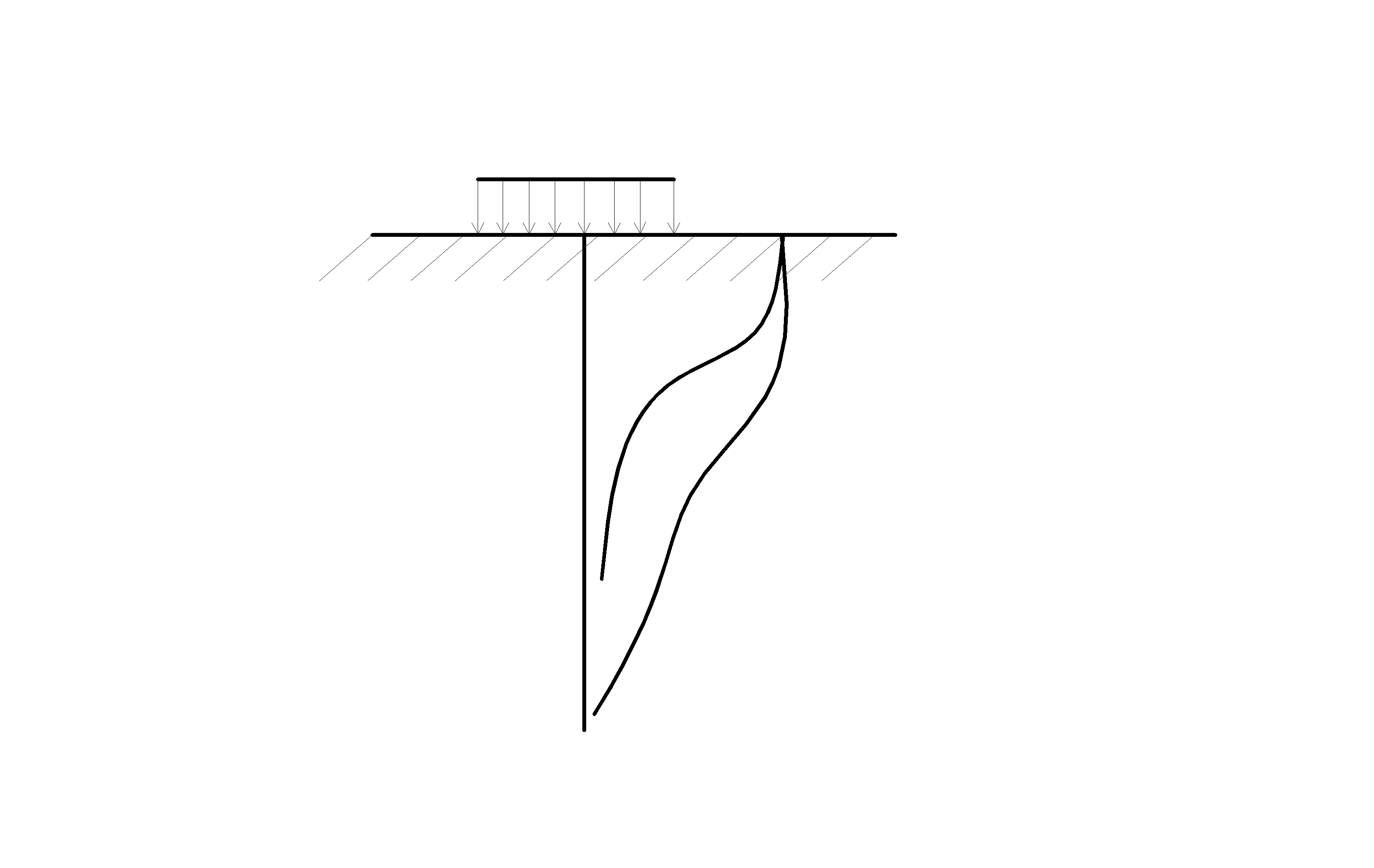
P Рис. 3.4. 1 – нагрузка распределена на квадратной площадке; 2 – то же, на полосе