OCHOBHOЕ УРАВНЕНИЕ УСТАНОВИВШЕГОСЯ РАВНОМЕРНОГО ДВИЖЕНИЯ ЖИДКОСТИ ДЛЯ «ПРАВИЛЬНЫХ РУСЕЛ». РАБОТА СИЛ ВНУТРЕННЕГО ТРЕНИЯ

Обозначим через τ₀ продольное касательное напряжение трения, приложенное со стороны потока жидкости к стенкам русла. «Правильными руслами» принято называть такие русла, для которых или τ₀=const или τ₀≈const вдоль всего смоченного периметра русла (для данного поперечного сечения русла) [1]

Поставим цель найти зависимость потерь напора по длине от величины сил трения в жидкости. Представим на рис. 4-2 часть напорной круглоцилиндрической трубы длиной, равной l, ограниченную сечениями 1 - 1 и 2 - 2. Ось s направим по течению жидкости в трубе. В случае равномерного движения жидкости пьезометрическая линия РР является наклонной прямой (см. § 3-21), причем ее падение на длине l трубы выражает потерю напора h_l.

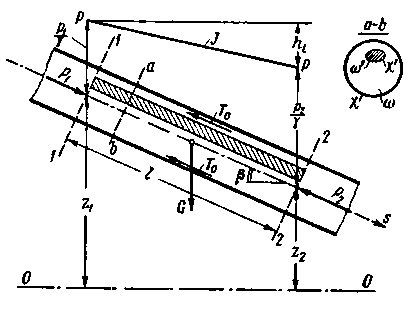
Рис. 4-2. К выводу основного уравнения равномерного движения

Выясним все внешние силы, действующие на рассматриваемую часть потока (расположенную между сечениями 1 - 1 и 2 - 2). После этого, учитывая, что движение жидкости равномерное и установившиеся, сумму проекций найденных сил на ось s приравняем нулю. В результате получим искомое уравнение.

1۫. Силы, действующие на выделенную часть потока. Рассмотрим силы, действующие на эту часть потока.

1. Собственный вес этой части

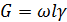, (4-2)
где 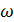- площадь живого сечения потока.

Проекция собственного веса на ось s:

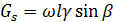, (4-3)
где β – угол наклона оси трубы к горизонту.

Из чертежа видно, что

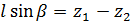; (4-4)

поэтому

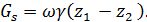(4-5)

2. Силы P₁ и Р₂ давления на торцовые сечения рассматриваемого жидкого отсека со стороны соседних отброшенных объемов жидкости:

(4-6)
где p₁ и р₂ — гидродинамические давления в центрах тяжести живых сечений
1-1 и 2 - 2. Силы Р₁ и Р₂ проектируются на ось s без искажения.

3. Проекция на ось s сил нормального давления на боковую поверхность потока со стороны стенок трубы равняется нулю.

4. Сила «трения на стенке» Т₀, приложенная со стороны стенок трубы к боковой поверхности потока, направлена против течения и проектируется на ось s без искажения. Помимо силы трения на стенке Т₀, являющейся силой внешнего трения, можно различать еще силы внутреннего трения Т. С тем, чтобы пояснить их, представим на рис. 4-3 поперечное сечение рассматриваемой трубы. Изобразим внутри потока две соприкасающиеся струйки a и b: покажем эти струйки в продольном разрезе на рис. 4-3,б (несколько раздвинув их для удобства черчения). В общем случае скорости, отвечающие струйкам а и b, не равны: u_a ≠ u_b. Поэтому струйка а, двигаясь, например, с большей скоростью, стремится увлечь за собой струйку b; при этом к струйке b оказывается приложенной сила трения Т_b, направленная по течению; наоборот, к струйке а со стороны струйки b будет приложена сила внутреннего трения Т_а, направленная против течения.

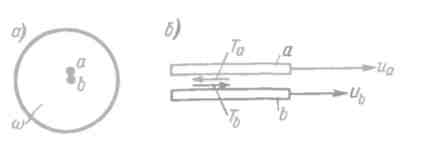
Рис. 4-3. Силы внутреннего трения (их сумма равна нулю; сумма работ этих сил не нулю)

Как видно, силы внутреннего трения являются парными, причем

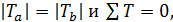
где - внутренние силы трения. Попутно подчеркнем здесь, что сумма работ, описанных выше, равных и противоположно направленных парных сил внутреннего трения Т не равна нулю, поскольку перемещения струек а и Ъ, вызванные этими силами (см. силы Т_а и Т_ь на рис. 4-3) различны (за время dt струйка а вместе с силой Т_а переместится на расстояние u_adt, струйка же b вместе с силой Т_ь — на расстояние u_bdt). Именно эта работа сил внутреннего трения (совместно с работой силы внешнего трения Т₀) и обусловливает потери напора.

2°. Сумма проекций всех сил на ось s.Учитывая сказанное в п. 1°, можем написать:

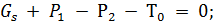(4-7)
подставляя в это уравнение соотношения (4-5) и (4-6), имеем:

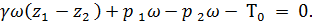(4-8)

Деля выражение (4-8) на 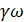, получаем:

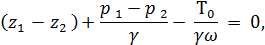
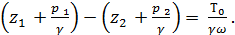(4-9)

Из рис. 4-2 видно, что левая часть (4-9) равна h_l:

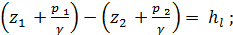(4-10)

поэтому (4-9) переписываем в виде

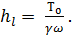(4-11)

где силу Т₀ можно представить (только для «правильных русел» в указанном выше смысле) следующей зависимостью:

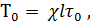(4-12)

причем здесь т₀ - отмеченное выше напряжение трения на стенке (обусловленное трением между жидкостью и стенками трубы) для данного поперечного сечения трубы.

Подставляя (4-12) в (4-11), получаем:

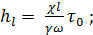(4-13)

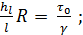(4-14)

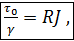(4-15)

где

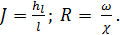(4-16)

Уравнение (4-15) и называется основным уравнением установившегося равномерного движения для «правильных русел».

Из (4-15) или (4-13), учитывая (4-16), получаем для «правильных русел»

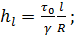(4-17)

именно таким образом для «правильных русел» выражается величина потерь напора h_l, (в случае равномерного движения), обусловленная работой сил внутреннего и внешнего трения.

Как видно, h_l для заданной жидкости и заданных размеров потока зависит только от среднего касательного напряжения трения на стенке .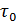

3°.Дополнительые замечания.Рассуждая, как и выше, можно показать, что уравнения (4-15) и (4-17) являются справедливыми не только для напорного движения жидкости в круглоцилиндрической трубе, но и для любого другого случая равномерного установившегося движения; в частности, для случая безнапорного установившегося движения жидкости в цилиндрическом русле любой формы (см. рис. 3-19,6 и 3-29).

Можно показать также, что уравнения (4-15) и (4-17) являются справедливыми и для любого «продольного жидкого столба», выделенного внутри потока (см. например, «жидкий столб», изображенный на рис. 4-2 штриховкой). Для такого «жидкого столба» уравнения (4-15) и (4-17) следует переписать в виде

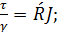(4-18)

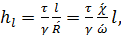(4-19)

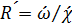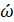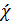где ; и - площадь и смоченный периметр живого сечения этого жидкого столба; τ - касательное напряжение трения для боковой его поверхности, площадь которой равна 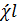; h_l – потеря напора для цельного потока выражаемая формулой (4-10).

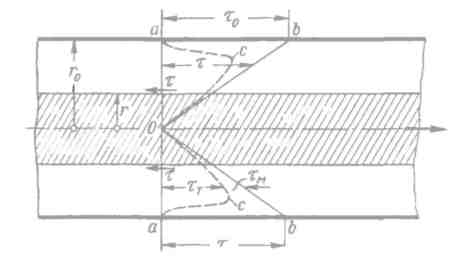
Рис. 4-4. Распределение касательных напряжений продольного трения т по живому сечению потока в круглой напорной трубе (о величинах τ_т и τ_м - см. конец 4-7)

Представим на рис. 4-4 круглоцилиндрическую напорную трубу радиусом r₀ и выделим внутри нее центральный продольный жидкий столб радиусом r (см. чертеж, где этот «столб» заштрихован). Прилагая к нему уравнение (4-18) и учитывая, что в данном случае R' = r/2, можно написать:

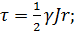(4-20)

отсюда заключаем, что при заданной величине J касательные напряжения τ продольного внутреннего трения для данного живого сечения аа распределяются в круглоцилиндровой трубе вдоль ее радиуса по линейному закону (см. эпюры Oab).