ВЕЛИЧИНА КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ ГРЕНИЯ ПРИ ЛАМИНАРНОМ ДВИЖЕНИИ ЖИДКОСТИ
Представим на продольном разрезе потока (рис. 4-5) некоторое живое сечение АВ и соответствующую ему эпюру скоростей ABC. Покажем далее два слоя жидкости (заштрихованы на чертеже), из которых первый слой движется со скоростью u1 а второй - со скоростью u2. Поверхность соприкосновения 1 - 1 этих жидких слоев имеет площадь S. По этой поверхности (вдоль нее) в реальной (вязкой) жидкости развиваются парные силы внутреннего трения: T1, приложенная к первому слою со стороны второго, и Т2, приложенная ко второму слою со стороны первого. Очевидно,
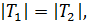 (4-21)
(4-21)
причем первый слой жидкости, движущийся с большей скоростью, за счет трения по поверхности 1 - 1 способствует ускорению движения второго слоя; второй же слой, наоборот, благодаря трению тормозит первый слой.
Рассматривая реальную жидкость, как сплошную среду (в данном случае движущуюся), имеющую касательные напряжения τ, обусловленные существованием сил T1 и Т2 (см. рис. 1-10,а, на котором изображен эллипсоид напряжений, относящийся к общему случаю движения реальной жидкости), мы, естественно, должны иметь ввиду, что силы трения будут возникать не только вдоль поверхности 1 – 1, но и вдоль других направлений, намеченных в точке m (исключение здесь будут составлять только направления главных осей деформаций). В частности, силы трения будут иметь место и в плоскости живого сечения AB.
Мы однако, ограничимся рассмотрением только продольных касательных сил трения, действующих вдоль линий тока, причём будем иметь в виду исключительно прямолинейно параллельноструйный поток жидкости.
Законы продольного внутреннего трения, относящиеся к такому случаю движения, были установлены Ньютоном в 1686 г. Эти законы можно сформулировать так:
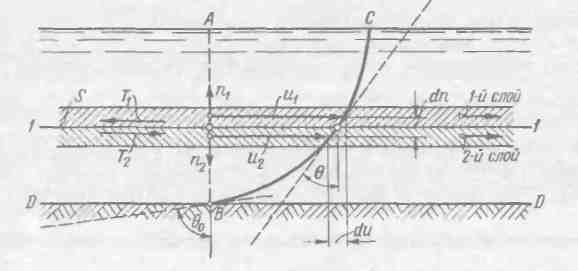
Рис. 4-4. К пояснению законов продольного внутреннего трения в жидкости (для прямолинейного движения)
Сила Т продольного внутреннего трения в параллелъноструйном потоке жидкости, т. е. сила трения, возникающая при скольжении отдельных прямолинейных слоев жидкости, друг по другу[2] (рис. 4-5):
1) прямо пропорциональна так называемому градиенту скорости;
2) прямо пропорциональна площади S поверхности соприкасания данных смев жидкости;
3) не зависит от давления;
4)зависит от физических свойств жидкости (от рода жидкости), а следовательно, и от ее температуры.
Положения 1, 2 и 3 отличаются от соответствующих законов, относящихся к твердым телам: в случае твердых тел сила трения, как известно, зависит от нормального давления и практически не зависит от скорости движения тела, а также от площади S.
Законы Ньютона можно представить в аналитической форме:
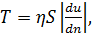 (4-22)
(4-22)
где η — некоторый коэффициент пропорциональности, называемый, как отмечалось выше, динамическим коэффициентом вязкости или просто коэффициентом вязкости[3]. Величина η зависит от рода жидкости, а также от ее температуры; чтобы подчеркнуть это обстоятельство, иногда η называют коэффициентом молекулярной или физической вязкости. Численные значения η для различных жидкостей находятся опытным путем при помощи особых приборов, называемых вискозиметрами; 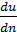 – градиент скорости, т. е. производная от значения скорости |u| по нормали n, проведенной к поверхности 1 - 1 соприкасания слоев жидкости.
– градиент скорости, т. е. производная от значения скорости |u| по нормали n, проведенной к поверхности 1 - 1 соприкасания слоев жидкости.
Если толщина выделенных на рис. 4-5 слоев жидкости бесконечно мала, то для отмеченных на чертеже величин du и dn можем написать:
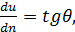 (4-23)
(4-23)
где θ – угол, образованный вертикалью и касательной к кривой ВС эпюры скоростей в точке, лежащей на линии 1 - 1.
Именно соотношением (4-23) и выражается градиент скорости, входящий в формулу (4-22). Величина зависимости от выбранного направления n (см. на рис.4-5 направления n1 и n2) может быть как положительной, так и отрицательной. С тем, чтобы в формуле (4-22) величину Т получать всегда положительной, в эту формулу введено абсолютное значение градиента скорости 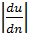 . Впрочем, в дальнейшем для упрощения записей мы будем часто писать в соответствующих случаях просто
. Впрочем, в дальнейшем для упрощения записей мы будем часто писать в соответствующих случаях просто 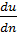 , понимая, однако, под этой величиной абсолютное ее значение.[4]
, понимая, однако, под этой величиной абсолютное ее значение.[4]
Обратим внимание, что при равномерном распределении скоростей поживому сечению, т. е. когда 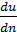 = 0 (что может иметь место в большом удалении от твердой стенки D—D) силы внутреннего трения в реальной (вязкой) жидкости согласно (4-22) должны отсутствовать; при этом вместо эллипсоида напряжений (рис. 1-10, а) мы будем получать для отдельных точек живого сечения шаровые поверхности напряжений (рис. 1-10, б).
= 0 (что может иметь место в большом удалении от твердой стенки D—D) силы внутреннего трения в реальной (вязкой) жидкости согласно (4-22) должны отсутствовать; при этом вместо эллипсоида напряжений (рис. 1-10, а) мы будем получать для отдельных точек живого сечения шаровые поверхности напряжений (рис. 1-10, б).
Касательные напряжения продольного внутреннего трения для ламинарного режима при прямолинейном движении представятся в соответствии с (4-22) зависимостью:[5]
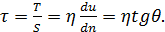 (4-24)
(4-24)
Рассмотрим теперь поверхность дна D - D потока. У самой стенки русла (непосредственно на стенке), как это считает большинство исследователей, имеет место (как для «смачиваемого» материала стенки, так и для «несмачиваемого») скорость u = 0 (для реальной жидкости).[6]
Градиент скорости у стенки равен:
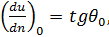 (4-25)
(4-25)
где угол θ0 показан на чертеже.
Имея это в виду, силу Т0 и напряжение τ0 трения на стенке в случае ламинарного режима можно представить зависимостями:
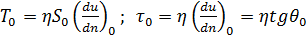 (4-26)
(4-26)
где S0 — площадь смоченной поверхности стенки.[7]
Если в предыдущем параграфе была установлена зависимость τ (или τ0) от величины hl, то в этом параграфе мы установили для ламинарного режима зависимость τ (или τ0) от вязкости жидкости и интенсивности изменения скорости u по живому сечению. Как видно, используя две указанные зависимости, можно через величину τ (или τ0) установить аналитическую связь между потерями напора hl и физическими свойствами жидкости, а также характером распределения скоростей u по живым сечениям потока.
Величины, с которыми сталкивались выше, имеют следующую размерность:
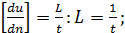 (A)
(A)
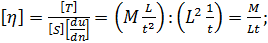 (Б)
(Б)
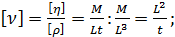 (В)
(В)
где М, L, t — по-прежнему символы массы, длины и времени.
Из (Б) и (В) видно, что ν в отличие от η выражается величинами, не связанными с массой жидкости; в зависимость (В) входят величины, носящие только, так сказать, кинематический характер, в то время как зависимость (Б) носит динамический характер. Именно поэтому η называют динамическим, а
ν - кинематическим коэффициентом вязкости.
В качестве единицы измерения величины η принимают:
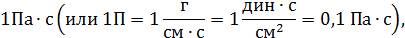
где Па – паскаль, П – так называемый «пуаз», г – грамм массы; в качестве же единицы ν принимают:
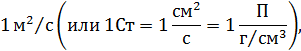
где Ст – так называемый «стокс», г – грамм массы.
Величины η и ν для данной жидкости существенно зависят от температуры. Численные значения этих коэффициентов, найденные опытным путем (при помощи вискозиметров) для некоторых жидкостей, имеющих различную температуру, приводятся в табл. 4-1. Как видно, из этой таблицы, имеем следующие примерные значения η и ν для воды:
а) при температуре ее равной 20°С η ≈ 0,001 Па∙с = 0,01 П;
ν ≈ 10-6 м2/с = 10-2 Ст;
б) при температуре ее равной 10°С η = 0,00131 Па∙с = 0,0131 П;
ν = 1,31∙10-6 м3/с = 1,31∙10-2 Ст.
Таблица 4-1
Коэффициенты вязкости η (в пуазах) и ν (в стоксах) для некоторых жидкостей
| Наименование жидкости | t, °C | η | ν | ||
| Па∙с | П | м2/с | Ст | ||
| 0,001792 | 0,01792 | 1,792∙10-6 | 0,01792 | ||
| 0,001306 | 0,01306 | 1,306∙10-6 | 0,01306 | ||
| 0,001004 | 0.01004 | 1,006∙10-6 | 0,01006 | ||
| Вода | 0,000802 | 0,00802 | 0,805∙10-6 | 0,00805 | |
| 0.000654 | 0,00654 | 0,659∙10-6 | 0,00659 | ||
| 0.000549 | 0,00549 | 0,556∙10-6 | 0,00556 | ||
| Бензин | 0,000650 | 0,00650 | 0.930∙10-6 | 0,00930 | |
| Спирт этиловый | 0,001190 | 0,01190 | 1,540∙10-6 | 0,01540 | |
| Ртуть | 0,001540 | 0,01540 | 0,110∙10-6 | 0.00110 | |
| Скипидар | 0,001600 | 0,01600 | 1,830∙10-6 | 0,01830 | |
| Керосин | 0,002170 | 0,02170 | 2.700∙10-6 | 0,02700 | |
| Глицерин (50%-ный) | 0,006030 | 0,06030 | 5,980∙10-6 | 0,05980 | |
| Масло: | |||||
| трансформаторное | 0,027500 | 0,27500 | 31,000∙10-6 | 0.31000 | |
| веретенное «АУ» | 0,042700 | 0,42700 | 48.000∙10-6 | 0,48000 | |
| турбинное | 0,086000 | 0.86000 | 96,000∙10-6 | 0,96000 |
Дата добавления: 2015-12-29; просмотров: 2440;
