ОСНОВНЫЕ ПОНЯТИЯ, СВЯЗАННЫЕ С ИЗУЧЕНИЕМ ТУРБУЛЕНТНОГО ПОТОКА

1°. Мгновенная местная скорость (актуальная скорость). Структуру турбулентного потока можно себе представить, например, в следующем виде.

При больших скоростях некоторые объемы жидкости (а, b, с; рис. 4-8) разной величины и формы приходят внутри жидкости в беспорядочное не установившееся вращение (получаются водовороты). Множество этих водоворотов, возникающих внутри жидкости и распадающихся на более мелкие изменяется по течению. Имея поступательное движение, они проносятся через данное поперечное сечение потока I - I. Если на этом сечении потока зафиксировать неподвижную точку А, принадлежащую пространству, то через эту точку будут проходить частицы жидкости, имеющие поступательное и вращательное

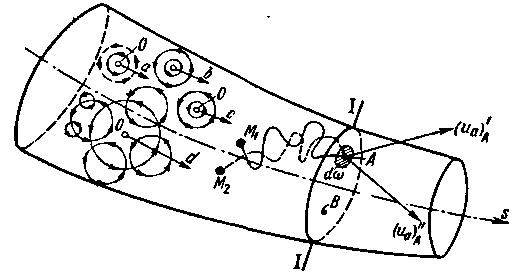
Рис. 4-8. Схема турбулентного движения

движения (относительно перемещающихся центров О); скорость в точке А поэтому все время должна изменяться (и по величине и по направлению)[8]

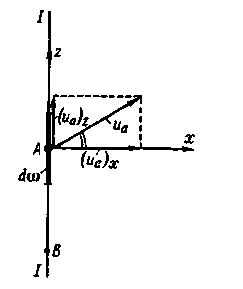
Рис. 4-9. Продольная актуальная скорость [(u_a)_x] и поперечная актуальная скорость [(u_a)_z]

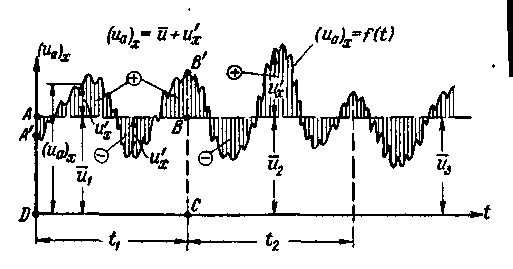
Рис. 4-10. Схема графика пульсаций продольной актуальной скорости для неподвижной точки пространства А (рис. 4-8) u – осредненная продольная скорость

В результате, если в толще потока наметить несколько частиц жидкости (М₁ М₂, ...), попадающих в точку А в разные моменты времени t, то получим следующую картину:

а) частица М₁, двигаясь по некоторой причудливой траектории, попадает в точку А в момент времени t₁ и приобретает в этой точке скорость, которую обозначим через (u_а)'_А;

б) частица М2, двигаясь по другой траектории, попадает в точку А в момент времени t₂ и приобретает в этой точке скорость (u_а)"_А, отличную от скорости (u_а)'_А, и т. д.

В другой точке поперечного сечения I - I, например, в точке В, будем иметь аналогичную картину; для различных моментов времени (t₁ t₂, …) будем получать в этой точке различные скорости: (u_а)'_В; (u_а)''_В; (u_а)'''_В и т.д.

Действительную скорость u_а движения жидкой частицы в данный момент времени в данной точке пространства (например, в точке А или В) называют мгновенной местной скоростью или актуальной скоростью[9]

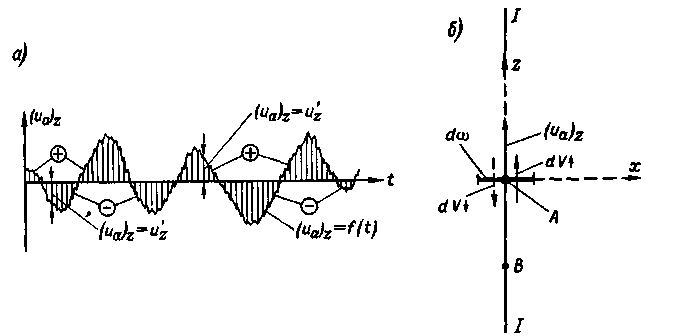
Рис. 4-11. Продольное и поперечное направления турбулентного потока: а — схема графика пульсаций поперечной актуальной скорости для неподвижной точки А пространства; б — поперечный обмен объемами жидкости dV (через площадку dω)

Как видно, актуальная скорость в данной точке пространства изменяется во времени (в общем случае и по величине и по направлению).

2°. Пульсация мгновенной местной (актуальной) скорости.Представим на I рис. 4-9 схему плоского поперечного сечения I - I потока и отметим на нем точку А и элементарную площадку dω, выделенную у этой точки. Проведем к площадке dω нормаль Ах и ортогональ к этой нормали Az; изобразим вектор скорости и_а. Далее спроектируем и_a на направления Ах и Az, причем получим составляющие (и_а)_х и (u_a)_z.[10]

Продольная составляющая актуальной скорости (и_а)_х будет характеризо­ваться следующим:

а) она всегда будет иметь постоянное направление (в отличие от скорости и_а);

б) величина ее будет изменяться во времени (соответственно тому, как
изменяется во времени величина скорости и_а).

Составляющие (и_а)_х и (и_а)_z будем именовать соответственно: мгновенной продольной составляющей скорости (или просто продольной скоростью) и мгновенной поперечной составляющей скорости (или просто поперечной скоростью).

Изменение (и_а)_х во времени в данной точке пространства может быть представлено графиком на рис. 4-10. Этот график, относящийся к определенной точке пространства (например, к точке А), называется графиком пульсации продольной скорости.

Аналогично можно построить график пульсации поперечной скорости (u_a)_z (рис. 4-11,а).

Пульсацией скорости называется явление изменения (увеличение и уменьшение) во времени (т. е. явление флюктуации) величины проекции местной мгновенной (актуальной) скорости на какое-либо направление (например, на линию Ах или на линию Az). С явлением пульсации скоростей иногда сталкиваемся в обыденной жизни; например, наблюдая водоросли, растущие в текущей воде реки, можно заметить, что эти водоросли совершают сложные колебательные движения, которые являются результатом пульсации скоростей; наблюдая уровень воды в трубке Пито, можно видеть, что этот уровень колеблется: то поднимается, то опускается, что также объясняется пульсацией скорости.

3°. Осредненная местная скорость. Пульсационная скорость (пульсационная добавка).Выделим на графике пульсации продольной составляющей скорости (рис. 4-10), относящемся к определенной точке пространства А, доста­точно большой отрезок времени t₁ и затем в пределах этого отрезка осредним величины (и_а)_х: проведем прямую АВ с таким расчетом, чтобы площадь прямоугольника ABCD (Ω_ABCD)равнялась площади фигуры A'B'CD (Ω_A'B'CD) ограниченной кривой графика пульсации:

Ω_ABCD = Ω_A'B'CD

При этом получим некоторое среднее значение u₁, продольной скорости в данной точке А (как здесь, так и ниже, индексы х у осредненных продольных составляющих опускаем).

Выделим далее второй достаточно большой отрезок времени t₂; проведя осреднения продольных мгновенных скоростей в пределах этого отрезка времени, получим некоторое среднее значение 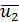продольной скорости в той же, точке А и т. д.

Турбулентное движение жидкости является движением неустановившимся, так как здесь в данной точке пространства актуальные скорости u_a все время изменяются. Вместе с тем, если для данной точки А живого сечения (а также и для других точек этого живого сечения) величины 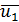, , 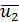, 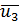…, найденные, как это описано выше, удовлетворяют условиях (рис. 4-10)

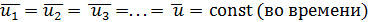(4-47)

то такое турбулентное движение может быть названо в среднем установившимся движением; такого рода движение часто называют просто установившимся, опуская слово «в среднем» (но подразумевая его). Как ясно из сказанного, на рис. 4-10 представлен случай установившегося турбулентного движения. Для неустановившегося турбулентного движения будем иметь 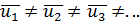Условная (фиктивная) скорость 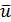называется осредненной местной скоростью; эта скорость является, разумеется, продольной.

Если через dV обозначить объем жидкости, проходящей через элементарную площадку dω (рис. 4-9) за достаточно большой отрезок времени t, то величину осредненной местной скорости при установившемся (в среднем) движении можно представить соотношением

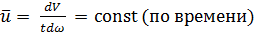(4-48)

Рассматривая рис. 4-10, видим, что продольная актуальная скорость ( 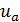)_х может быть представлена в виде:

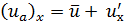, (4-49)

где величина 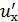(положительная или отрицательная) может быть названа продольной пульсационной скоростью или пульсационной добавкой.

Легко видеть, что для достаточно большого промежутка времени t

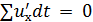(4-50)

поскольку левая часть этого равенства выражается суммой площадей (положительных и отрицательных), показанных на рис. 4-10 штриховкой.

Рассматривая пульсацию поперечных (по отношению к общему направ­лению течения) составляющих актуальной скорости, т. е. пульсацию величин (u_а)_z (рис. 4-11), должны иметь в виду элементарную площадку dω, ортого­нальную оси Oz (рис. 4-11,б). Через эту площадку в связи с наличием скоростей (u_а)_z (изменяющихся во времени как по величине, так и по направлению) будет двигаться жидкость. Обозначим: через dV↑ — объем этой жидкости, прошедшей через площадку dω вверх в продолжении длительного промежутка времени t; через dV↓ — объем жидкости, прошедшей через площадку dω вниз в течение того же отрезка времени t.

Для установившегося (в среднем) турбулентного движения (при достаточно большом t) будем иметь равенство (см. конец настоящего пункта):

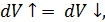(4-51′)

отсюда можем заключить, что объем жидкости dV, прошедший через площадку dω за время t, должен быть равен нулю:

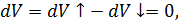(4-51′′)

а следовательно, осредненная поперечная местная скорость

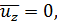(4-52′)

Имея это в виду, можем написать [сообразуясь с аналогичной зависимостью (4-49), в которой мы понимаем под 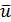величину 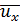], что

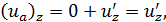(4-52′′)

где и'_z можно назвать поперечной пульсационной скоростью. Как видно, поперечная составляющая актуальной скорости является поперечной пульсационной скоростью. Ясно, что для достаточно большого отрезка времени

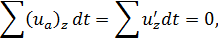
и следовательно, сумма положительных площадей графика пульсации (рис. 4-11, а) равна сумме отрицательных площадей данного графика.

Необходимо в заключение подчеркнуть, что все сказанное выше основан на том предположении, что продольное («главное») и поперечное направления движения жидкости (т. е. направления осей Ах и Az; см. рис. 4-9) были выбраны в начале наших рассуждений с таким расчетом, чтобы соотношение (4-51") было удовлетворено.

4°. Пульсация давлений. Осредненный поток (модель Рейнольдса — Буссинеска). Как показывает опыт, пульсация скоростей сопровождается пульсацией давлений р, т.е. изменением во времени величин р в точках пространства. Рассматривая в среднем установившееся турбулентное движение, можем считать, что для заданной точки пространства (например, точки А на рис. 4-8)

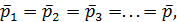(4-53)

где 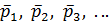— гидродинамические давления, осредненные в точке А за достаточно большие отрезки времени (следующие один за другим) t₁ t₂, t₃, ..; величина 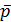может быть названа осредненным местным гидродинамическим давлением.

Для расчета турбулентного потока О. Рейнольде (в 1895 г.) и Ж. Буссинеск (1897 г.) предложили заменять этот поток некоторой воображаемой моделью, представляющей собой условный (фиктивный) поток жидкости, частицы которой движутся со скоростями, равными осредненным местным (продольным) скоростям ( 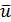), гидродинамические же давления в различных точках пространства, занятого этим потоком, равны осредненным местным давлениям 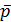. Такой воображаемый поток будем называть осредненным потоком или мо-делью Рейнольдса — Буссинеска. Как видно, поперечные актуальные скорости (u_a)_z при переходе к такой модели исключаются из рассмотрения, т. е. исключается из рассмотрения так называемое «турбулентное перемешивание» (поперечный обмен частицами жидкости между отдельными продольными ее слоями).

Если при движении, называемом нами установившимся, величины 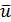в от­дельных точках пространства не изменяются во времени, то при движении, которое мы будем именовать неустановившимся, величины 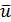должны при рас­смотрении модели Рейнольдса —Буссинеска изменяться во времени.

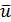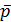Как видно, рассчитывая турбулентный поток согласно Рейнольдсу — Буссинеску, мы должны оперировать величинами и . Поэтому, прилагая, например, уравнение Бернулли к определенному турбулентному потоку, в этом уравнении под величинами и и р всегда следует подразумевать величины 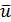и 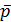; только для упрощения записи в этом случае над буквами и и р не ставят горизонтальных черточек, указывающих на осреднение величин и и р во времени, однако эти черточки всегда подразумевают. Что касается интенсивности пуль­сации скоростей (и_а)_х, то при указанном подходе к вопросу это обстоятельство может быть учтено в уравнении Бернулли величиной корректива α_с (см. ниже п. 6^°).

Действительные линии тока в случае турбулентного потока должны пред­ставлять собой весьма неопределенные кривые, всегда меняющиеся во времени. При рассмотрении же осредненного потока (модели Рейнольдса—Буссинеска) получаем среднестатистические линии (или поверхности) тока (построенные на основе скоростей и) и среднестатистические элементарные струйки, которые не изменяются во времени, если мы имеем установившееся движение (в среднем). Для такого движения указанные среднестатистические поверхности тока должны быть образованы площадками, характеризующимися условием (4-51′).

Надо отметить, что живые сечения осредненного потока, также как и живые сечения действительного ламинарного потока, не являются поверхностями равного напора Н_е. Осредненный поток дает нам вихревое (не потенциальное) движение.

Следует подчеркнуть, что исключаемое из рассмотрения турбулентное перемешивание (при переходе к осредненному потоку) существенно влияет на величину потерь напора; это обстоятельство приходится дополнительно учи­тывать так, как то поясняется в § 4-7.

В некоторых случаях практики при турбулентном движении жидкости в нее можно ввести (в весьма малом количестве) особые полимерные добавки, которые, двигаясь вместе с жидкостью, приглушают турбулентное перемешивание, причем, как показывает опыт, потери напора резко снижаются. Подчеркнем, что, как видно из всего сказанного выше, модель Рейнольдса — Буссинеска (модель осредненного потока), которой для расчета мы заменяем действительный турбулентный поток, представляет собой некоторый особый воображаемый ламинарный поток.

5. Средняя скорость при турбулентном движении жидкости.Не следует смешивать термины «средняя скорость» v и «осредненная скорость» u.[11] В первом случае мы проводили осреднение по живому сечению (для данного момента времени), во втором случае — по времени (в данной точке пространства).

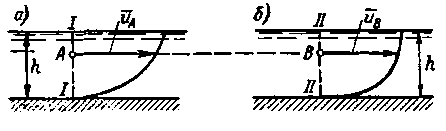
Рис. 4-12. Сопоставление потоков, характеризуемых различной интенсивностью пульсации скоростей

В случае ламинарного движения скорость v есть средняя из действительных скоростей и. В случае же турбулентного движения скорость v есть средняя не из действительных скоростей, а уже из осредненных скоростей; чтобы получить скорость v, в этом случае следует дважды прибегать к осреднению; сперва осредняем продольные скорости по времени в отдельных точках поперечного сечения, а затем полученные и осредняем по поперечному сечению потока.

6^°. Кинетическая энергия турбулентного потока.Изобразим на рис. 4-12 два одинаковых призматических русла; будем считать, что потоки на рис. 4-12 характеризуются одинаковыми расходами Q и одинаковыми глубинами h, а следовательно, одинаковыми средними скоростями v.

Рассмотрим два живых сечения: I - I (рис. 4-12,а) и II - II (рис. 4-12,6). Предположим, что в некоторых двух сходственных точках А и В указанных живых сечений осредненные продольные скорости и_А и и_в оказались равными: u_А = и_в. При таком положении в намеченных сходственных точках (А и В) пульсация скоростей (и_а)_х может быть, вообще говоря, различной; например, в точке А размах пульсации может быть большим (рис. 4-13,а)[12], а в точке В — малым (рис. 4-13,б).

Сопоставляя между собой потоки на рис. 4-12, а и б, легко видеть, что оба эти потока, имея одинаковую среднюю скорость v, в общем случае могут характеризоваться различной структурой. При этом поток с повышенной турбулентностью (рис. 4-13, а) всегда будет обладать большей кинетической энергией.

Можно считать, что кинетическая энергия турбулентного потока слагается из двух величин:

а) кинетической энергии, подсчитанной исходя из осредненных скоростей и;

б) кинетической энергии, подсчитанной исходя из пульсационных скоростей u′.

Если в случае ламинарного режима удельная кинетическая энергия выражается величиной 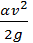, где α — корректив, учитывающий только неравномерность распределения скоростей по живому сечению (корректив кинетической энергии), то в случае турбулентного режима удельная кинетическая энергия выражается величиной 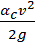, где

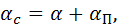(4-54)

причем здесь α_п — дополнительный корректив, учитывающий пульсацию продольных скоростей (и_а)_х в отдельных точках поперечного сечения потока.

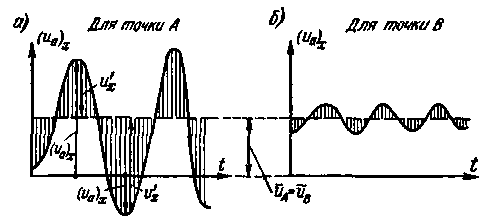
Рис. 4-13. Графики пульсации продольной актуальной скорости для потоков на рис. 4-12

Величину α_п приходится, однако, учитывать только при наличии интенсивной турбулентности, которая может иметь место при неравномерном движении; для турбулентного равномерного движения величиной α_п можно пренебрегать.

Заметим в заключение, что в связи с различной степенью пульсации ско­ростей для потоков на рис. 4-12, а и б, распределение осредненных скоростей и по живым сечениям для этих потоков должно получиться разным (формы эпюры скоростей на рис. 4-12,а и б должны быть различными; см. § 4-7 и 4-8).