В. ПОТЕРЯ НАПОРА ПО ДЛИНЕ ПРИ ТУРБУЛЕНТНОМ УСТАНОВИВШЕМСЯ РАВНОМЕРНОМ ДВИЖЕНИИ ЖИДКОСТИ

Как показывают опыты, величина 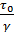(см. § 4-2) может быть выражена через скоростной напор следующим образом:[25]

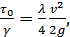(4-67)

где λ/4 — некоторый эмпирический коэффициент пропорциональности.

Сопоставляя (4-67) с (4-15), можем написать:

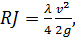(4-68)

откуда, учтя, что J = h_l:l, получаем следующую общую зависимость для потерь напора по длине при равномерном установившемся движении:

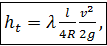(4-69)

где l — длина потока; R — гидравлический радиус.

Для круглых напорных труб D = 4R, и потому для этих труб общая зависимость (4-69) переписывается в виде:

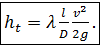(4-70)

Формула (4-70) называется формулой Вейсбаха — Дарcи. Безразмерный коэффициент λ, входящий в нее, будем именовать коэффициентом гидравлического трения.

В случае ламинарного напорного движения жидкости в круглой трубе мы уже получили выше теоретическую формулу (4-46) для λ. При турбулентном течении λ находится по эмпирическим формулам.

Ранее считали, что коэффициент λ, входящий в выражение (4-70), является постоянной величиной; несколько позже его ставили в зависимость от средней скорости v или диаметра D. Некоторые авторы связывали величину λ только с шероховатостью стенок труб. Такого рода зависимости в настоящее время считаются устаревшими и неприемлемыми в практике.

Современные расчетные формулы для λ предусматривают зависимость этого коэффициента в общем случае только от шероховатости стенок русла и от числа Рейнольдса. Величину λ в случае круглых труб можно найти для турбулентного движения (так же как и для ламинарного движения; см. выше), зная закон распределения скоростей по живому сечению.

Действительно, формулу (4-70) можно переписать в виде

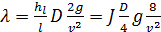(4-71)

и затем, учтя (4-63), в виде

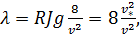(4-72)

откуда

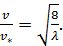(4-73)

Выражение для 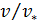можно найти из (4-62). Подставляя такое выражение в (4-73), нетрудно найти зависимость для величины λ.

Л. Прандтль в 1932 г. для гладких труб получил следующую формулу (исходя из некоторой неполной воображаемой модели):

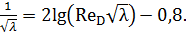(4-74)

Блазиус в 1913 г. на основании обработки многочисленных опытов по исследованию движения жидкости в круглых гладких (латунных) трубах при числах Рейнольдса Re_D от 4000 до 100000 установил эмпирическую зависимость

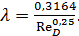(4-75)

Формулы для 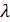в случае шероховатых труб были предложены многими авторами. Прежде чем остановиться на пояснении тех из них, которые в настоящее время главным образом должны рекомендоваться для практического применения, осветим (в следующем параграфе) работу И. Никурадзе, обобщившего при помощи особого графика результаты всех исследований в области вопроса о потерях напора в круглых трубах.

§ 4-10. ИССЛЕДОВАНИЯ И. НИКУРАДЗЕ. ОБОБЩЕНИЕ ВОПРОСА О ПОТЕРЯХ НАПОРА

Представим на рис. 4-23 трубу диаметром D с задвижкой К и двумя пьезометрами П. При помощи задвижки К можно изменять скорость v в трубе, причем для каждой такой скорости, установившейся в трубе, можно по пьезометрам определять (в случае установившегося движения) потерю напора 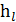на участке трубы длиной l.

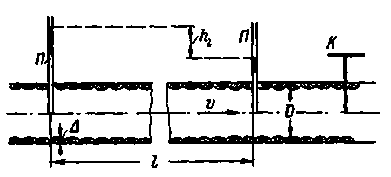
Рис. 4-23. Схема опытов Никурадзе

Коэффициент гидравлического трения λ. согласно формулам (4-70) и (3-135), можно выразить через Re_D:

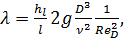
причем по этой формуле, определив а опытов величины 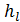, 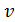и ν, можно вычислять значения λ = f(Re_D).

Проводя подобные опыты, И. Никурадзе исследовал (в 1933 г.) запорные круглоцилиндрические трубы, имеющие однозернистую равномерно распределенную искусственную шероховатость, которую он создавал, наклеивая на стенки трубы песчинки одинаковой высоты Δ на одинаковом расстоянии друг от друга. Результаты своих опытов Никурадзе представил в виде особого графика, по осям которого он отложил безразмерные величины λ и Re_D, причем на таком графике был нанесен ряд кривых, вычисленных в соответствии с приведенной выше зависимостью; каждая кривая отвечала определенной так называемой относительной шероховатости:

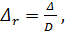(4-76)

где Δ можно назвать «высотой выступов шероховатости» (будем считать, что размер Δ весьма мал сравнительно с диаметром D).

Этот график (см. далее рис. 4-24) позволил в удобной форме обобщить вопрос о потерях напора (в случае равномерного установившегося движения несжимаемой жидкости в круглой трубе) и наглядно показать следующее:

1) коэффициент λ, входящий в формулы (4-69) и (4-70), в самом общем случае зависит только от 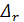и Re_D;

2) имеются частные случаи движения жидкости, когда λ зависит или только от 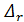, или только от Re_D;

3) имеются вполне определенные зоны сочетания λ и Re_D, для которых в формулах, выражающих пропорциональность (::) 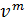величине ,

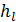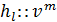(4-77)

показатель степени m приобретает вполне определенное значение (равное единице, двум и т.п.).

На рис. 4-24 показана схема графика Никурадзе. Пользуясь ею, поясним основные положения, вытекающие из рассмотрения данного графика, на котором показаны две «опорные» прямые: прямая I, построенная по уравнению (4-46) (см. линию 1 - 2 - 3); эта прямая называется прямой ламинарного режима; прямая II, построенная исходя из уравнения Блазиуса (4-75); назовем ее прямой Блазиуса.

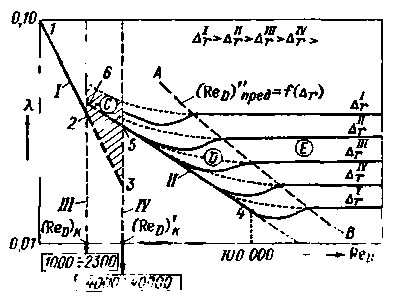
Рис. 4-24. Схема графика Никурадзе (кривые λ =f(Re_D) для различных 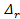,) I - зона ламинарного режима, С - зона неустойчивого (переходного) режима, II - область гладких русел турбулентной зоны, D - область доквадратичного сопротивления шероховатых русел турбулентной зоны, Е - область квадратичного сопротивления шероховатых русел турбулентной зоны

Откладывая в соответствующем масштабе по осям графика величины lgRe_D (по горизонтальной) и lgλ, (по вертикальной), мы на шкалах осей выписываем сами числа Re_D и λ (а не величины их логарифмов). Построение графика в таких логарифмических координатах позволяет «опорные» линии I и II, выражаемые степенными функциями, представить в виде прямых.

Все поле графика можно разбить на три зоны:

Первая зона - зона ламинарного режима; она представлена отрезком прямой 1-2, построенной по уравнению (4-46). Здесь экспериментальные кривые
λ = f(Re_D), найденные для разных 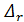, сливаются в одну прямую линию, совпадающую с линией 1-2.

Для этой зоны имеем следующее:

а) величины Re_D относительно малы, менее (Re_D)_K = 1000 ÷ 2300 [см. формулу (3-136)];

б) потеря напора 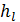не зависит от шероховатости, так как все кривые

λ = f(Re_D), построенные для разных 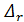, как то было отмечено, сливаются

в одну прямую 1 - 2;

в) потери напора прямо пропорциональны первой степени скорости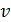

[как то следует из формул (4-45) и (4-46); в данном случае показатель

степени m = 1];

г) величина λ определяется формулой (4-46).

Вторая зона - зона, расположенная между вертикалями III и IV (заштрихована), является зоной неустойчивого режима (см. § 3-24; зону (3) на рис. 3-42). Ее называют, как было отмечено выше, неустойчивой или переходной зоной (зоной, внутри которой происходит переход ламинарного режима в турбулентный и наоборот - турбулентного режима в ламинарный). Здесь:

а) числа Рейнольдса лежат в пределах от 1000 ÷ 2300 до 4000 ÷ 40000;

б) при движении жидкости по трубе на отдельных участках возникают

отдельные области турбулентного режима, которые разрастаются, а затем

исчезают и снова появляются. В связи с этим данная зона иногда называется

зоной перемежающейся турбулентности.

Заметим, что когда турбулентные области в трубе разрастаются, растет и сопротивление движению жидкости (в связи с ростом турбулентных касательных напряжений трения), при этом скорость 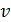уменьшается. Как только она делается меньше критической скорости, разросшиеся турбулентные области обращаются в ламинарные (или выносятся за пределы рассматриваемой части потока); после этого в связи с уменьшением потерь напора (обусловленным переходом турбулентного режима в ламинарный на отдельных участках трубы) скорость 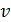увеличивается, причем турбулентные области снова появляются и т. д. В связи с таким характером движения в переходной зоне, представить это движение на графике какими-либо определенными кривыми нет возможности. Исключение здесь могут составить только случаи, когда ламинарный режим «затягивается» и имеет место по длине всего трубопровода (см. прямую 2 - 3) или, когда в связи с особыми условиями движения турбулентный режим имеет место по длине всего трубопровода (см. линию 5 - 6).

Дополнительно надо иметь в виду еще следующее обстоятельство, которое может затруднять определение потерь напора (и, следовательно, величин λ) для области неустойчивого режима.

Можно допустить, что при Q = const (а следовательно, и при 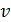= const) кинетическая энергия жидкости, находящейся в трубе (между рассматриваемыми пьезометрами; рис. 4-23) при турбулентном и ламинарном режимах является различной по величине. Такое положение обусловливается тем, что коэффициент α при ламинарном и турбулентном режимах имеет различное значение, кроме того, при турбулентном режиме происходит пульсация скоростей. В указанном случае при смене режимов разность показаний пьезометров не будет равна искомой потере напора 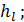она будет равна величине 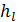плюс соответствующий так называемый инерционный напор (поясняемый далее в гл. 9), который определить в данном случае нет возможности.

Третья зона - зона турбулентного режима; эта зона располагается правее вертикали IV, отвечающей Re_D ≈ 4000 ÷ 40000. Данная зона в свою очередь разбивается на три области.

Первая область - «область гладких русел»; она представлена: а) при числах Рейнольдса Re_D < 100000 - прямой линией II и б) при числах Рейнольдса Re_D > 100000 - кривой линией, являющейся продолжением прямой II; данная кривая, начинающаяся от точки 4, на. рис. 4-24 не показана (она будет представлена далее на рис. 4-25 в виде самой нижней кривой линии). Для первой области имеем:

a) 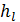в пределах до чисел Re_D= 100000 прямо пропорционально скорости 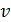в степени 1,75 (m = 1,75), как то следует из формул (4-70) и (4-75);

б) h, не зависит от шероховатости, поскольку все кривые Δ_r= const сливаются в одну линию (здесь мы получаем гладкие трубы; выступы шероховатости покрыты ламинарным подслоем);

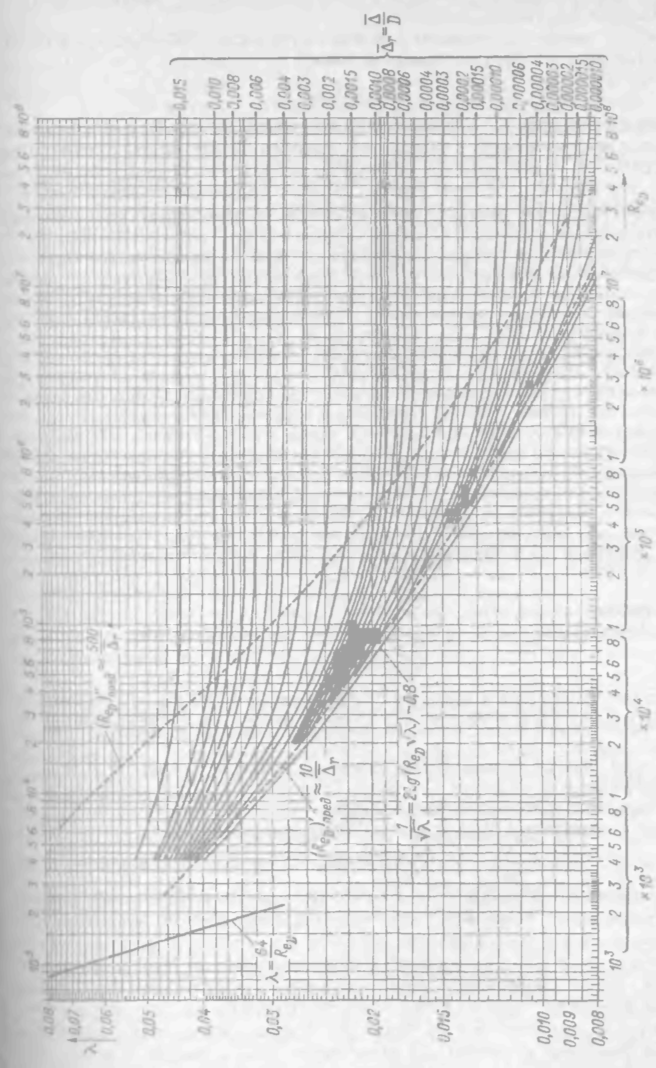
в) h_t а также X, зависит только от числа Рейнольдса, согласно формуле Блазиуса (4-75) или Прандтля (4-74),

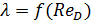(4-78)

Вторая область — «область доквадратичного сопротивления шероховатых русел», эта область лежит между прямой II и линией АВ.

Согласно Никурадзе, кривые Δ_r = const в этой области имеют вид, показанный сплошными линиями; согласно опытам ряда других авторов, эти кривые имеют другой вид (см. штриховые линии). Такое расхождение объясняют различием геометрических форм шероховатости, имевшей место при проведении опытов. Считают, что кривые Никурадзе относятся к однозернистой равномерно распределенной шероховатости; штриховые же кривые — к шероховатости разнозернистой, свойственной, например, стальным и чугунным трубам.

Из сказанного выше ясно, что на левой границе рассматриваемой области кривые графика, опускаясь вниз, характеризуются в месте отрыва их от опорной прямой II показателем степени т, входящим в формулу (4-77), равным 1,75 На правой границе АВ области, где кривые графика переходят в горизонтальные прямые, m = 2,0 (см. ниже). Можно показать, что поднимающиеся кверху сплошные линии Никурадзе (расположенные внутри рассматриваемой области), характеризуются показателем степени т > 2,0. Отсюда заключаем, что т в пределах данной области изменяется от 1,75 до 2,0, причем для однозернистой равномерно распределенной шероховатости этот показатель, согласно Никурадзе, в промежутке между т = 1,75 и т = 2,0 должен иметь максимум (т_макс > 2,0); для разнозернистой же шероховатости, по данным других авторов, показатель т в пределах данной области монотонно возрастает от 1,75 до 2,0.

Из графика видно, что для данной области λ, а также h_l зависят как от числа Рейнольдса, так и от относительной шероховатости:

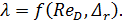(4-79)

Третья область — «область квадратичного сопротивления шероховатых русел»; эта область располагается правее линии АВ. Здесь:

а) потеря напора прямо пропорциональна квадрату скорости v (т = 2,0);

б) коэффициент X не зависит от числа Рейнольдса Re_D (все линии
графика — прямые, параллельные горизонтальной оси);

в) h_l и λ зависят от относительной шероховатости:

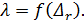(4-80)

В заключение необходимо отметить, что общий качественный характер связей, полученный Никурадзе для круглоцилиндрических напорных труб, разумеется, можно распространить и на потоки другого вида (напорные и безнапорные). Важно подчеркнуть, что после работы Никурадзе стало совершенно ясно, что при выполнении любых гидравлических расчетов нет надобности различать жидкости разного вида (как то делали ранее, когда предлагали отдельные расчетные формулы для вычисления потерь напора в случае воды, нефти, разных масел и т. п.). Именно из рассмотрения графика Никурадзе делается очевидным, что в гидравлике при определении потерь напора следует иметь в виду жидкость вообще, движение которой характеризуется безразмерным числом Рейнольдса определенной величины (зависящим, в частности, от таких физических характеристик рассматриваемой жидкости, как ее коэффициент вязкости и ее плотность).