ПРАКТИЧЕСКИЕ СПОСОБЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГО ТРЕНИЯ X ДЛЯ НАПОРНЫХ ТРУБ (КРУГЛЫХ И НЕКОТОРЫХ ПРЯМОУГОЛЬНЫХ). ПРИМЕРЫ РАСЧЕТА

Как было отмечено выше, различают шероховатые трубы, имеющие однозернистую шероховатость (с которыми работал Никурадзе) и трубы, имеющие разнозернистую шероховатость (когда выступы шероховатости имеют неодинаковую форму и размеры, расстояние между ними также различно). Трубы, обычно встречающиеся в практике, так называемые технические, имеют разнозернистую шероховатость или являются гладкими. Ниже поясним расчет технических труб.

1°. Напорные шероховатые технические трубы (трубы с разнозернистой шероховатостью). Для этих труб в 1938 г. Кольбрук на основании своих опытов, а также с учетом исследований других авторов, предложил формулу:

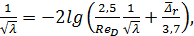(4-81′)

где 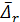— осредненная относительная шероховатость [см. формулу (4-76)]. По этой формуле был построен график[26] (рис. 4-25). Пользуясь этим графи-ком, можно определить коэффициент λ в случае технических труб для всех трех областей турбулентной зоны.

Для квадратичной области сопротивления шероховатых труб формула (4-81′) упрощается и приобретает вид формулы Прандтля (предложенной им для шероховатых труб):

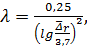(4-81′′)

Для технических труб под величиной 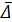понимают некоторую среднюю высоту выступов шероховатости. Такую осредненную геометрическую характеристику 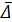установить для рассматриваемой трубы путем непосредственного измерения выступов шероховатости нельзя. Поэтому при определении среднего значения 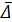для данной трубы поступают следующим образом.

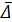Рассматривают квадратичную область сопротивления и для этой области опытным путем, пользуясь формулой (4-70), находят для данной трубы величину λ. Затем по формуле (4-81") вычисляют искомое значение. Найденное таким образом среднее значение называют эквивалентной шероховатостью.

Эквивалентная шероховатость зависит: а) от материала и способа изго-товления и соединения труб, б) от продолжительности эксплуатации труб, в процессе которой могут возникнуть коррозия стенок или инкрустации (образование наростов на стенках). Численные значения эквивалентной шероховатости 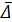, найденные указанным путем для разных труб, приводятся в табл. 4-2. По этой таблице и определяют 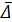при выполнении практических расчетов.

Таблица 4-2

Шероховатость труб и каналов[27]

Характеристика поверхности труб и каналов	, мм
I. Цельнотянутые трубы
Из латуни ................................................................................	0,0015-0,0100
Новые стальные .....................................................................	0,020-0,100
Стальные водопроводные, находящиеся в эксплуатации..	1,20-1,50
II. Цельносварные стальные трубы
Новые или старые в хорошем состоянии ............................	0,04-0,10
Бывшие в эксплуатации ........................................................	≈ 0,10-0,15
С двойной поперечной клепкой, сильно корродированные	2,0
III. Чугунные трубы
Новые.......................................................................................	0,25-1,00
Новые битумизированные.....................................................	0,10-0,15
Асфальтированные.................................................................	0,12-0,30
Бывшие в эксплуатации, корродированные........................	1,0-1,5
IV. Бетонные и асбестоцементные трубы
Бетонные трубы при хорошей поверхности с затиркой.....	0,3-0,8
Бетонные трубы при среднем качестве работ......................	2,5
Бетонные трубы с грубой (шероховатой)поверхностью....	3,0-9,0
Асбестоцементные трубы новые..........................................	0,05-0,10
Асбестоцементные трубы, бывшие в эксплуатации...........	≈0,60
V. Деревянные и стеклянные трубы
Деревянные трубы из тщательно остроганных досок........	0,15 ориентировочно 0,30   0,70
Деревянные трубы из хорошо отстроганных досок............
Деревянные трубы из нестроганных хорошо пригнанных досок.........................................................................................
Трубы из чистого стекла........................................................	0,0015-0,0100
VI. Облицовка каналов
Хорошая штукатурка из чистого цемента............................	0,05-0,22
Штукатурка цементным раствором с ожелезнением..........	0,5
Штукатурка по металлической сетке....................................	10-15
Шлакобетонные плиты..........................................................	1,5

Зная для данной трубы 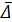, находим по (4-76) значение 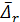; затем по формуле (3-135) определяем Re_D. Имея для рассматриваемой трубы 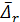, и Re_D, можем найти λ по графику на рис. 4-25 или по формулам (4-81).

Формула (4-81')неудобна для вычисления (величину λ по этой формуле приходится находить подбором). А. Д. Альтшуль предложил вместо зависимости (4-81') более простую формулу:

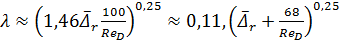, (4-82′)

которая для квадратичной области сопротивления приводится к формуле Шифринсона:

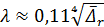, (4-82′′)

этой последней формулой можно пользоваться вместо формулы (4-81′) только при 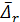< 0,007.

В случае прямоугольных труб с соотношением сторон поперечного сечения, лежащем в пределах от 0,5 до 2,0, величина λ может определяться также по приведенному графику или по формулам (4-81) и (4-82); здесь только под D надо понимать так называемый гидравлический диаметр

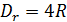, (4-83)

где R — гидравлический радиус рассматриваемой прямоугольной трубы (заметим, что для круглой трубы гидравлический диаметр оказывается равным геометрическому диаметру: D_r = D).

Обратим внимание, что на рис. 4-25 нанесены две пунктирные кривые, выделяющие область доквадратичного сопротивления, характеризующуюся зависимостью (4-79). Числа Рейнольдса, отвечающие этой области, лежат в пределах

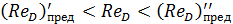(4-84)

В случае

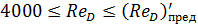(4-85)

получаем область, которую практически следует рассматривать как область гладких труб (см. ниже п. 2^°), для которых практически действует зависимость (4-78). В случае же

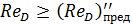(4-86)

имеем квадратичную область сопротивления, для которой справедлива зависимость (4-80).

Согласно А. Д. Альтшулю, предельные числа Рейнольдса 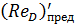и 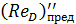с некоторым приближением могут быть найдены по формулам:

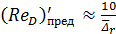; (4-87)

(4-88)

Пользуясь приведенными зависимостями, можно решить вопрос о том:

а) когда данная труба должна рассматриваться как практически гладкая и ее можно рассчитывать, не считаясь с выступами шероховатости;

б) когда данную трубу следует рассчитывать по зависимостям, относящимся к области квадратичного сопротивления, не считаясь с величиной чисел Рейнольдса.

Не следует смешивать критические числа Рейнольдса (нижнее и верхнее) с предельными числами Рейнольдса, выделяющими область доквадратичного сопротивления.

2°. Напорные гладкие технические трубы. В этом случае формулы
(4-81′) и (4-82") упрощаются и приобретают вид уже известных нам формул Прандтля (4-74) и Блазиуса (4-75). Как уже отмечалось, формула (4-75) дает достаточно точные результаты в случае

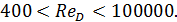(4-89)

При любых Re_D > 4000 можно пользоваться формулой (4-74) или более простой зависимостью, предлагаемой рядом авторов:

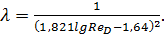(4-90)

Расчет прямоугольных гладких труб выполняется так, как указано в п. 1°.

3°. Дополнительные замечания. Вслучае стальных и чугунных водопро­водных труб, уже находившихся в эксплуатации, величину X в последнее время рекомендуют иногда определять по эмпирическим формулам Ф. А. Шевелева:

а) при Re_D ≥ 9,2 • 10⁵ (квадратичная область сопротивления)

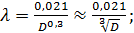(4-91)

б) при Re_D ≤ 9,2 • 10⁵ (доквадратичная область сопротивления)

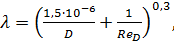(4-92)

где D всюду выражается в метрах.

В случае расчета стальных труб со сварными стыками, при которых образуются наплывы металла, иногда дополнительно учитывают по различным эмпирическим формулам (здесь не приводим) влияние этих стыков на величину λ.

В заключение обратим внимание на следующее.

Как видно из графиков рис. 4-24 и 4-25, для квадратичной области сопро­тивления величина λ не зависит от Re_D. Имея это в виду и рассматривая напорное движение в некоторой трубе, длиной l₀ = const и диаметром D = const при расходе Q = const, а следовательно, и при скорости v = const, можем заключить, что для этой трубы, согласно упомянутым графикам, с уменьшением вязкости (т. е. с уменьшением v) число Реинольдса Re_D будет расти; вместе с тем потери напора (несмотря на уменьшение вязкости) будут оставаться, согласно формуле (4-70), постоянными.

Такой парадокс, по-видимому, можно объяснить следующим образом. С уменьшением v характер турбулентности будет изменяться: она, надо полагать, будет развиваться все более и более; при этом длины путей пробега l отдельными частицами жидкости (от начального сечения 1 - 1 до конечного сечения потока 2 - 2, т. е. от начала трубы до ее конца) должны увеличиваться: длина пробега (длины траекторий) l будет все больше и больше отличаться от длины трубы l₀ (l > l₀); равным образом должны как-то изменяться и величины относительных перемещений (Δl )отдельных струек по отношению друг к другу. По-видимому, следует считать, что для квадратичной области сопротивления мы должны получать как бы такое равенство ( 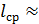const, где 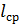— средняя длина пробега частицами жидкости от начала трубы до ее конца; 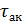— среднее актуальное касательное напряжение вдоль 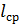(зависящее, разумеется, от величин Δl).

Как видно, получается следующая картина: с уменьшением v уменьшается 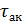; но зато, в связи с изменением характера турбулентности увеличивается ( 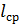), причем отмеченное выше произведение ( 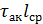), от которого должны зависеть потери напора, сохраняет свою величину.

Дополнительно надо иметь в виду, что в момент, когда v обращается в нуль, мы получаем идеальную (а следовательно, воображаемую) жидкость, при возникновении которой скорость на стенке русла «скачком» должна измениться от нуля (в случае реальной жидкости) до соответствующей конечной величины (u= const по живому сечению) — в случае идеальной жидкости. При этом здесь получится (при λ = 0) или воображаемый турбулентный поток идеальной жидкости, или воображаемый ламинарный поток идеальной жидкости.

Разумеется, описанный «парадокс» может быть также осознан, исходя из рассмотрения не действительной картины движения жидкости (которую мы имели в виду выше), а из рассмотрения «модели осредненного потока».[28]

Примеры расчета.[29]

№ 1. Дана цельносварная цилиндрическая стальная труба круглого поперечного сечения, бывшая в употреблении, но в хорошем состоянии. Диаметр трубы D = 120 мм: длина ее l = 500 м. По трубе движется керосин, имеющий температуру t = 15⁰С; расход керосина Q = 6 л/с = 0,006 м³/с.

Требуется:

а) установить режим движения керосина в трубе;

б) если режим движения керосина турбулентный, то определить область сопротивления, отвечающую заданным условиям движения;

в) найти величину потерь напора 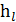, по длине для заданного трубопровода.

Решение. Шероховатость стенок трубы, согласно табл. 4-2, Δ = 0,04мм.

Относительная шероховатость трубы

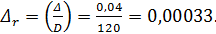
Кинематический коэффициент вязкости для керосина при температуре 15⁰С, согласно табл. 4-1, v = 0,027 см²/с.

Средняя скорость движения керосина в трубе

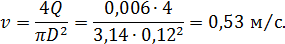
Число Рейнольдса

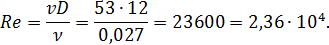
Предельные числа Рейнольдса, согласно формулам (4-87) и (4-88),

;

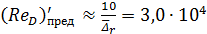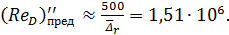
Сопоставляя величину Re_D с предельными числами Рейнольдса, видим, что 4000 < Re_D < 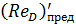, где 4000 — число Рейнольдса, отвечающее началу турбулентной зоны.

Таким образом, в нашем случае должен иметь место турбулентный режим, относящийся к области гладких русел.

Согласно графику на рис. 4-25, для найденных Δ_r и Re_D величина λ = 0,025.

По формуле Блазиуса (4-75):

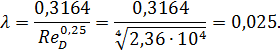
Потеря напора

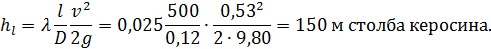
№ 2. Для тех же условий, что и в предыдущем примере (для движения в трубе керосина), определить коэффициент λ и потерю напора на заданном участке трубопровода, если Q = 40 л/с.

Решение. Средняя скорость

.

Число Рейнольдса

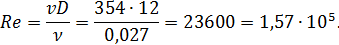
Сопоставляя это число с предельными чисчами Рейнольдса, найденными в предыдущем примере, видим, что

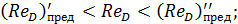
отсюда заключаем, что в данном случае будем иметь область доквадратичного сопротивления турбулентной зоны.

Для найденного Re_D и установленной в предыдущем примере Δ_г, согласно графику рис. 4-25,

λ = 0,0186

Значение λ по формуле (4-81′) получается

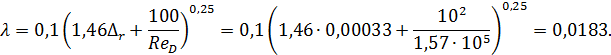
Потеря напора h_l по длине заданного трубопровода

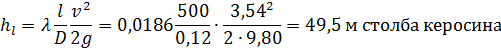
№ 3. Дана круглая цельносварная стальная труба, бывшая в эксплуатации, характеризуемая величиной Δ = 0,15 мм. Диаметр трубы D = 0,5 м: длина ее l = 500 м. По трубе движется вода, имеющая температуру 50 С. Расход воды Q = 0,60 м³/с

Требуется найти потерю напора по длине трубы.

Решение. Относительная шероховатость трубы

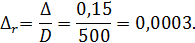
Кинематический коэффициент вязкости для воды заданной температуры, согласно табл. 4-1, v = 0,00556 см²/с.

Средняя скорость движения воды в трубе

.

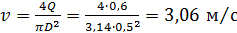Число Рейнольдса

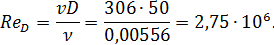
Предельные числа Рейнольдса, согласно формулам (4-87) и (4-88),

;

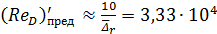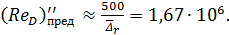
Сопоставляя величину Re_D с предельными значениями чисел Рейнольдса, видим, что

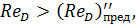
т. е. в данном случае имеет место область квадратичного сопротивления турбулентной зоны. Для найденных Δ_r и Re_D, согласно графику рис. 4-25, λ, = 0.015.

Значение λ по формуле (4-82') оказывается

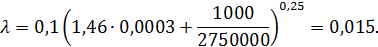
Искомая потеря напора

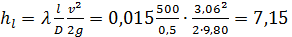м столба воды, имеющей температуру 50° С.