ТУРБУЛЕНТНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ В ОСРЕДНЕННОМ ПОТОКЕ

В действительном турбулентном потоке имеются обычные касательные напряжения τ, называемые актуальными. Поле таких напряжений, в связи с турбулентностью, должно изменяться во времени. Если бы для данного момента времени нам было известно такое поле, то мы могли бы для этого момента времени, используя обобщенный закон Ньютона (см. сноску на с. 136), вычислить с некоторым приближением и поле актуальных касательных напряжений.

«Турбулентные касательные напряжения» τ_т не следует смешивать с актуальными напряжениями т действительного турбулентного потока. Напряжения τ_т не существуют в действительном потоке; они являются воображаемыми; их мысленно вводят в осредненный поток (в модель Рейнольдса — Буссинеска), чтобы в определенном отношении (см. ниже) приблизить модель осредненного потока к действительности.

Поясним этот вопрос подробнее.

Переходя от действительного турбулентного потока к осредненному потоку (к модели), мы отбрасываем поперечные пульсационные скорости u'_z = u_z. В модели осредненного потока остаются только продольные составляющие скоростей, т. е. величины их (которые условно обозначают буквой u)

Вместе с тем, отброшенные скорости u_z влияют на формирование эпюры продольных скоростей и, а следовательно, влияют и на величину потерь напора.

Имея это в виду, чтобы компенсировать влияние (на эпюру продольных скоростей) отбрасываемых скоростей u_z, и было предложено ввести в модель осредненного потока воображаемые (несуществующие) продольные касательные напряжения τ_т. При этом величину τ_т. стремятся подобрать так, чтобы количественное влияние τ_т. на эпюру скоростей и соответствовало количественному влиянию на эту же эпюру отброшенных поперечных скоростей u_z,.

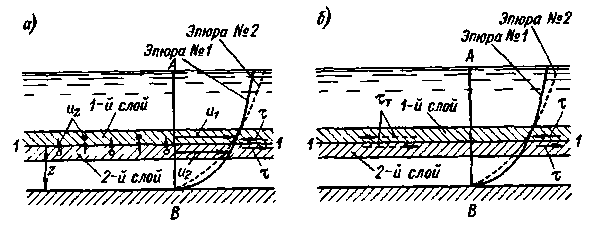
Рис. 4-14. К вопросу о турбулентных касательных напряжениях: а — «действительный» поток; имеет место поперечный обмен частицами жидкости (исключенный при переходе к осредненному потоку); б — модель осредненного потока; введены воображаемые касательные напряжения τ_т (компенсирующие исключенные скорости и_z)

На рис. 4-14, а представлена схема действительного потока, который характеризуется наличием поперечного обмена частицами жидкости: см. на рисунке «черные» частицы, которые имеют относительно большие продольные скорости и₁ причем эти частицы со скоростью u_z↓ переходят в нижний (2-й) слой жидкости и ускоряют его движение; см. также на этом рисунке «белые» частицы, которые имеют относительно малые продольные скорости u_z, причем они со скоростью и_z↑ переходят из 2-го слоя в 1-й слой жидкости и замедляют движение этого слоя. На схеме а показаны две эпюры скоростей: эпюра № 1 —действительная эпюра продольных скоростей и и эпюра № 2 — искаженная эпюра, получающаяся в том случае, если исключим из рассмотрения скорости u_z[13].

На рис. 4-14,6 показана схема модели Рейнольдса — Буссинеска, которая характеризуется отсутствием турбулентного обмена (u_z = 0); для такой схемы мы должны получить упомянутую выше искаженную эпюру скоростей № 2; однако, вводя в эту схему вместо скоростей u_z воображаемые касательные напряжения τ_т (соответствующей величины), мы можем исправить искаженную эпюру № 2 и получить вместо нее «истинную» эпюру № 1.[14]Как видно, в действительном потоке (схема а) действуют только «ньютоновские касательные напряжения» τ. (§ 4-3); в модели Рейнольдса — Буссинеска (схема б) вдоль поверхности 1 — 1 действуют касательные напряжения равные (τ + τ_т).

Чтобы определить необходимую величину τ_т, используют как бы постулат, который условно можно представить такой записью:[15]

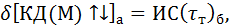
где в левой части уравнения приводится приращение количества движения (КД) некоторого элементарного объема жидкости на соответствующем его перемещении, обусловленное турбулентным обменом; как видно, эта часть уравнения относится к действительному потоку (рис. 4-14,а); в правой части уравнения приводится импульс воображаемых сил трения (на соответствующем перемещении); эта часть уравнения относится к воображаемому потоку (рис. 4-14,6).

Из сказанного, между прочим, вытекает, что приведенная выше зависимость не может быть названа уравнением количества движения (импульса сил), поскольку левая и правая части этого уравнения относятся к различным объектам: левая к действительному потоку, а правая — к воображаемому потоку.

Решая особым (весьма приближенным) способом уравнение, отражаемое приведенной выше условной записью, Буссинеск получил формулу для τ_т, по своей структуре совпадающую с зависимостью (4-24):[16]

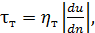(4-55)

где 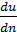- градиент скорости; он имеет тот же смысл, что и в зависимости (4-24); здесь только под u надо понимать осредненную продольную скорость;[17] 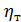- коэффициент пропорциональности, называемый динамическим коэффициентом турбулентной вязкости или турбулентного обмена.[18]

Согласно Л. Прандтлю коэффициент 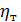выражается зависимостью (полученной в предположении отсутствия молекулярной вязкости):

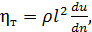(4-56)

где величину l принято называть длиной пути смешения или перемешивания; разные авторы приписывают величине l различный физический смысл; данную величину выражают в виде

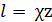(4-57)

где z — расстояние от стенки русла до точки, в которой определяется турбу-лентное касательное напряжение; χ — «универсальная постоянная Прандтля»; согласно опытам Никурадзе для круглой трубы χ«0,4.

Как видно из (4-56), величина динамического коэффициента 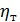пропор-циональна градиенту скорости, причем коэффициент 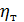в отличие от коэф-фициента 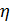(коэффициента молекулярной вязкости) зависит от характера движения жидкости.

Аналогично (3-128) можем написать [учитывая также зависимость (4-56)]:

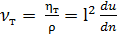, (4-58)

где 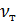называется кинематическим коэффициентом турбулентной вязкости или турбулентного обмена.

В общем случае осредненный поток должен одновременно обладать и молекулярной и турбулентной вязкостями. Поэтому полное суммарное касательное напряжение τ. записывают иногда (с некоторым приближением) в виде

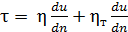, (4-59)

В случае ламинарного движения второй член правой части (4-59) отпадает; при этом напряжение трения на стенке 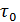получается пропорциональным первой степени средней скорости. В случае турбулентного движения при достаточно больших числах Рейнольдса второй член правой части (4-59) значительно превышает первый; при этом с молекулярной вязкостью можно вовсе не считаться; в результате τ оказывается прямо пропорциональным второй степени средней скорости (см. ниже § 4-9).

В случае турбулентного движения в условиях не слишком больших чисел Рейнольдса оба слагаемых правой части (4-59) могут получиться соизмеримыми, причем 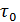оказывается пропорциональным средней скорости в степени, не равной двум.

Для осредненного турбулентного потока, когда действует зависимость (4-59), эпюра турбулентных касательных напряжений 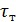для круглой трубы может быть схематично представлена площадью Оса (см. рис. 4-4); на этом рисунке через 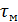обозначены касательные напряжения, обусловленные молекулярной вязкостью.

Необходимо учитывать, что при желании описать то или другое достаточно сложное физическое явление (например, явление турбулентного движения жидкости) приближенной математической зависимостью, устанавливающей связь между различными характеристиками (параметрами) данного явления, часто поступают следующим образом. Сперва создают в своем воображении так называемую неполную модель данного явления (неполную в том смысле, что эта модель не полностью отражает рассматриваемое явление, несколько схематизируя, упрощая его). После этого подвергают анализу с использованием аппарата механики и математики не действительность (которая сложна и поэтому недоступна указанному анализу), а принятую неполную воображаемую модель. Именно, исходя из такой модели, и получают соответствующие расчетные зависимости и формулы. Само собой разумеется, что эти зависимости могут считаться приемлемыми только после экспериментальной их проверки (и часто после введения в них соответствующих поправочных коэффициентов, учитывающих отличие принятой модели от действительности). Различные авторы при исследовании определенного явления могут принимать различные модели и получать при этом разные результаты. Само собой разумеется, что удачной моделью будет та, которая приведет нас к результатам, достаточно хорошо согласующимся с опытными данными. Иногда мы можем столкнуться с таким случаем, когда модель, по своему виду больше отличающаяся от действительности, дает лучшие количественные результаты, чем модель, отличающаяся от действительности в меньшей мере и т. п.

Именно с учетом высказанных соображений и следует рассматривать решения, упоминавшиеся выше, а также решения, о которых мы будем говорить в последующем изложении.

Из вывода, приведенного в § 2-2, можно видеть, что, прилагая к граням рассматриваемой в этом параграфе призмы касательные напряжения, мы при этом должны изменить величину нормальных напряжений с тем, чтобы элементарная призма осталась в равновесии (в данном случае в «динамическом равновесии»). Поэтому можно утверждать, что осредненный поток (модель Рейнольдса — Буссинеска) должен характеризоваться наличием не только дополнительных турбулентных касательных напряжений, но и наличием еще дополнительных турбулентных нормальных напряжений.

В заключение отметим, что рассматривая осредненный поток вязкой (реальной) жидкости и прилагая к нему уравнение Навье — Стокса (см. § 3-3), Рейнольдс получил три особых уравнения равновесия жидкости, учитывающих осреднение потока во времени. Эти уравнения, «содержащие некоторые дополнительные члены, называются уравнениями Рейнольдса (их мы не приводим).