УСТАНОВИВШЕМСЯ ДВИЖЕНИИ ЖИДКОСТИ

Рассмотрим напорное движение в круглоцилиндрической трубе (рис. 4-6). Найдем сперва величину расхода Q для этой трубы. Напишем выражение для элементарного расхода dQ, проходящего через элементарную часть площади живого сечения dω в виде «кольца» радиусом r (см. чертеж):

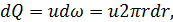(4-37)

где

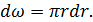
Подставляя в (4-37) выражение (4-35), имеем

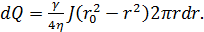(4-38)

Интегрируя это выражение по всей площади живого сечения, получаем объем отмеченного в § 4-4 параболоида вращения, равный

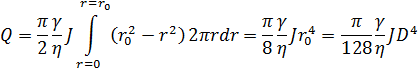
или

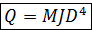(4-39)

где коэффициент М зависит только от рода жидкости:

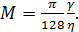(4-40)

Средняя скорость

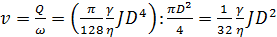(4-41)

или

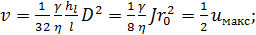(4-42)

как видно

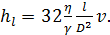(4-43)

Формула (4-39) была впервые получена доктором медицины Пуазейлем в 1840 г., причем он пришел к этой зависимости чисто эмпирическим путем, исследуя движение жидкости в тонких капиллярных трубках. Из рассмотрения зависимости (4-43) можно сделать следующие существенные выводы.

В случае ламинарного движения потеря напора h_l:

1) зависит от свойств жидкости, что учитывается коэффициентом вязкости η, а также величиной γ:

2) прямо пропорциональна средней скорости ν в первой степени;

3) не зависит от шероховатости стенок русла — в формулу (4-43) не входят какие-либо характеристики шероховатости стенок русла.

Потерю напора h_l, для круглоцилиндрической трубы в случае ламинарного режима иногда представляют в виде

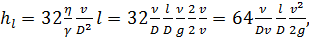(4-44)

откуда

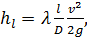(4-45)

где (при ламинарном режиме):

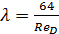(4-46)

причем, как видно, коэффициент λ, называемый «коэффициентом гидравлического трения», зависит здесь от скорости v (входящей в выражение для ).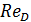

Можно показать, что в данном случае (ламинарного равномерного движения) при найденной выше параболической форме эпюры скоростей потери напора получаются минимально возможные.