ВЕЛИЧИНА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ В СЛУЧАЕ ЖИДКОСТИ, НАХОДЯЩЕЙСЯ ПОД ДЕЙСТВИЕМ ТОЛЬКО ОДНОЙ ОБЪЕМНОЙ СИЛЫ - СИЛЫ ТЯЖЕСТИ

Будем рассматривать как в этом параграфе, так и в последующих (за исключением § 2-9), жидкость, на которую действует только одна объемная сила - сила тяжести.

Представим на рис. 2-8 закрытый сосуд, в котором находится жидкость. Обозначим через p₀ внешнее поверхностное давление (т. е. давление на свободную поверхность жидкости). Возьмем оси координат, как показано на чертеже, и наметим точку m, у которой выделим единицу массы тяжелой жидкости. К этой единице массы приложена объемная сила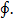

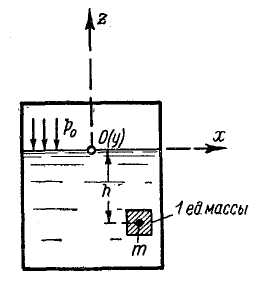
Рис. 2-8. Давление р для «тяжелой жидкости»

В случае, когда объемными силами, действующими на жидкость, являются только силы тяжести, имеем

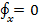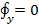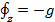, , (2-28)

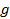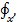
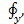
где - ускорение силы тяжести; 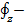проекции силы 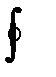на оси координат.

Величина dp выражается зависимостью (2-18), где dU в нашем случае будет равно [см. (2-19)]:

dU = 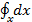+ + 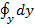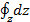= - 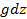. (2-29)

Подставляя (2-29) в (2-18) [или (2-28) в (2-14)], можем написать:

dp = -ρ 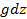. (2-30)

Интегрируя (2-30), имеем

p = -ρ 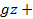C (2-31)

или [см. формулу (1-5)]

p = -γz +C, (2-31’)

где С - постоянная интегрирования. Для определения С рассмотрим точку на поверхности жидкости (где z=0 и p=p₀), тогда согласно (2-31’) для этой точки

C = p₀; (2-32)

в результате вместо (2-31’) имеем:

p =p₀ - γz. (2-33)

Обозначим через h заглубление точки m под свободной поверхностью жидкости:

h= -z, (2-34)

тогда (2-33) окончательно можно переписать в виде:

p =p₀ + γz. (2-35)

где р является абсолютным давлением в рассматриваемой точке; р₀ - внешнее поверхностное давление.

Величина

γh = p_в (обозначение), (2-36)

в формуле (2-35) может быть названа весовым давлением: как видно, p_в представляет собой ту часть абсолютного давления р, которая обусловлена весом самой жидкости.

Из рассмотрения (2-35) заключаем, что абсолютное давление в точке равно сумме внешнего поверхностного давления и весового давления.

Из (2-35) также ясно, что на сколько увеличивается внешнее поверхностное давление р₀, на столько же должно увеличиться и абсолютное давление в данной точке.

Если сосуд открыт, то

p₀ = p_a,

где p_a - атмосферное давление; при этом вместо (2-35) имеем:

p = p_a + γh. (2-37)

Назовем избыточным (сверхатмосферным) давлением величину превышения абсолютного давления в точке над атмосферным давлением, т. е. разность (p - p_a). Эту разность также иногда называют манометрическим давлением.

В практике главным образом приходится сталкиваться не с абсолютным давлением, а с избыточным давлением. Имея это в виду, в дальнейшем будем применять следующие обозначения: 1) для избыточного давления р; 2) для абсолютного давления p_A.

В соответствии с такого рода изменением обозначений имеем:

p = p_A - p_a, (2-38)

причем расчетная формула (2-35) принимает вид:

а) для закрытого сосуда

(2-39)

б) для открытого сосуда

(2-40)

откуда видно, что для открытого сосуда понятия весового и избыточного давлений совпадают:

p = p_в = γh (2-41)

для закрытого же сосуда давления p и p_в имеют разную величину:

p = p_в + (p₀ – p_a). (2-41')

Как видно, всего имеем пять различных давлений, обозначаемых через p_A, p, p_в, p_a и p₀ причем под p₀ условимся понимать абсолютное поверхностное давление.

Говоря далее о силе гидростатического давления P, будем различать:

1) силу абсолютного гидростатического давления P_A;

2) силу избыточного гидростатического давления (сверхатмосферного) P. Последнюю далее часто будем именовать просто силой гидростатического давления P (опуская слово «избыточного»).