Пьезометрическая высота, отвечающая избыточному давлению в точке.

Рассмотрим точку n (рис. 2-9); приключим к этой точке тонкую стеклянную трубку П открытого типа. В этой трубке горизонт жидкости, благодаря действию давления p_A в точке n, также поднимется на некоторую высоту h_изб. Однако h_изб будет меньше h_A (относящегося к точке n), так как в случае открытой трубки жидкость в ней будет встречать противодавление со стороны атмосферы. Рассматривая точку n, можем сказать, что:

а) со стороны жидкости в сосуде на точку n действует давление

p_A = p₀ + γh; (2-46)

б) со стороны жидкости в трубке на точку n действует давление

pa + γh_изб. (2-47)

Так как давления слева и справа на точку должны быть равными, то получаем:

pA = pa + γh_изб. (2-48)

откуда

hизб = =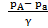

, (2-49)

где р - избыточное давление в точке n.

Величина h_изб называется пьезометрической высотой, отвечающей избыточному давлению в точке, или избыточной пьезометрической высотой или просто пьезометрической высотой. Как видно, пьезометрическая высота h_изб, в отличие от пьезометрической высоты h_A, выражает лишь разность давлений: p_A - p_a. Трубки П₀ и П называются пьезометрами соответственно закрытого и открытого типа.

Легко доказать следующие два положения:

1) разность высот стояния горизонтов жидкости в трубках П₀ и П всегда равна p_a/γ;

2) в случае открытого сосуда, когда p₀ = p_a, величина h_изб = р, где h - заглубление данной точки под уровнем жидкости в сосуде.

ВАКУУМ

Выше рассматривался случай, когда абсолютное давление в точке больше атмосферного. Обратимся теперь к случаю, когда p_A ‹ p_a. Положим, что таким давлением характеризуется точка m, показанная на рис. 2-10. Давление в точке т при условии p_A ‹ p_a можно измерить с помощью так называемого обратного пьезометра, или, что то же, вакуумметра, представляющего собой изогнутую трубку V.

Очевидно, горизонт жидкости в такой трубке опустится ниже точки т; заглубление точки т по отношению к горизонту жидкости в трубке V будет отрицательным (h_вак на рис. 2-10).

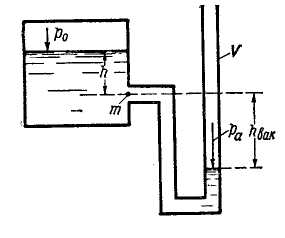
Рис. 2-10. Вакуум h_вак - вакуумметрическая высота или высота вакуума

Можно сказать, что:

а) давление в точке т со стороны жидкости в сосуде равно

p_A = p₀ + γh; (2-50)

б) давление в точке т со стороны жидкости в трубке V равно

(2-51)

Соединяя знаком равенства два приведенных выражения, получим:

p_A = p_a - γh_вак (2-52)

откуда

hизб =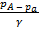

где р – избыточное давление в точке n (2-53)

Величину h_изб называют вакуумметрической высотой или высотой вакуума. Как видно, h_изб характеризует разность двух давлений: атмосферного и абсолютного давления в точке p_A - p_a. Именно эта разность, а не само давление, называется вакуумом (от латинского слова vacuum «пустота»). Можно сказать, что вакуум в данной точке жидкости есть недостаток давления в этой точке до атмосферного. Иногда вакуумом называют также состояние жидкости, когда давление в ней менее атмосферного. Величина вакуума может выражаться тремя способами:

1) единицами 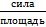, например, кН/м², т. е. кПа (или, например, кгс/см²);

2) единицами длины (единицами высоты) вертикального столба жидкости, характеризуемой определенной величиной γ;

3) в долях атмосферного давления (в обычных условиях вакуум не может быть больше того давления, которое развивает в данном месте атмосфера).

Если в данной точке вакуум равен, например, 4 м вод. ст., то это значит, что абсолютное давление в этой точке равно 6 м вод. ст.

В § 1-4, п. 6 было рассмотрено поднятие жидкости в капиллярной трубке К (см. рис. 1-5).

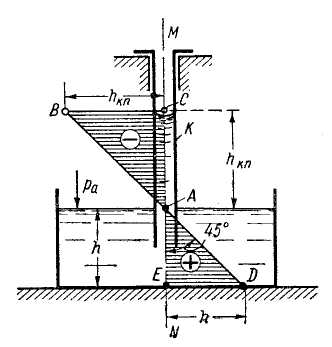
Рис. 2-11. Высота капиллярного поднятия /г_{к п} жидкости в трубке К Заштрихованы эпюры гидростатического, давления: положительного и отрицательного (по отношению к атмосферному давлению)

Не учитывая вовсе молекулярного давления, можем сказать, что в жидкости, находящейся в капиллярной зоне, должен иметь место вакуум. Эпюра изменения величины h_вак вдоль оси М - N капиллярной трубки К (рис. 2-11) выразится треугольником ABC: эпюра же избыточного давления

h_изб = =

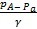
для линии АЕ представится треугольником ADE.

Поскольку в данном случае вакуум образуется за счет разности давлений плоской и вогнутой поверхностных пленок, то он, вообще говоря, может быть и больше одной атмосферы.