Деформированное состояние в точке. Геометрические уравнения и уравнения неразрывности

Происходящие при нагружении тела перемещения его точек можно задать при помощи совокупности трех функций (см. п.1.5): u (x, y, z), v (x, y, z) и w (x, y, z), определяющих перемещения вдоль коорди­натных осей x, y и z, соответственно. Достаточно просто можно показать, что деформации (линейные и угловые) выражаются через функции перемещений, (в случае малых перемещений, которые рассматриваются в сопротивлении материалов):

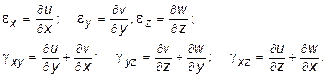(10.16)

где e_i - линейная деформация вдоль i-той оси координат, g_ij -уг­ловая деформация в плоскости i 0j (i , j = x, y, z) (см. рис. 10.1).

Правило знаков принимается следующее: для линейных дефор­маций - растяжению соответствует положительная деформация; для угловых деформаций положительное ее значение соответствует уменьшению прямого угла между положительными направлениями осей. По аналогии с напряженным состоянием, здесь также имеют­ся главные деформации и главные площадки деформирования, которые являются инвариантами, независящими от осей коорди­нат.

Принятая в механике деформируемого тела гипотеза о сплош­ности среды, выражающаяся, в частности, в том, что в одну и ту же точку пространства не могут придти две материальные точки, рав­но, как и не допускается разрывов среды, находит свое воплощение в уравнениях неразрывности деформаций. Как видно из (10.16), шесть компонентов деформаций выражаются через три функции перемещений - следовательно между ними существует определен­ная связь в виде:

;

;

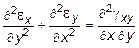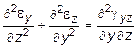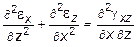; (10.17)

;

;

.

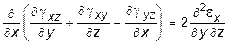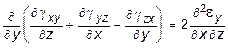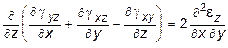Убедиться в верности (10.17) можно просто - достаточно под­ставить в них выражения (10.16). В случае плоской задачи, за исключением первого уравнения системы (10.17), остальные уравнения превращаются в тождество.

В заключение заметим, что в каждой точке среды деформируе­мого тела всегда существуют три взаимно перпендикулярные плос­кости, которые не испытывают сдвигов. Координатные оси, кото­рые образуют эти плоскости, называются главными осями деформируемого состояния.

Линейные деформации по главным осям называются глав­ными деформациями и нормируются в порядке e₁ > e₂ > e₃ с учетом их знака, причем знак “плюс” относится к тем деформаци­ям, которые вызваны в результате растяжения, и наоборот, знак “минус” относится к деформациям сжатия.

Заметим, что для изотропного тела, свойства которого не зави­сят от направлений координатных осей, главные оси напряжений и деформаций совпадают.