Возможные способы решения задач теории упругости

В общем случае искомыми величинами в задачах теории упру­гости являются функции перемещений, компоненты напряженного и деформированного состояний среды. Следовательно, в каждой точке тела подлежат определению 15 величин: три компоненты смещений - u, v и w; шесть компонент напряжений - s_x , s_y , s_z , t_xy , t_xz и t_yz ; шесть компонент деформаций - e_x , e_y , e_z , g_xy , g_xz , g_yz .

Очевидно, что для решения задачи в общем случае необходимо 15 уравнений, связывающих искомые величины, которые выполня­лись бы не только внутри заданного тела, но и на его границе.

Полученные выражения (10.2), (10.16), (10.18), (10.19) образуют такую систему. Для однозначного решения задачи необходимо задание условий на контуре тела - граничных условий. Эти условия могут быть заданы в виде заранее определенных компонент напря­жений (статические граничные условия) или компонент перемеще­ний (кинематические граничные условия) или же комбинации тех и других (смешанные граничные условия).

Если заданы граничные условия и требуется оценить напря­женно-деформированное состояние заданного тела, то такая задача называется прямой задачей теории упругости. Если же по задан­ным функциям напряженно-деформированное состояния рассмат­риваемого тела требуется найти граничные условия им соответству­ющие, то такая задача называется обратной задачей теории упру­гости.

Решение прямой задачи теории упругости можно вести разны­ми способами. Если в качестве неизвестных принять функции пе­ремещений - u, v и w, то полную система уравнений (10.2), (10.16), (10.18), (10.19) можно свести к следующим трем дифференциаль­ным уравнениям относительно этих функций:

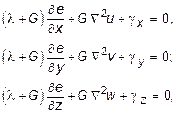(10.21)

где 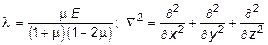- оператор Лапласа.

Уравнения (10.21) называются уравнениями Ляме. Граничные условия также необходимо выразить через перемещения. В итоге контурные напряжения запишутся через перемещения в следу­ющем виде:

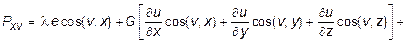
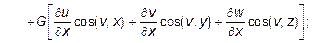
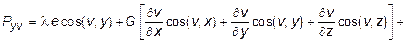
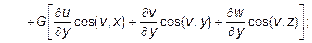(10.22)

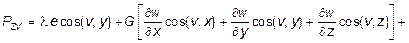
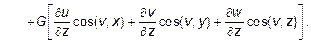
Если же в качестве неизвестных принять компоненты напря­женного состояния в произвольной точке тела - s_x , s_y , s_z , t_xy , t_xz и t_yz , то к уравнениям равновесия (10.2) нужно присоединить уравнения совместности деформаций (10.17) и закон Гука (10.18-10.19). В результате совместного рассмотрения такой системы диф­ференциальных уравнений получаются так называемые уравнения Бельтрами:

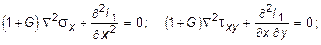
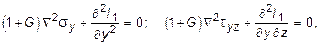(10.23)

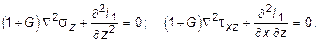
где I₁ - первый инвариант напряженного состояния в точке.

Произвольные постоянные, получаемые в результате интегри­рования уравнений (10.23), находятся при учете граничных усло­вий, выраженных в следующем виде:

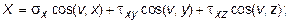
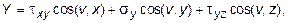
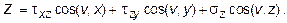
где X, Y, Z - компоненты полного напряжения на границе.